Rozwiążmy teraz kilka zadań, ilustrujących związki między własnościami funkcji a własnościami funkcji pochodnej.
Przykład 1.
Wyznacz przedziały monotoniczności funkcji f(x) i f ' (x) określonych w przedziale <-3,3>.
Jakie wartości w tym przedziale przyjmuje pochodna funkcji ?
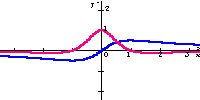
y = f(x)
y = f ' (x)
Analizując powyższy wykres odczytujemy:
Funkcja f jest
rosnąca w przedziale (-1;1); jej pochodna w tym przedziale jest dodatnia,
Funkcja f jest malejąca w przedziałach
(-3;-1), (1;3); .jej pochodna w tych przedziałach jest ujemna.
I rzeczywiście tak jest.
Można udowodnić, wykorzystując definicję pochodnej, że
zachodzi twierdzenie 1 i
twierdzenie 2. o znaku pochodnej funkcji rosnącej (malejącej).
Prawdziwe są również twierdzenia :
twierdzenie 3 i
twierdzenie 4 o monotoniczności funkcji, której pochodna jest dodatnia (ujemna).
Jednocześnie możemy odczytać z wykresu, że dana funkcja jest nieparzysta, zaś jej pochodna jest parzysta.
Ten fakt również można udowodnić.
Prawdziwe jest
twierdzenie 5 o pochodnej funkcji nieparzystej.
Popatrzmy na następny rysunek.
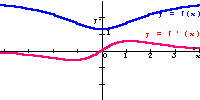Z tego wykresu odczytujemy, że:
w przedziale (0;3) funkcja jest rosnąca, jej pochodna
w tym przedziale jest dodatnia;
w przedziale (-3;0) funkcja jest malejąca,jej pochodna
w tym przedziale jest ujemna.
Potwierdzają się nasze obserwacje o związku monotoniczności funkcji ze znakiem pochodnej.
Jednocześnie możemy odczytać z wykresu, że dana funkcja jest parzysta, zaś jej pochodna jest
nieparzysta.
Ten fakt również można udowodnić.
Prawdziwe jest
twierdzenie 6 o pochodnej funkcji parzystej.
Zauważ, że jeżeli przedział <-3,3> zastąpimy innym przedziałem, nawet nieograniczonym, to omawiane własności funkcji zachowają się.
Przykład 2.
Korzystając z wykresów funkcji określ, czy mają one ekstrema.
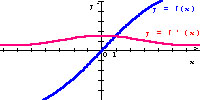f(x) = x + sin0,5x
Z wykresu wnioskujemy, że
pochodna nie ma miejsc zerowych,
więc dana funkcja nie ma ekstremów lokalnych.
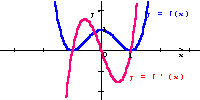f(x) = (x2-1)2
Obserwujemy, że pochodna ma dwa miejsca zerowe
x0=-1 i x1=1, w otoczeniu których nie zmienia znaku
(jest zawsze nieujemna).
Z wykresu odczytujemy, że funkcja nie ma ekstremów.
Fakty te można uogólnić (i udowodnić). Prawdziwe jest
twierdzenie 7 o ekstremum.
Przykład 3.
Wyznacz ekstrema funkcji y = f(x):
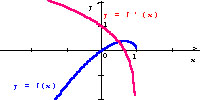Ta funkcja jest określona dla x € (-3;1>.
Pochodna ma jedno miejsce zerowe x0=0,6
(w przybliżeniu), w otoczeniu którego zmienia
wartości z dodatnich na ujemne.
Odczytujemy z wykresu, że funkcja osiąga w tym punkcie maksimum lokalne.
Przedział (-3,1> można zastąpić dowolnym przedziałem (a,1>, gdzie a € R .
Tak pięknie i gładko było w przypadkach funkcji różniczkowalnych . Zdarzają się jednak bardziej skomplikowane sytuacje.
Przykład 4.
Obserwując wykresy funkcji f(x) = | x | i jej pochodnej, wypowiedz się na temat różniczkowalności w zerze .
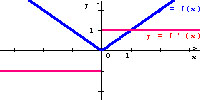
Zauważ, że
funkcja nie ma pochodnej w punkcie x = 0. dla x>0 pochodna jest funkcją stałą y = 1, dla x<0 pochodna jest funkcją stałą y = -1.
Ta funkcja nie jest różniczkowalna w punkcie x = 0, ale mimo to ma minimum w tym punkcie, ponieważ spełniona jest definicja minimum. Wartość, jaką przyjmuje nasza funkcja w x = 0 jest najmniejszą spośród wartości w sąsiedztwie zera (f(1) Ł 0 dla każdego x ą 0)
Przykład 5.
Zbadaj różniczkowalność funkcji f określającej pole przekroju
sześcianu o krawędzi 1 płaszczyzną przechodzącą przez krawędź podstawy i nachyloną do płaszczyzny podstawy pod kątem x,
x € (0, p/2).
Dla lepszego zrozumienia, narysuj sześcian i zaznacz przekrój płaszczyzną przechodzącą przez krawędź dolnej podstawy. Rozpatrywany przekrój jest prostokątem. Zaznacz kąt, jaki płaszczyzna przekroju tworzy z płaszczyzną podstawy i odpowiedni trójkąt prostokątny.
Pole f(x) przekroju wyraża się wzorem
1* 1/cosx dla 0 < x Łp/4,
1*1/cos( p/2 -x) dla x > p/4.
Popatrzmy na wykres tej funkcji i wykres jej pochodnej.
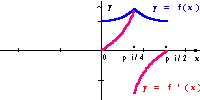
Funkcja f nie jest różniczkowalna w x = p /4.
Zwróć uwagę na to, jak potężnym narzędziem dysponujesz.
Rozwiązanie tego zadania każdą inną metodą byłoby o wiele bardziej
skomplikowane.
Mamy nadzieję, że po tej krótkiej pracy z tekstem świetnie rozwiążesz
Zadania do samodzielnego rozwiązania.