W tym paragrafie zajmiemy się wyznaczeniem powierzchni bryły obrotowej (tj. powstałej przez obrót pewnej
krzywej dookoła danej osi) w sposób odpowiadający naszej intuicji. Zacznijmy od prostych przykładów.
Powierzchnia boczna A walca o promieniu r i wysokości h daje się obliczyć ze wzoru
A = 2![]() rh,
możemy bowiem wyobrazić sobie, że celem jej obliczenia "rozcinamy" walec i rozwijamy go jako prostokąt.
rh,
możemy bowiem wyobrazić sobie, że celem jej obliczenia "rozcinamy" walec i rozwijamy go jako prostokąt.
![\includegraphics[width=12cm]{554-1.eps}](img838.gif)
W podobny sposób możemy poradzić sobie z powierzchniami bocznymi stożków; przecinając stożek o promieniu
podstawy r i pobocznicy l wzdłuż jednej z pobocznic, otrzymujemy po rozwinięciu pewien wycinek kołowy.
Wiemy, że pole powierzchni wycinka kołowego o kącie środkowym
![]() = 2
= 2![]() r/l wyraża się (jako procent
powierzchni koła) wzorem
r/l wyraża się (jako procent
powierzchni koła) wzorem
![]() l2
l2![]() , tak więc otrzymujemy
, tak więc otrzymujemy
![\includegraphics[width=12cm]{555-2.eps}](img841.gif)
Wiemy zatem w jaki sposób obliczać pola powierzchni brył obrotowych powstałych przez obroty odcinka wokół linii przechodzącej przez jeden z jego końców lub wokół linii do niego równoległej. W dalszym ciągu będziemy chcieli powtórzyć metodę użytą przy obliczaniu długości krzywej: spróbujemy aproksymować krzywą łamaną, a następnie powierzchnię obrotową inną powierzchnią, powstałą przez obrót aproksymującej łamanej. Każdy segment aproksymującej łamanej da po obrocie pewną wstęgę, której powierzchnię będziemy potrafili wyliczyć. W jaki sposób? Każda wstęga może być oczywiście rozpatrywana jako fragment pewnego stożka (lub walca).
Pole powierzchni takiej wstęgi o pobocznicy długości l, górnym promieniu r1 i dolnym r2 otrzymamy odejmując pola powierzchni bocznych dwóch stożków:
![\includegraphics[width=12cm]{555-3.eps}](img842.gif)
Wobec twierdzenia o trójkątach podobnych
Otrzymany w ten sposób wzór zastosujemy do obliczenia pola powierzchni bryły według pomysłu opisanego
powyżej. Rozważmy powierzchnię otrzymaną przez obrót krzywej y = f (x),
a ![]() x
x ![]() b, wokół osi x,
gdzie f jest funkcją o dodatnich wartościach i ciągłej pochodnej (w szczególności f jest ciągła).
Podzielmy odcinek [a, b] na n podprzedziałów o końcach wyznaczonych przez punkty
x0, x1,..., xn
i równej długości
b, wokół osi x,
gdzie f jest funkcją o dodatnich wartościach i ciągłej pochodnej (w szczególności f jest ciągła).
Podzielmy odcinek [a, b] na n podprzedziałów o końcach wyznaczonych przez punkty
x0, x1,..., xn
i równej długości ![]() x, w sposób podobny jak przy wyznaczaniu długości krzywej. Jeśli oznaczymy
yi = f (xi), to punkt
Pi(xi, yi) leży na rozpatrywanej krzywej. Fragment powierzchni leżący między
punktami xi-1 oraz xi możemy aproksymować biorąc odcinek
Pi-1Pi i obracając go dookoła osi
x.
x, w sposób podobny jak przy wyznaczaniu długości krzywej. Jeśli oznaczymy
yi = f (xi), to punkt
Pi(xi, yi) leży na rozpatrywanej krzywej. Fragment powierzchni leżący między
punktami xi-1 oraz xi możemy aproksymować biorąc odcinek
Pi-1Pi i obracając go dookoła osi
x.
![\includegraphics[width=12cm]{555-4.eps}](img845.gif)
Otrzymana w ten sposób wstęga będzie miała pobocznicę długości
l = | Pi-1Pi| and uśredniony
promień
r = ![]() (yi-1 + yi), tak więc pole jej powierzchni wyniesie
(yi-1 + yi), tak więc pole jej powierzchni wyniesie
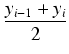 | Pi-1Pi|
| Pi-1Pi|
![$\displaystyle \sqrt{{1 + [f'(x_i^*)]^2}}$](img821.gif)
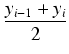 | Pi-1Pi|
| Pi-1Pi| ![$\displaystyle \sqrt{{1 + [f'(x_i^*)]^2}}$](img821.gif)
![$\displaystyle \sqrt{{1 + [f'(x_i^*)]^2}}$](img821.gif)
![$\displaystyle \sqrt{{1 + [f'(x_i^*)]^2}}$](img821.gif)
Przykład: Krzywa
y = ![]() ,
-1
,
-1 ![]() x
x ![]() 1, jest łukiem okręgu
x2 + y2 = 4.
Obliczyć pole powierzchni otrzymanej przez obrót tego łuku wokół osi x.
1, jest łukiem okręgu
x2 + y2 = 4.
Obliczyć pole powierzchni otrzymanej przez obrót tego łuku wokół osi x.
Obliczamy
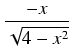
| S | = | 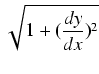 dx = dx = |
|
| = | 2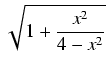 dx = dx = |
||
| = | 2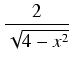 dx = dx = |
||
| = | 4 |