Co rozumiemy przez długość krzywej? W przypadku łamanej zamkniętej odpowiedź wydaje się stosunkowo prosta: długość takiej krzywej to suma długości składowych odcinków. W ogólnum przypadku definicja nieco się komplikuje. Będziemy starali się zdefiniować długości niektórych krzywych przbliżając dane krzywe łamanymi, a następnie przybliżając długość krzywej długością aproksymującej łamanej.
Niech C będzie łamaną opisaną równaniem y = f (x), gdzie f jest funkcją ciągła określoną dla
a ![]() x
x ![]() b.
Krzywą C przybliżamy za pomocą łamanej dzieląc przedział [a, b] na n podprzedziałów o końcach
x0, x1,..., xn i o równej długości
b.
Krzywą C przybliżamy za pomocą łamanej dzieląc przedział [a, b] na n podprzedziałów o końcach
x0, x1,..., xn i o równej długości ![]() x. Jeśli oznaczymy
yi = f (xi), to punkt
Pi(xi, yi) będzie leżał na krzywej C i łamana
P0, P1,..., Pn będzie przybliżeniem krzywej C.
x. Jeśli oznaczymy
yi = f (xi), to punkt
Pi(xi, yi) będzie leżał na krzywej C i łamana
P0, P1,..., Pn będzie przybliżeniem krzywej C.
![\includegraphics[width=12cm]{547-3.eps}](img816.gif)
Długość L krzywej C będzie zatem w przybliżeniu równa długości łamanej i przybliżenie to będzie tym lepsze, im większe n uwzględnimy w naszych rozważaniach.
![\includegraphics[width=12cm]{547-4.eps}](img817.gif)
Wobec tego możemy zdefiniować długość L krzywej C o równaniu y = f (x),
a ![]() x
x ![]() b
jako wartość graniczną
b
jako wartość graniczną
Niech
![]() yi = yi - yi-1. Wówczas
yi = yi - yi-1. Wówczas
| | Pi-1Pi| | = | ||
| = | ![$\displaystyle \sqrt{{(\Delta x)^2 + [f'(x_i^*) \Delta x_i^*]^2}}$](img820.gif) = = |
||
| = | ![$\displaystyle \sqrt{{1 + [f'(x_i^*)]^2}}$](img821.gif) |
||
| = | ![$\displaystyle \sqrt{{1 + [f'(x_i^*)]^2}}$](img821.gif) |
![$\displaystyle \sqrt{{1 + [f'(x_i^*)]^2}}$](img821.gif)
Przykład: Wyznaczyć długość łuku paraboli semikubicznej y2 = x3 pomiędzy punktami (1, 1) oraz (4, 8).
Łatwo przekonujemy się, że interesuje nas tylko ten fragment krzywej, dla której y jest dodatnie. Zatem
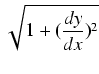 dx =
dx = 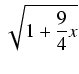 dx.
dx.
| L | = | ||
| = | |||
| = |