


Next: Długość krzywej
Up: Rachunek całkowy
Previous: Objętości brył wyrażone poprzez
W mowie potocznej przez termin "praca" rozumiemy ogół wysiłku potrzebny do wykonania określonego zadania.
Odpowiada to w pewnym sensie fizycznemu terminowi "pracy", opartemy na definicji siły. Intuicyjnie
możemy sobie wyobrazić, że do wykonania czynności takich jak przesunięcie książki na stole, podniesienie
jakiegoś przedmiotu z podłogi (i przeciwdziałanie tym samym grawitacji) wymaga określonej siły.
Ogólnie, gdy dany obiekt przesuwamy wzdłuż linii prostej opisanej równaniem s(t), to siła działająca
na dany obiekt określona jest - w myśl II Zasady Dynamiki Newtona - za pomocą wzoru:
F =
m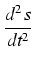
,
gdzie m oznacza masę danego obiektu. Ponieważ jednostką masy jest 1 kg, jednostką przesunięcia jest 1 m,
a jednostką siły jest 1 N, więc siła 1 N działająca na ciało o masie 1 kg skutkuje przyspieszeniem 1 m/s2.
W przypadku, gdy przyspieszenie utrzymuje się na stałym poziomie, działająca na obiekt siła również będzie stała.
W takiej sytuacji definiujemy pracę jako iloczyn siły i przesunięcia:
W = Fd.
Gdy siła mierzona jest w niutonach a przesunięcie w metrach, to za jednostkę pracy przyjmujemy niutonometry, lub inaczej dżule. Zatem przesuwając obiekt z siłą 1 N na odległość 1 m wykonujemy pracę 1 J; inaczej, praca 1 J to praca
potrzebna do przesunięcia ciała o masie 1 kg na odległość 1 m z przyspieszeniem 1 m/s2.
Powyższe równanie - znane ze szkoły podstawowej - opisuje sytuację, w której obiekt przemieszczany jest ze stałym
przyspieszeniem; oczywiście o wiele ciekawszy jest przypadek, w którym przyspieszenie (a więc i siła na obiekt działająca) zmienia się w czasie. Przypuśćmy, że obiekt porusza się wzdłuż osi x w kierunku dodatnim począwsz od punktu
x = a, a na punkcie x = b skończywszy. Załóżmy też, że w danym punkcie x na obiekt działa siła f (x), gdzie f jest
pewną funkcją ciągłą. Podzielmy odcinek [a, b] na n podprzedziałów o równej długości 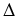 x, których końce wyznaczają
punkty
x0, x1,..., xn. Z każdego podprzedziału wybierzmy po jednym punkcie próbkującym
xi*
x, których końce wyznaczają
punkty
x0, x1,..., xn. Z każdego podprzedziału wybierzmy po jednym punkcie próbkującym
xi* 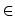 [xi-1, xi].
Siła działająca na obiekt w tym punkcie wyniesie f (xi*). Gdy n będzie odpowiednio duże, wówczas długość
[xi-1, xi].
Siła działająca na obiekt w tym punkcie wyniesie f (xi*). Gdy n będzie odpowiednio duże, wówczas długość 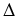 x
będzie stosnkowo mała i - ponieważ f jest funkcją ciągłą - wartości f nie zmieniają się aż tak bardzo na przedziale
[xi-1, xi]. Możemy więc założyć, że na tak krótkim przedziale f jest prawie funkcją stałą. Wobec tego praca
potrzebna na przesunięcie obiektu z punktu xi-1 do xi wyniesie w przybliżeniu
x
będzie stosnkowo mała i - ponieważ f jest funkcją ciągłą - wartości f nie zmieniają się aż tak bardzo na przedziale
[xi-1, xi]. Możemy więc założyć, że na tak krótkim przedziale f jest prawie funkcją stałą. Wobec tego praca
potrzebna na przesunięcie obiektu z punktu xi-1 do xi wyniesie w przybliżeniu
Wi 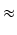 f
f (
xi*)
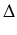 x
x.
Wobec tego całkowita praca wykonana przy przesuwaniu obiektu z punktu a do punktu b równa jest w przybliżeniu
Jasne jest, że przybliżenie jest tym lepsze, im n jest większe. Wobec tego możemy zdefiniować pracę wykonaną przy
przesuwaniu obiektu z a do b jako:
Przykład: Gdy cząsteczka znajduje się w odległości x od początku układu współrzędnych, siła działająca na nią
opisuje się równaniem
f (x) = x2 + 2x. Jaka praca wykonywana jest podczas przemieszczenia się cząsteczki od punktu
x = 1 do punktu x = 3?
Zgodnie z przeprowadzoną powyżej dyskusją:
W =
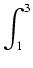 x2
x2 +2
xdx = [
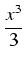
+
x2]|
13 =
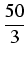
.
Przykład: Aby rozciągnąc sprężynę ze stanu spoczynku, w którym jej długośc wynosi 10 cm, do długości 15 cm,
potrzebna jest siła 40 N. Ile pracy potrzeba na dalsze rozciągnięcie sprężyny od 15 cm do 18 cm?
Zgodnie z prawem Hooke'a siła potrzebna do utrzymania rozciągniętej sprężyny na długości x jednostek od stanu
spoczynku jest proporcjonalna do długości x:
F(x) = kx.
Współczynnik k zwany jest stałą sprężystości. Gdy rozciągniemy sprężynę ze stanu spoczynku 10 cm do
długości 15 cm, różnica x wyniesie
x = 5 = 0, 05 m. Oznacza to, że
F(0, 05) = 40 N, a więc
0, 05k = 40,
skąd znajdujemy k = 800. Tym samym stała sprężystości rozważanej sprężyny wynosi 800 i równanie siły rozciągającej
przybiera postać
F(x) = 800x.
Tym samym praca wykonana przy dalszym rozciąganiu sprężyny od 15 cm do 18 cm wynosić będzie
| W |
= |
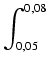 800xdx = [800 800xdx = [800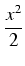 ]|0, 050, 08 = ]|0, 050, 08 = |
|
| |
= |
400[(0, 08)2 - (0, 05)2] = 1, 56J |
|
Przykład: Zbiornik wody w kształcie odwróconego stożka o okrągłej podstawie promienia 4 m i wysokości 10 m wypełniony jest wodą do wysokości 8 m. Wyznaczyć pracę potrzebną do opróżnienia zbiornika, jeżeli pompa umieszczona jest na jego szczycie.
Poziom wody w zbiorniku podczas pompowania zmieniać się będzie od 2 m do 10 m.
Podzielmy zatem odcinek [2, 10] na n podprzedziałów, których końce wyznaczone są przez punkty
x0, x1,..., xn
i wybierzmy punkty próbkujące xi*, po jednym z każdego podprzedziału. Tym samym podzieliliśmy wodę w zbiorniku na n warstw. Warstwa i może być przybliżona za pomocą walca o promieniu ri i wysokości  x.
Wielkość ri możemy łatwo obliczyć posługując się trójkątami podobnymi:
x.
Wielkość ri możemy łatwo obliczyć posługując się trójkątami podobnymi:
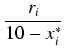
=
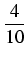
,
skąd
ri =
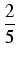
(10 -
xi*).
Wobec tego przybliżona objętość wody w i-tej warstwie równa się
i ponieważ gęstość wody 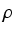 wynosi 1000 kg/m3, jej masa równa jest w przybliżeniu
wynosi 1000 kg/m3, jej masa równa jest w przybliżeniu
mi 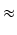
1000
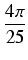
(10 -
xi*)
2 x
x = 160
(10 -
xi*)
2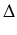 x
x.
Siła potrzebna na wypompowanie takiej warstwy wody musi przezwyciężyć siłę grawitacyjną, a więc równa jest
| Fi |
= |
mig 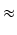 (9, 81)160 (9, 81)160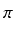 (10 - xi*)2 (10 - xi*)2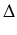 x x 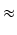 |
|
| |
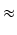 |
1570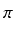 (10 - xi*)2 (10 - xi*)2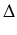 x x |
|
Każda warstwa wody musi zostać wypompowana na wysokość w przybliżeniu równą xi*. Tak więc praca Wi
wykonana podczas pompowania wynosi w przybliżeniu
Wi 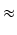 Fixi*
Fixi* 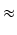
1570
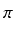 xi*
xi*(10 -
xi*)
2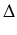 x
x.
Aby obliczyć całkowitą pracę wykonaną podczas pompowania musimy dodać do siebie wszystkie prace wykonane
przy pompowaniu kolejnych warstw, a następnie zwiększyć liczbę warstw występujących w obliczeniach, aby uczynić je bardziej dokładne. W ten sposób otrzymujemy następującą całkę do policzenia:
| W |
= |
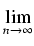 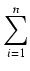 1570 1570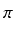 xi*(10 - xi*)2 xi*(10 - xi*)2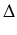 x = x = 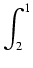 01570 01570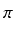 x(10 - x)2dx = x(10 - x)2dx = |
|
| |
= |
1570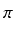 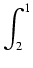 0(100x - 20x2 + x3)dx = 1570 0(100x - 20x2 + x3)dx = 1570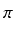 [50x2 - [50x2 - 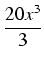 + + 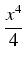 ]|210 = ]|210 = |
|
| |
= |
1570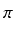 ( (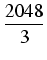 ) ) 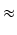 3, 4 . 106J 3, 4 . 106J |
|



Next: Długość krzywej
Up: Rachunek całkowy
Previous: Objętości brył wyrażone poprzez
Pawel Gladki
2006-01-30
![]() x, których końce wyznaczają
punkty
x0, x1,..., xn. Z każdego podprzedziału wybierzmy po jednym punkcie próbkującym
xi*
x, których końce wyznaczają
punkty
x0, x1,..., xn. Z każdego podprzedziału wybierzmy po jednym punkcie próbkującym
xi* ![]() [xi-1, xi].
Siła działająca na obiekt w tym punkcie wyniesie f (xi*). Gdy n będzie odpowiednio duże, wówczas długość
[xi-1, xi].
Siła działająca na obiekt w tym punkcie wyniesie f (xi*). Gdy n będzie odpowiednio duże, wówczas długość ![]() x
będzie stosnkowo mała i - ponieważ f jest funkcją ciągłą - wartości f nie zmieniają się aż tak bardzo na przedziale
[xi-1, xi]. Możemy więc założyć, że na tak krótkim przedziale f jest prawie funkcją stałą. Wobec tego praca
potrzebna na przesunięcie obiektu z punktu xi-1 do xi wyniesie w przybliżeniu
x
będzie stosnkowo mała i - ponieważ f jest funkcją ciągłą - wartości f nie zmieniają się aż tak bardzo na przedziale
[xi-1, xi]. Możemy więc założyć, że na tak krótkim przedziale f jest prawie funkcją stałą. Wobec tego praca
potrzebna na przesunięcie obiektu z punktu xi-1 do xi wyniesie w przybliżeniu
![\includegraphics[width=12cm]{462-3.eps}](img806.gif)
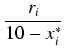 =
= ![\includegraphics[width=12cm]{462-4.eps}](img810.gif)