![\includegraphics[width=12cm]{455-1.eps}](img790.gif)
Niektóre zadania polegające na znalezieniu objętości danej bryły moga okazać się bardzo trudne w przypadku, gdy będziemy próbowali rozwiązać je metodami podanymi w poprzednim paragrafie. Przykładowo, rozważmy bryłę powstałą przez obrót obszaru ograniczonego krzywymi y = 2x2 - x3 oraz y = 0 wokół osi y.
![\includegraphics[width=12cm]{455-1.eps}](img790.gif)
Cięcia prostopadłe do osi y dają w rezultacie pierścienie, chcąc jednak obliczyć promienie wewnętrzny i zewnętrzny danego pierścienia napotykamy na problem rozwiązania równania trzeciego stopnia y = 2x2 - x3 dla niewiadomej x, gdzie y jest parametrem. Nie jest to możliwe do osiągnięcia gdy dysponujemy tylko środkami dostępnymi uczniom szkoły średniej.
W taki przypadkach pomocne może okazać się zdefiniowanie objętości za pomocą pierścieni cylindrycznych.
![\includegraphics[width=12cm]{455-2.eps}](img791.gif)
Chcąc obliczyć objętość V pierścienia cylindrycznego o promieniu wewnętrznym r1 i zewnętrznym r2
oraz wysokości h, odejmujemy objętość V1 walca o wysokości h i promieniu r1 od objętości V2
walca o wysokości h i promieniu r2:
| V | = | V2 - V1 = | |
| = | |||
| = | |||
| = | 2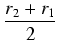 h(r2 - r1) h(r2 - r1) |
Niech teraz S będzie bryłą powstałą przez obrót wokół osi y obszaru ograniczonego krzywymi y = f (x),
gdzie
f (x) ![]() 0 oraz y = 0, x = a i x = b dla
b > a
0 oraz y = 0, x = a i x = b dla
b > a ![]() 0.
0.
![\includegraphics[width=12cm]{455-3.eps}](img794.gif)
Dzielimy przedział [a, b] na n podprzedziałów
Ii = [xi-1, xi] o równej długości ![]() x.
Niech
x.
Niech
![]() oznacza środek przedziału Ii. Jeżeli obrócimy prostokąt o podstawie Ii
i wysokości
f (
oznacza środek przedziału Ii. Jeżeli obrócimy prostokąt o podstawie Ii
i wysokości
f (![]() ) wokół osi y, to w rezultacie otrzymamy pierścień cylindryczny
o uśrednionym promieniu
) wokół osi y, to w rezultacie otrzymamy pierścień cylindryczny
o uśrednionym promieniu
![]() , wysokości
f (
, wysokości
f (![]() ) oraz grubości
) oraz grubości ![]() x.
x.
![\includegraphics[width=12cm]{456-4.eps}](img796.gif)
Objętość tak otrzymanego pierścienia wyniesie zatem
Przykład: Obliczyć objętość bryły S otrzymanej przez obrót wokół osi y obszaru ograniczonego krzywymi y = 2x2 - x3 oraz y = 0.
Widzimy, że składowy pierścień cylindryczny użyty do obliczenia objętości ma w tym przypadku
promień x, średni obwód 2![]() x i wysokość
f (x) = 2x2 - x3.
x i wysokość
f (x) = 2x2 - x3.
![\includegraphics[width=12cm]{457-6.eps}](img798.gif)
Wobec tego objętość obliczona za pomocą pierścieni cylindrycznych wynosi
| V | = | ||
| = | 2 |
Używając metody pierścieni cylindrycznych możemy też obliczać objętości brył powstałych przez obroty wokół osi x. Czytelnik zechce samodzielnie przeanalizować taką sytuację.