Powierzchnie ograniczone krzywymi

W poprzednich paragrafach zdefiniowaliśmy i podaliśmy metody obliczania pól pod wykresami funkcji. Obecnie uogólnimy nieco osiągnięte rezultaty i użyjemy całek oznaczonych do obliczania pól powierzchni ograniczonych wykresami dwóch funkcji.

Rozważmy obszar S leżący pomiędzy wykresami funkcji y = f (x) oraz y = g(x) oraz pionowymi liniami x = a i x = b, gdzie f i g są funkcjami ciągłymi oraz f (x) $\geq$ g(x) dla x $\in$ [a, b].

Tak jak poprzednio, podzielmy obszar S na n pasków o równej szerokości, a następnie przybliżmy i-ty pasek prostokątem o podstawie $\Delta$x i wysokości f (x_i^*) - g(x_i^*).

Suma Riemanna

$$\sum_{{i=1}}^{n}$$[f (x_i^*) - g(x_i^*)]$$\Delta$$x

jest przybliżeniem wielkości, którą intuicyjnie rozpoznajemy jako pole powierzchni S. Przybliżenie to staje się bardziej dokładne, gdy n $\rightarrow$ $\infty$. Możemy wobec tego zdefiniować pole A obszaru S jako granicę sum pól powierzchni przybliżających prostokątów:

A = $$\lim_{{n \rightarrow \infty}}^{}$$$$\sum_{{i=1}}^{n}$$[f (x_i^*) - g(x_i^*)]$$\Delta$$x.

Z łatwością potrafimy rozpoznać występującą w powyższym wzorze sumę jako całkę z funkcji f - g. Wobec tego możemy napisać, że pole A obszaru ograniczonego krzywymi y = f (x), y = g(x) i pionowymi liniami x = a, x = b, gdzie f i g są funkcjami ciągłymi oraz f (x) $\geq$ g(x) dla x $\in$ [a, b] równe jest

A = $$\int_{a}^{b}$$[f (x) - g(x)]dx

Przykład: Wyznaczyć pole obszaru ograniczonego wykresami parabol y = x² oraz y = 2x - x².

W pierwszej kolejności wyznaczamy punkty przecięcia parabol rozwiązując układ równań utworzony przez równania parabol. Otrzymujemy x² = 2x - x², czyli 2x² - 2x = 0, skąd dostajemy 2x(x - 1) = 0, a więc x = 0 lub x = 1. Tym samym punktami przecięcia się parabol będą (0, 0) oraz (1, 1).

Widzimy, że górna i dolna parabola mają równania, odpowiednio

y_T = 2x - x² oraz y_B = x².

Pole powierzchni przybliżającego prostokąta równe jest zatem

(y_T - y_B)$$\Delta$$x = (2x - x² - x²)$$\Delta$$x

i omawiany obszar leży między prostymi x = 0 i x = 1. Zatem całkowite pole powierzchni równe jest

$$\int_{0}^{1} \int_{0}^{1}$$ A =

$${\frac{{x^2}}{{2}}} {\frac{{x^3}}{{3}}}$$ =

$${\frac{{1}}{{2}}} {\frac{{1}}{{3}}} {\frac{{1}}{{3}}}$$ =

Jeżeli musimy policzyć pole powierzchni ograniczone krzywymi y = f (x) i y = g(x), gdzie f (x) $\geq$ g(x) dla pewnych wartości x, ale f (x) $\leq$ g(x) dla innych, to wówczas możemy podzielić obszar S na kilka podobszarów S₁, S₂,... o polach A₁, A₂,....

Pole obszaru S możemy wtedy zdefiniować jako sumę pól obszarów S₁, S₂,..., czyli A = A₁ + A₂ +.... Ponieważ

| f (x) - g(x)| = $$\left\{\vphantom{ \begin{array}{ll} f(x) - g(x) & \mbox{ gdy } f(x) \geq g(x) \\ g(x) - f(x) & \mbox{ gdy } g(x) \geq f(x) \end{array} }\right.$$$$\begin{array}{ll} f(x) - g(x) & \mbox{ gdy } f(x) \geq g(x) \\ g(x) - f(x) & \mbox{ gdy } g(x) \geq f(x) \end{array}$$

otrzymujemy następujący wzór na pole A powierzchni obszaru ograniczonego krzywymi y = f (x) i y = g(x) oraz liniami pionowymi x = i x = b:

A = $$\int_{a}^{b}$$| f (x) - g(x)| dx

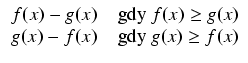
Przykład: Obliczyć pole obszaru ograniczonego krzywymi y = sin x oraz y = cos x pomiędzy x = 0 oraz x = ${\frac{{\pi}}{{2}}}$.

Punkt przecięcia się krzywych ma współrzędną x równą x = ${\frac{{\pi}}{{4}}}$ (jako że 0 $\leq$ x $\leq$ ${\frac{{\pi}}{{2}}}$). Zauważmy, że cos x $\geq$ sin x dla 0 $\leq$ x $\leq$ ${\frac{{\pi}}{{4}}}$ ale sin x $\geq$ cos x dla ${\frac{{\pi}}{{4}}}$ $\leq$ x $\leq$ ${\frac{{\pi}}{{2}}}$. Tym samym szukane pole wynosi:

$$\int_{0}^{{\frac{\pi}{2}}}$$ A =

$$\int_{0}^{{\frac{\pi}{4}}} \int_{{\frac{\pi}{4}}}^{{\frac{\pi}{2}}}$$ =

$${\frac{{\pi}}{{4}}} {\frac{{\pi}}{{4}}} {\frac{{\pi}}{{2}}}$$ =

$${\frac{{1}}{{\sqrt{2}}}} {\frac{{1}}{{\sqrt{2}}}} {\frac{{1}}{{\sqrt{2}}}} {\frac{{1}}{{\sqrt{2}}}}$$ =

$$\sqrt{{2}}$$ =

Niektóre pola łatwiej jest policzyć traktując x jako funkcję y. Jeżeli dany obszar ograniczony jest krzywymi x = f (y), x = g(y), y = c oraz y = d, gdzie f i g są funkcjami ciągłymi oraz f (y) $\geq$ g(y) dla x $\leq$ y $\leq$ d, to jego pole wyraża się wzorem

A = $$\int_{c}^{d}$$[f (y) - g(y)].

Przykład: Obliczyć pole obszaru ograniczonego prostą y = x - 1 i parabolą y² = 2x + 6.

Rozwiązując odpowiedni układ równan przekonujemy się, że krzywe przecinają się w puntach (- 1, - 2) oraz (5, 4). Przekształcamy równanie paraboli tak, aby było funkcją zmiennej y. Tym samym nasz obszar ograniczony jest z lewej i z prawej strony krzywymi

x_L = $${\frac{{1}}{{2}}}$$y² -3 oraz x_R = y + 1.

Przeprowadzamy całkowanie od y = - 2 do y = 4:

$$\int_{{-2}}^{4}$$ A =

$$\int_{{-2}}^{4} {\frac{{1}}{{2}}}$$ =

$$\int_{{-2}}^{4} {\frac{{1}}{{2}}}$$ =

$${\frac{{1}}{{2}}} {\frac{{y^3}}{{3}}} {\frac{{y^2}}{{2}}}$$ =

$${\frac{{1}}{{6}}} {\frac{{4}}{{3}}}$$ =