


Next: Powierzchnie ograniczone krzywymi
Up: Rachunek całkowy
Previous: Podstawowe twierdzenie rachunku całkowego
Przy obliczaniu całek nieoznaczonych dość częstym trickiem jest całkowanie przez podstawienie.
Korzystając ze wzory Newtona-Leibniza możemy tę metodę wykorzystać także w obliczaniu całek oznaczonych.
Przykładowo, chcąc obliczyć całkę oznaczoną
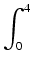
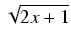 dx
dx
możemy najpierw policzyć całkę nieoznaczoną
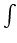
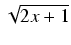 dx, a następnie skorzystać ze wzoru
Newtona-Leibniza. W obliczaniu tej całki konieczne jest zastosowania prostego podstawienia u = 2x + 1.
Wówczas du = 2dx i otrzymujemy
dx, a następnie skorzystać ze wzoru
Newtona-Leibniza. W obliczaniu tej całki konieczne jest zastosowania prostego podstawienia u = 2x + 1.
Wówczas du = 2dx i otrzymujemy
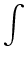
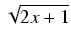 dx
dx =
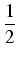
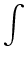
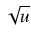 du
du =
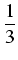 u
u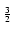
+
C =
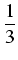
(2
x + 1)
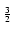
+
C
i na podstawie wzoru Leibniza
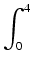
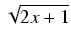 dx
dx =
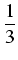
(2
x + 1)
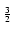
|
04 =
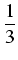
9
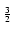
-
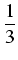
1
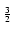
=
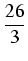
.
Sposób ten jest jak najbardziej poprawny, ale prowadzi do niebezpiecznych przyzwyczajeń, które okazują
się szczególnie bolesne, gdy Czytelnik zacznie studiować teorię całek wielu zmiennych. Dlatego lepszym
pomysłem jest dokonywanie zmian granic całkowania podczas procesu znajdowania całki nieoznaczonej
- do tego służy nam twierdzenie o zmianie zmiennych w całce oznaczonej.
Twierdzenie: Jeśli pochodna g' jest ciągła na przedziale [a, b] oraz f jest ciągła
w całym zbiorze wartości funkcji u = g(x),
a 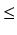 x
x 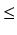 b, to wówczas
b, to wówczas
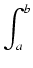 f
f (
g(
x))
g'(
x)
dx =
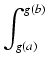 f
f (
u)
du.
Dowód: Niech F będzie całką nieoznaczoną z funkcji f. Wówczas F(g(x)) staje się
całką nieoznaczoną z funkcji
f (g(x))g'(x), a więc wobec wzoru Newtona-Leibniza otrzymujemy
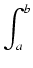 f
f (
g(
x))
g'(
x)
dx =
F(
g(
x))|
ab =
F(
g(
b)) -
F(
g(
a)).
Stosując wzór Newtona-Leibniza po raz drugi dostajemy:
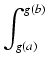 f
f (
u)
du =
F(
u)|
g(a)g(b) =
F(
g(
b)) -
F(
g(
a)).
Przykład: Obliczymy jeszcze raz całkę
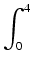
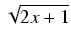 dx
dx,
tym razem stosując powyższe twierdzenie.
Jeśli u = 2x + 1, to du = 2dx. Ponadto, gdy x = 0, to u = 1 - a gdy x = 4, to u = 9. Zatem
Stosując twierdzenie o zamianie zmiennych w całce oznaczonej udowodnimy następujące twierdzenie,
pozwalające łatwo obliczać całki z funkcji parzystych lub nieparzystych określonych na symetrycznych
dziedzinach.
Twierdzenie: Załóżmy, że f jest ciągła na przedziale [a, b].
- (a)
- Jeśli f jest parzysta, tj.
f (- x) = f (x), to wówczas
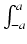 f (x)dx = 2
f (x)dx = 2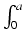 f (x)dx.
f (x)dx.
- (b)
- Jeśli f jest nieparzysta, tj.
f (- x) = - f (x), to wówczas
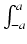 f (x)dx = 0.
f (x)dx = 0.
Dowód: Rozbijamy nasze całki na dwie części:
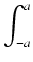 f
f (
x)
dx =
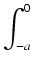 f
f (
x)
dx +
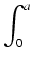 f
f (
x)
dx = -
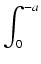 f
f (
x)
dx +
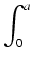 f
f (
x)
dx.
W pierwszej całce po prawej stronie stosujemy podstawienie u = - x. Wówczas du = - dx i gdy x = - a, to
u = a. A zatem
-
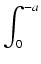 f
f (
x)
dx = -
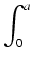 f
f (-
u)(-
du) =
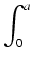 f
f (-
u)
du
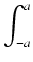 f
f (
x)
dx =
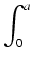 f
f (-
u)
du +
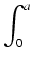 f
f (
x)
dx.
Gdy f jest parzysta, to
f (- u) = f (u) i otrzymujemy
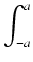 f
f (
x)
dx =
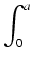 f
f (
u)
du +
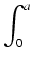 f
f (
x)
dx = 2
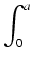 f
f (
x)
dx.
Gdy f jest nieparzysta, to
f (- u) = - f (u) i otrzymujemy
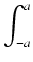 f
f (
x)
dx = -
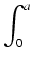 f
f (
u)
du +
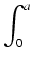 f
f (
x)
dx = 0.
Przykład: Obliczyć całkę
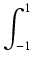
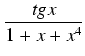 dx
dx.
Stosując powyższe twierdzenie zauważamy, że skoro funkcja
f (x) = 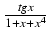 jest nieparzysta,
to rozpatrywana całka równa jest zeru.
jest nieparzysta,
to rozpatrywana całka równa jest zeru.



Next: Powierzchnie ograniczone krzywymi
Up: Rachunek całkowy
Previous: Podstawowe twierdzenie rachunku całkowego
Pawel Gladki
2006-01-30
![]() x
x ![]() b, to wówczas
b, to wówczas
![\includegraphics[width=12cm]{420-4.eps}](img744.gif)
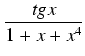 dx.
dx.