


Next: Podstawienia w całkach oznaczonych
Up: Rachunek całkowy
Previous: Całka oznaczona
Nazwa "podstawowe twierdzenie rachunku całkowego" nie jest zbyt adekwatna - powinna brzmieć raczej
"podstawowe twierdzenie rachunku całkowego i różniczkowego", opisuje bowiem związek między tymi dwoma
działami analizy matematycznej. Przypomnijmy, że rachunek różniczkowy "narodził się" z rozważań dotyczących
problemu opisania stycznych do krzywych - z kolei rachunek całkowy wziął swój początek z prób opisu pól
figur ograniczonych wykresami funkcji. Związek między tymi dwoma zagadnieniami został zauważony przez
Isaaca Barrowa (1630-1677), jednego z nauczycieli Newtona, zaś sformalizowany i szczegółowo opisany później
przez Newtona i Leibniza.
Twierdzenie składa się z dwóch części - choć w zastosowaniach głównie korzystamy z drugiej z nich,
to kluczem do zrozumienia dowodu jest pierwsza część. Opisuje ona zachowanie funkcji postaci:
g(
x) =
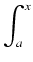 f
f (
t)
dt,
gdzie f jest funkcją ciągłą na przedziale [a, b], zaś x przybiera wartości pomiędzy a i b.
Funkcja g zależy w tym wypadku tylko od x, który jest górną granicą całkowania funkcji f.
Jeśli x jest ustalona liczbą, to wtedy
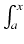 f (t)dt jest liczbą rzeczywistą - wszelako gdy x
się zmienia, zmienia się też wartość całki
f (t)dt jest liczbą rzeczywistą - wszelako gdy x
się zmienia, zmienia się też wartość całki
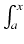 f (t)dt, która tym samym staje się funkcją zmiennej
x. W przypadku gdy f przyjmuje tylko dodatnie wartości, funkcję g(x) możemy interpretować
jako pole pod wykresem f od punktu a począwszy, a na punkcie x skończywszy (a więc "dotychczasowe"
pole "rozciągającej się" figury).
f (t)dt, która tym samym staje się funkcją zmiennej
x. W przypadku gdy f przyjmuje tylko dodatnie wartości, funkcję g(x) możemy interpretować
jako pole pod wykresem f od punktu a począwszy, a na punkcie x skończywszy (a więc "dotychczasowe"
pole "rozciągającej się" figury).
Co możemy powiedzieć o pochodnej takiej funkcji? Załóżmy, że f jest funkcją ciągłą taką, że
f (x) 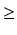 0,
a więc
g(x) =
0,
a więc
g(x) = 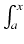 f (t)dt reprezentuje pole pod wykresem f od punktu a do punktu x. Aby obliczyć
pochodną funkcji g z definicji wpierw zauważmy, że dla h > 0 różnica
g(x + h) - g(x) jest różnicą pól figur,
a więc polem pod wykresem funkcji f od punktu x do x + h.
f (t)dt reprezentuje pole pod wykresem f od punktu a do punktu x. Aby obliczyć
pochodną funkcji g z definicji wpierw zauważmy, że dla h > 0 różnica
g(x + h) - g(x) jest różnicą pól figur,
a więc polem pod wykresem funkcji f od punktu x do x + h.
Dla małych wartości h wartość ta równa się
w przybliżeniu polu prostokąta o wysokości f (x) i szerokości h:
g(
x +
h) -
g(
x)
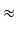 hf
hf (
x),
a zatem
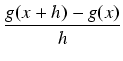
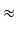 f
f (
x).
Tak więc intuicyjnie możemy zapisać, że
g'(
x) =
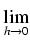
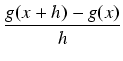
=
f (
x).
Twierdzenie to zapiszemy teraz dokładnie i przeprowadzimy formalny dowód.
Twierdzenie (podstawowe twierdzenie rachunku całkowego): Jeśli f jest funkcją ciągła na przedziale
[a, b], to funkcja g zdefiniowana wzorem
jest ciągła na przedziale [a, b] i różniczkowalna na przedziale (a, b) oraz zachodzi wzór
g'(x) = f (x).
Dowód: Jeśli x oraz x + h są liczbami z przedziału (a, b), to:
| g(x + h) - g(x) |
= |
 f (t)dt - f (t)dt - 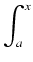 f (t)dt = f (t)dt = |
|
| |
= |
(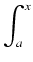 f (t)dt + f (t)dt +  f (t)dt) - f (t)dt) - 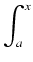 f (t)dt = f (t)dt = |
|
| |
= |
 f (t)dt, f (t)dt, |
|
a więc dla h 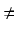 0 dostajemy
Załóżmy dalej, że h > 0. Ponieważ f jest ciągła na przedziale [x, x + h], więc dla pewnych liczb
u i v z tego przedziału f (u) = m oraz f (v) = M, gdzie m i M są, odpowiednio, najmniejszą
i największą wartością funkcji f na przedziale [x, x + h].
Zatem na mocy jednej z podstawowych własności
całek dostajemy:
czyli
Ponieważ h > 0, więc po podzieleniu wszystkich stron nierówności przez h dostaniemy
co po połączeniu z wcześniej otrzymanym wzorem daje
W podobny sposób możemy dowieśc podobnej nierówności w przypadku, gdy h < 0 - ta część dowodu pozostawiona
jest Czytelnikowi jako ćwiczenie. Niech teraz
h
0 dostajemy
Załóżmy dalej, że h > 0. Ponieważ f jest ciągła na przedziale [x, x + h], więc dla pewnych liczb
u i v z tego przedziału f (u) = m oraz f (v) = M, gdzie m i M są, odpowiednio, najmniejszą
i największą wartością funkcji f na przedziale [x, x + h].
Zatem na mocy jednej z podstawowych własności
całek dostajemy:
czyli
Ponieważ h > 0, więc po podzieleniu wszystkich stron nierówności przez h dostaniemy
co po połączeniu z wcześniej otrzymanym wzorem daje
W podobny sposób możemy dowieśc podobnej nierówności w przypadku, gdy h < 0 - ta część dowodu pozostawiona
jest Czytelnikowi jako ćwiczenie. Niech teraz
h  0. Wówczas
u
0. Wówczas
u  x oraz
v
x oraz
v 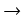 x, ponieważ u i v leżą pomiędzy x i x + h. Tym samym
x, ponieważ u i v leżą pomiędzy x i x + h. Tym samym
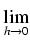 f
f (
u) =
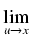 f
f (
u) =
f (
x)
oraz
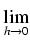 f
f (
v) =
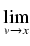 f
f (
v) =
f (
x),
ponieważ f jest ciągła w punkcie x. W połączeniu z wcześniejszymi rozważaniami i z twierdzeniem
o trzech ciągach daje to
g'(
x) =
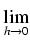
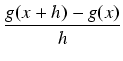
=
f (
x).
W poprzednim paragrafie obliczyliśmy kilka całek oznaczonych korzystając wprost z definicji - przekonaliśmy
się też, że na ogół bywa to dość uciążliwe. Udowodnimy teraz drugą część podstawowego twierdzenia
rachunku całkowego, zwaną też wzorem Newtona-Leibniza, która umożliwi nam stosunkowo łatwe obliczanie
całek oznaczonych.
Twierdzenie (wzór Newtona-Leibniza): Jeśli f jest funkcją ciągła na przedziale [a, b], to wówczas
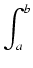 f
f (
x)
dx =
F(
b) -
F(
a),
gdzie F jest całką nieoznaczoną z funkcji f, a więc dowolną taką funkcją, że F' = f.
Dowód: Niech
g(x) = 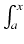 f (t)dt. Wiemy, że
g'(x) = f (x) - a zatem g jest całką nieoznaczoną
z funkcji f. Jeżeli F jest inną całką nieoznaczoną tej samej funkcji to, jak wiemy, różni się od g
co najwyżej o pewną stałą:
f (t)dt. Wiemy, że
g'(x) = f (x) - a zatem g jest całką nieoznaczoną
z funkcji f. Jeżeli F jest inną całką nieoznaczoną tej samej funkcji to, jak wiemy, różni się od g
co najwyżej o pewną stałą:
F(x) = g(x) + c
dla a < x < b. Wszelako zarówno F jak i g są ciągłe na przedziale [a, b], a więc rozważając
granice powyższych funkcji przy
x  a+ oraz
x
a+ oraz
x  b- widzimy, że powyższa
równośc zachodzi też dla x = a oraz x = b.
b- widzimy, że powyższa
równośc zachodzi też dla x = a oraz x = b.
Podstawiając x = a we wzorze na g(x) otrzymujemy
g(
a) =
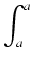 f
f (
t)
dt = 0,
co po połączeniu z wcześniejszymi rozważaniami daje
| F(b) - F(a) |
= |
(g(b) + C) - (g(a) + C) = |
|
| |
= |
g(b) - g(a) = g(b) = 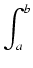 f (t)dt. f (t)dt. |
|
Przykład: Obliczyć całkę
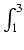 exdx.
exdx.
Funkcja
f (x) = ex jest ciągła w każdym punkcie przedziału [1, 3] i całka nieoznaczona z tej funkcji F
równa jest
F(x) + ex. Tak więc wobec wzoru Newtona - Leibniza:
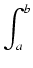 exdx
exdx =
F(3) -
F(1) =
e3 -
e.



Next: Podstawienia w całkach oznaczonych
Up: Rachunek całkowy
Previous: Całka oznaczona
Pawel Gladki
2006-01-30
![\includegraphics[width=12cm]{394-1.eps}](img720.gif)
![]() 0,
a więc
g(x) =
0,
a więc
g(x) = ![]() f (t)dt reprezentuje pole pod wykresem f od punktu a do punktu x. Aby obliczyć
pochodną funkcji g z definicji wpierw zauważmy, że dla h > 0 różnica
g(x + h) - g(x) jest różnicą pól figur,
a więc polem pod wykresem funkcji f od punktu x do x + h.
f (t)dt reprezentuje pole pod wykresem f od punktu a do punktu x. Aby obliczyć
pochodną funkcji g z definicji wpierw zauważmy, że dla h > 0 różnica
g(x + h) - g(x) jest różnicą pól figur,
a więc polem pod wykresem funkcji f od punktu x do x + h.
![\includegraphics[width=12cm]{395-5.eps}](img721.gif)
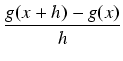
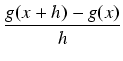 = f (x).
= f (x).
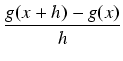 =
= ![\includegraphics[width=12cm]{396-6.eps}](img727.gif)
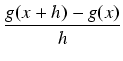
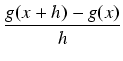 = f (x).
= f (x).
![]() f (t)dt. Wiemy, że
g'(x) = f (x) - a zatem g jest całką nieoznaczoną
z funkcji f. Jeżeli F jest inną całką nieoznaczoną tej samej funkcji to, jak wiemy, różni się od g
co najwyżej o pewną stałą:
f (t)dt. Wiemy, że
g'(x) = f (x) - a zatem g jest całką nieoznaczoną
z funkcji f. Jeżeli F jest inną całką nieoznaczoną tej samej funkcji to, jak wiemy, różni się od g
co najwyżej o pewną stałą:
![]() exdx.
exdx.