![\includegraphics[width=12cm]{369_1.eps}](img668.gif)
Rozważania dotyczące całek oznaczonych rozpoczniemy od próby rozwiązania następującego problemu: znaleźć pole obszaru S położonego pod krzywą y = f (x) między punktami a i b:
![\includegraphics[width=12cm]{369_1.eps}](img668.gif)
W pierwszej kolejności musimy sobie odpowiedzieć na pytanie, co rozumiemy pod pojęciem pola obszaru. Znamy odpowiedź w przypadku obliczania pól obszarów figur płaskich ograniczonych prostymi: znamy wzór na pole prostokąta, znamy wzór na pole trójkąta, możemy obliczyć też pole dowolnego wielokąta dzieląc go na trójkąty i sumując ich pola. Z doświadczenia wiemy jednak, że sprawa istotnie się komplikuje, gdy przychodzi nam policzyć pola figur "zaokrąglonych" - praktycznie jesteśmy bezradni w przypadku, gdy "zaokrąglenie" nie jest jakimś wycinkiem koła. Mamy oczywiście intuicyjne wyczucie, czym pole obszaru jest, a czym nie jest: spróbujemy teraz trochę tę intuicję sformalizować. Ogólnie rzecz biorąc, przybliżymy pole naszej figury za pomocą prostokątów, a następnie zdefiniujemy pole jako granicę sum pól prostokątów przy zwiększającej się ich liczbie. Zilustrujmy to na prostym przykładzie: chcemy policzyć pole pod parabolą y = x2 pomiędzy 0 i 1.
Oznaczmy figurę, której pola szukamy przez S i podzielmy ją na cztery paski S1, S2, S3 i S4 poprzez nakreślenie
pionowych linii
x = ![]() ,
x =
,
x = ![]() oraz
x =
oraz
x = ![]() (ilustracja (a) poniżej):
(ilustracja (a) poniżej):
![\includegraphics[width=12cm]{370_4.eps}](img669.gif)
Każdy z opisywanych prostokątów ma szerokość
![]() , zaś ich wysokości równe są, odpowiednio,
(
, zaś ich wysokości równe są, odpowiednio,
(![]() )2,
(
)2,
(![]() )2,
(
)2,
(![]() )2 i 12. Jeśli oznaczymy przez R4 sumę
pól naszych prostokątów, otrzymamy:
)2 i 12. Jeśli oznaczymy przez R4 sumę
pól naszych prostokątów, otrzymamy:
Zamiast przybliżać figurę S prostokątami takimi, jak na powyższej ilustracji, możemy użyć mniejszych prostokątów, których wysokości są wartościami funkcji f na lewych końcach przedziałów. Wówczas suma pól takich nowych prostokątów wyniesie:
Możemy teraz powtórzyć powyższą procedurę z większą liczbą pasków. Poniższa ilustracja pokazuje takie przybliżenie dla ośmiu pionowych pasków:
![\includegraphics[width=12cm]{371_6.eps}](img673.gif)
| n | Ln | Rn |
| 10 | 0,2850000 | 0,3850000 |
| 20 | 0,3087500 | 0,3587500 |
| 30 | 0,3168519 | 0,3501852 |
| 50 | 0,3234000 | 0,3434000 |
| 100 | 0,3283500 | 0,3383500 |
| 1000 | 0,3328335 | 0,3338335 |
Tabelka ta pozwala przypuszczać, że zarówno Ln jak i Rn przy kolejnych przybliżeniach zbliżają się
do
![]() . Faktycznie, sprawdzimy iż jest to prawdą w przypadku Rn. Ustalmy zatem liczbę n
prostokątów, z których każdy będzie miał szerokość
. Faktycznie, sprawdzimy iż jest to prawdą w przypadku Rn. Ustalmy zatem liczbę n
prostokątów, z których każdy będzie miał szerokość
![]() i wysokość będącą wartością funkcji
f (x) = x2
w punktach
i wysokość będącą wartością funkcji
f (x) = x2
w punktach
![]() ,
,
![]() ,
,
![]() , ...,
, ...,
![]() . Wobec tego wysokości równe
są, odpowiednio,
(
. Wobec tego wysokości równe
są, odpowiednio,
(![]() )2,
(
)2,
(![]() )2,
(
)2,
(![]() )2, ...,
(
)2, ...,
(![]() )2. Zatem:
)2. Zatem:
| Rn | = | ||
| = | |||
| = |
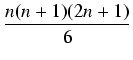 .
.
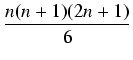 =
= 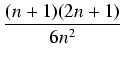 .
.
| = | 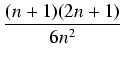 = = |
||
| = | 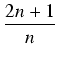 ) = ) = |
||
| = | |||
| = |
W podobny sposów możemy pokazać, że także dolna suma aproksymacyjna Ln dązy do
![]() , czyli:
, czyli:
Postaramy się teraz uogólnić poczynione obserwacje na przypadek dowolnej figury S leżącej pod wykresem funkcji y = f (x) między punktami a i b. Tak jak poprzednio, podzielmy figurę S na n pasków S1, S2,..., Sn równej szerokości:
![\includegraphics[width=12cm]{373_10.eps}](img686.gif)
Przybliżmy pole i -tego paska Si przez pole prostokąta o szerokości ![]() x i wysokości f (xi),
to jest wysokości równej wartości funkcji f w prawym końcu przedziału:
x i wysokości f (xi),
to jest wysokości równej wartości funkcji f w prawym końcu przedziału:
![\includegraphics[width=12cm]{373_11.eps}](img689.gif)
Definicja: Pole powierzchni A figury S położonej pod wykresem ciągłej funkcji f jest równe granicy sum aproksymujących prostokątów:
Można udowodnić, iż granica w powyższej definicji zawsze istnieje, o ile założymy, że funkcja f jest ciągła. Można również pokazać, że otrzymamy taką samą wartość A jeśli użyjemy lewych końców przedziałów przy konstrukcji aproksymujących prostokątów:
Zanim przejdziemy do podania formalnej definicji całki, rozwiążmy jeszcze jeden problem: znaleźć drogę, jaką przebył dany obiekt podczas pewnego przedziału czasu, jeśli prędkość danego obiektu była znana w każdej chwili danego przedziału czasowego. Jak dobrze wiemy, o ile tylko prędkość pozostaje stała, przebytą odległość potrafimy łatwo wyznaczyć ze wzoru:
| Czas (s) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| Prędkość (km/h) | 92 | 114 | 129 | 159 | 174 | 170 | 151 |
(autorzy FAQ nie zachęcają Czytelników do podróżowania z prędkościami odnotowanymi w tabeli). Aby czas i prędkość wyrażone zostały w zgodnych jednostkach, przekonwertujmy kilometry/godzinę na metry/sekundę przyjmując przelicznik 1 km/h = 0,27 m/s i zaokrąglając do całkowitych wyników:
| Czas (s) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| Prędkość (m/s) | 25 | 31 | 35 | 43 | 47 | 46 | 41 |
Podczas pierwszych pięciu sekund prędkość nie zmienia się znacząco, wobec tego możemy przybliżyć przebytą w tym czasie drogę zakładając, że prędkość była stała. Jeżeli więc założymy, że prędkość w ciągu pierwszych pięciu sekund była taka, jak na ich początku (tj. 25 m/s), to przebyta droga w przybliżeniu równa będzie:
Podobnie, podczas drugiego przedziału czasowego prędkość jest w przybliżeniu stała i wobec tego możemy przyjąć, że jest stale równa prędkości w chwili t = 5s. Tym samym możemy oszacować drogę przebytą między chwilami t = 5s a t = 10s w następujący sposób:
Jeżeli przeprowadzimy podobne rozumowanie dla każdego z występujących w tabeli interwału czasowego, to łączna przebyta droga będzie równa:
Zamiast rozważań prędkości mierzone na początkach każdego z przedziałów czasowych, możemy równie dobrze rozważać prędkości na końcach tych przedziałów. Otrzymalibyśmy wówczas:
Oczywiście chcąc otrzymać dokładniejszy wynik, musielibyśmy dokonywać pomiarów prędkości nie co 5 sekund, ale co 2 sekundy, lub - jeszcze lepiej - co sekundę. Rozważane sumy zaczynają nam zatem coś przypominać...
W ogólności, przypuśćmy że dany obiekt porusza się z prędkością zmienną w czasie i opisaną funkcją v = f (t),
gdzie
a ![]() t
t ![]() b oraz
f (t)
b oraz
f (t) ![]() 0 (ostatnie założenie oznacza, że obiekt porusza się stale w jednym
kierunku). Załóżmy, że dokonaliśmy pomiarów prędkości w chwilach
t0(= a), t1, t2,..., tn(= b)
w ten sposób, że prędkość obiektu jest mniej więcej stała na każdym przedziale czasowym wyznaczonym przez
dokonane pomiary. Jeżeli dodatkowo założymy, że wszystkie przedziały czasowe są jednakowej długości,
to czas upływający pomiędzy kolejnymi dwoma pomiarami wynosi
0 (ostatnie założenie oznacza, że obiekt porusza się stale w jednym
kierunku). Załóżmy, że dokonaliśmy pomiarów prędkości w chwilach
t0(= a), t1, t2,..., tn(= b)
w ten sposób, że prędkość obiektu jest mniej więcej stała na każdym przedziale czasowym wyznaczonym przez
dokonane pomiary. Jeżeli dodatkowo założymy, że wszystkie przedziały czasowe są jednakowej długości,
to czas upływający pomiędzy kolejnymi dwoma pomiarami wynosi
![]() t = (b - a)/n. W pierwszym przedziale
czasowym prędkość jest w przybliżeniu równa f (t0) i przebyta odległość wynosić będzie w przybliżeniu
f (t1)
t = (b - a)/n. W pierwszym przedziale
czasowym prędkość jest w przybliżeniu równa f (t0) i przebyta odległość wynosić będzie w przybliżeniu
f (t1)![]() t. Podobnie, w drugim przedziale czasowym przebyta droga wyniesie
f (t1)
t. Podobnie, w drugim przedziale czasowym przebyta droga wyniesie
f (t1)![]() i, konsekwentnie, całkowita droga przebyta w przedziale czasowym [a, b] wyniesie w przybliżeniu:
i, konsekwentnie, całkowita droga przebyta w przedziale czasowym [a, b] wyniesie w przybliżeniu:
Gdybyśmy zamiast lewych użyli prawych końców przedziałów czasowych, to przebyta droga byłaby w przybliżeniu równa:
Oczywiście im częściej dokonujemy pomiarów, tym dokładniejsze oszacowania drogi będziemy otrzymywać, a zatem wydaje się rozsądne aby przyjąć następującą definicję przebytej drogi:
Widzimy, że powyższe równanie jest dokładnie tej samej postaci, co wcześniej otrzymane równanie opisujące pole powierzchni figury ograniczonej wykresem funkcji - a zatem droga przebyta przez dany obiekt równa jest polu powierzchni pod wykresem funkcji prędkości zależnej od czasu. W dalszej części tego wykładu zobaczymy, że wiele innych wielkości występujących w przyrodzie można zinterpretować jako pole pod wykresem pewnej funkcji. Wobec tego powstaje konieczność zdefiniowania jednolitej teorii pozwalającej badać takie wielkości. W ten naturalny sposób wprowadzamy definicję całki oznaczonej:
Niech f będzie funkcją ciągła zdefiniowaną dla
a ![]() x
x ![]() b. Podzielmy przedział [a, b] na n
podprzedziałów o równej długości wynoszącej
b. Podzielmy przedział [a, b] na n
podprzedziałów o równej długości wynoszącej
![]() x = (b - a)/n. Niech
x0(= a), x1, x2,..., xn(= b)
będą końcami tych podprzedziałów i niech
x1*, x2*,..., xn* będą dowolnymi punktami próbkującymi
w tych przedziałach,
xi*
x = (b - a)/n. Niech
x0(= a), x1, x2,..., xn(= b)
będą końcami tych podprzedziałów i niech
x1*, x2*,..., xn* będą dowolnymi punktami próbkującymi
w tych przedziałach,
xi* ![]() [xi-1, xi]. Wówczas całkę oznaczoną z funkcji f w przedziale od
a do b oznaczamy i definiujemy jako:
[xi-1, xi]. Wówczas całkę oznaczoną z funkcji f w przedziale od
a do b oznaczamy i definiujemy jako:
Ponieważ założyliśmy, że f jest ciągła, można udowodnić, że granica podana w powyższej definicji zawsze istnieje i jest niezależna od wyboru punktów próbkujących. Bardziej precyzyjnie granicę tę możemy zapisać tak:
Symbol całki ![]() został wprowadzony przez Leibniza
i nawiązuje do kształtu literki S - jako, że mamy do czynienia z obliczaniem sum. W zapisie
został wprowadzony przez Leibniza
i nawiązuje do kształtu literki S - jako, że mamy do czynienia z obliczaniem sum. W zapisie
![]() f (x)dx
funkcję f nazywamy funkcją podcałkową, liczbę a dolną granicą całkowania, a liczbę b
górną granicą całkowania. Proces znajdowania całki zwiemy całkowaniem. Występującą w definicji
sumę
f (x)dx
funkcję f nazywamy funkcją podcałkową, liczbę a dolną granicą całkowania, a liczbę b
górną granicą całkowania. Proces znajdowania całki zwiemy całkowaniem. Występującą w definicji
sumę
![]() f (xi*)
f (xi*)![]() x nazywamy sumą Riemanna - w przypadku, gdy f przyjmuje wartości
dodatnie, może być interpretowana jako suma pól prostokątów, którymi przybliżamy pole pod wykresem funkcji.
x nazywamy sumą Riemanna - w przypadku, gdy f przyjmuje wartości
dodatnie, może być interpretowana jako suma pól prostokątów, którymi przybliżamy pole pod wykresem funkcji.
Podamy teraz kilka przykładów, w jaki sposób można obliczać całki oznaczone korzystając z definicji.
Przykład: Obliczyć całkę
![]() (x3 - 6x)dx.
(x3 - 6x)dx.
Dzielimy przedział [0, 3] na n podprzedziałów, każdy o długości
![]() x =
x = ![]() . Przedziały te
mają swe końce w punktach x0 = 0,
x1 =
. Przedziały te
mają swe końce w punktach x0 = 0,
x1 = ![]() ,
x2 =
,
x2 = ![]() i ogólnie
xi =
i ogólnie
xi = ![]() .
Jako że całka nie zależy od wyboru punktów próbkujących, możemy przyjąć, że znajdują się w prawych końcach
przedziałów. Wobec tego:
.
Jako że całka nie zależy od wyboru punktów próbkujących, możemy przyjąć, że znajdują się w prawych końcach
przedziałów. Wobec tego:
| = | |||
| = | |||
| = | |||
| = | |||
| = | 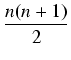 ]2 - ]2 - 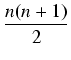 } = } = |
||
| = | |||
| = |
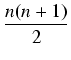 ,
,
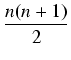 ]2.
]2.
W praktycznych zastosowaniach obliczanie całek jako granic sum Riemanna jest niezwykle uciążliwe i czasochłonne. W kolejnym paragrafie poznamy o wiele szybsze i sprawniejsze metody całkowania, ale zanim to zrobimy, zapoznamy się z kilkoma ogólnymi prawidłami rachunku całkowego.
Podczas definiowania całki
![]() f (x)dx milcząco założyliśmy, że a < b. Wszelako definicja całki
jako granicy sum Riemanna jest dobrze określona także wtedy, gdy a > b. Zauważmy, że jeśli zamienimy
miejscami a i b, to
f (x)dx milcząco założyliśmy, że a < b. Wszelako definicja całki
jako granicy sum Riemanna jest dobrze określona także wtedy, gdy a > b. Zauważmy, że jeśli zamienimy
miejscami a i b, to ![]() x zmieni się z
x zmieni się z
![]() na
na
![]() . Wobec tego:
. Wobec tego:
| = | |||
| = | |||
| = | |||
| = |
Powyższe własności pozostają prawdziwe niezależnie od tego, czy a < b, a = b czy też a > b. Obecnie podamy kilka
własności przy bardziej szczegółowych założeniach. Jeśli
f (x) ![]() 0 dla
a
0 dla
a ![]() x
x ![]() b, to wówczas
b, to wówczas