


Next: Całki funkcji trygonometrycznych
Up: Rachunek całkowy
Previous: Podstawowe własności całek. Całkowanie
Funkcją wymierną nazywamy iloraz dwóch wielomianów. Całka funkcji wymiernej jest więc postaci:
Każda całka z funkcji wymiernej jest kombinacją liniową następujących funkcji: funkcji wymiernej, logarytmu
funkcji liniowej, logarytmu funkcji kwadratowej o ujemnym wyróżniku i arcustangensa funkcji liniowej.
Przy obliczaniu całek z funkcji wymiernych postępujemy w następujący sposób:
- Jeżeli n
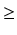 m, to licznik dzielimy przez mianownik i funkcję podcałkową przedstawiamy jako sumę
wielomianu oraz funkcji wymiernej, w której stopień licznika jest już mniejszy niż stopień mianownika (n < m).
Posługujemy się przy tym algorytmem pisemnego dzielenia wielomianów
m, to licznik dzielimy przez mianownik i funkcję podcałkową przedstawiamy jako sumę
wielomianu oraz funkcji wymiernej, w której stopień licznika jest już mniejszy niż stopień mianownika (n < m).
Posługujemy się przy tym algorytmem pisemnego dzielenia wielomianów
- Jeżeli n < m, to funkcję podcałkową rozkładamy na tzw. ułamki proste, tj. na wyrażenia postaci
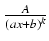
oraz
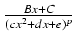
,
gdzie
A, B, C, a, b, c, d, e są stałe, przy czym
d2 -4ce < 0 (wyróżnik trójmianu
cx2 + dx + e jest ujemny),
zaś k i p są liczbami naturalnymi.
Sposób rozkładania funkcji wymiernej na ułamki proste oraz obliczania całek ułamków prostych zostanie
przedstawiony w przykładach
Przykład: Obliczyć całkę:

(
ax +
b)
ndx.
Jeżeli n jest liczbą ujemną, to zakładamy, że
ax + b 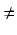 0. Jeżeli ponadto n nie jest liczbą
całkowitą, to zakładamy że
ax + b > 0. Wykonujemy podstawienie
ax + b = t, skąd adx = dt,
czyli
dx =
0. Jeżeli ponadto n nie jest liczbą
całkowitą, to zakładamy że
ax + b > 0. Wykonujemy podstawienie
ax + b = t, skąd adx = dt,
czyli
dx = 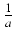 dt. Jeżeli n = - 1, to:
dt. Jeżeli n = - 1, to:

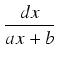
=
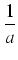

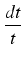
=
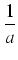
ln|
t| +
C =
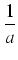
ln|
ax +
b| +
C.
Jeżeli n 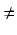 - 1, to:
- 1, to:

(
ax +
b)
ndx =
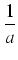
 tndt
tndt =
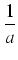 .
. 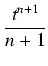
+
C =
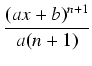
+
C.
Przykład: Obliczyć całkę:
Zakładamy, że
ax + b 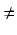 0. Zgodnie z uwagą ogólną, dzielimy licznik przez mianownik:
a więc
0. Zgodnie z uwagą ogólną, dzielimy licznik przez mianownik:
a więc

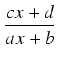 dx
dx =
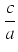
 dx
dx + (
d -
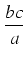
)

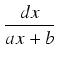
=
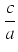 x
x +
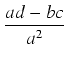
ln|
ax +
b| +
C.
Dalsze rozważania będą dotyczyły metod obliczania całek typu:
W pierwszej kolejności zawsze sprawdzamy, czy licznik nie jest pochodną mianownika (lub czy licznik nie jest
proporcjonalny do pochodnej mianownika). Wówczas wynik dostajemy natychmiast posługując się wzorem:
Przykład: Obliczyć całkę:

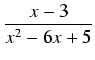 dx
dx.
Zauważmy, że
(x2 - 6x + 5)' = 2x - 6 = 2(x - 3), a więc pochodna mianownika jest proporcjonalna do licznika.
Zatem:

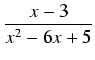 dx
dx =
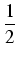

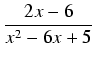 dx
dx =
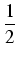
ln|
x2 - 6
x + 5| +
C.
Jeżeli licznik nie jest pochodną mianownika ani nie jest do niej proporcjonalny, to sposób obliczania
omawianych całek zależy od wyróżnika
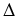 = b2 - 4ac trójmianu kwadratowego występującego w mianowniku
funkcji podcałkowej. Rozróżniamy trzy przypadki.
= b2 - 4ac trójmianu kwadratowego występującego w mianowniku
funkcji podcałkowej. Rozróżniamy trzy przypadki.
Przykład: Obliczyć całkę:

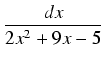
.
Wyróżnik trójmianu znajdującego się w mianowniku równy jest
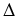 = 112 > 0, tak więc mianownik
ma dwa pierwiastki -5 i
= 112 > 0, tak więc mianownik
ma dwa pierwiastki -5 i
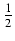 , a więc:
, a więc:
2
x2 +9
x - 5 = 2(
x -
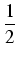
)(
x + 5) = (2
x - 1)(
x + 5).
1 = A(x + 5) + B(2x - 1) = (A + 2B)x + (5A - B).
Przyrównujemy współczynniki przy równych potęgach x po obu stronach i dostajemy:
A + 2B = 0 oraz
5A - B = 1.
Ten układ równań ma dokładnie jedno rozwiązanie, które znajdujemy jednym ze znanych sposobów dostając
A = 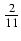 i
B = -
i
B = - 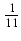 . Tym samym uzyskaliśmy następujący rozkład:
Całkujemy obie strony tożsamości i po prawej stronie wynosimy czynniki stałe przed całki:
. Tym samym uzyskaliśmy następujący rozkład:
Całkujemy obie strony tożsamości i po prawej stronie wynosimy czynniki stałe przed całki:
 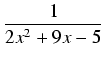 = =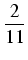  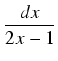 - -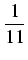  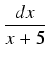 = = |
| |
= |
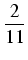 . . 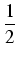 . ln| 2x - 1| - . ln| 2x - 1| - 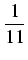 ln| x + 5| + C = ln| x + 5| + C = |
|
| |
= |
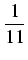 ln| 2x - 1| - ln| 2x - 1| - 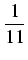 ln| x + 5| + C = ln| x + 5| + C = 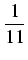 ln| ln|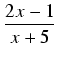 | + C. | + C. |
|
Przykład: Obliczyć całkę:

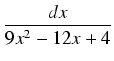
.
Wyróżnik trójmianu znajdującego się w mianowniku równy jest
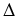 = 0, tak więc mianownik
jest kwadratem zupełnym:
= 0, tak więc mianownik
jest kwadratem zupełnym:
9x2 -12x + 4 = (3x - 2)2.
Na podstawie jednego z wcześniejszych przykładów obliczamy:
Przykład: Obliczyć całkę:

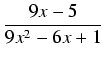 dx
dx.
Wyróżnik trójmianu znajdującego się w mianowniku równy jest
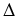 = 0, tak więc mianownik
jest kwadratem zupełnym:
= 0, tak więc mianownik
jest kwadratem zupełnym:
9x2 -6x + 1 = (3x - 1)2.
Rozkładamy funkcję podcałkową na sumę ułamków prostych:
Postępując podobnie jak w poprzednik przykładzie (a więc sprowadzając prawą stronę do wspólnego
mianownika, porównując liczniki, przyrównując w licznikach wyrażenia przy takich samych potęgach x'a
i rozwiązując odpowiedni układ równań) dostajemy:
Całkujemy obie strony tożsamości i po prawej stronie wynosimy czynniki stałe przed całki:
 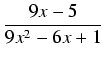 =-2 =-2 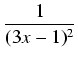 +3 +3 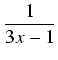 |
| |
= |
-2(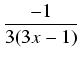 ) + 3 . ) + 3 . 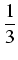 ln| 3x - 1| + C. ln| 3x - 1| + C. |
|
Przykład: Obliczyć całkę:

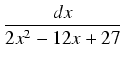
.
Wyróżnik trójmianu znajdującego się w mianowniku równy jest
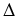 = - 72 = 0, tak więc mianownik
sprowadzamy do postaci kanonicznej trójmianu:
= - 72 = 0, tak więc mianownik
sprowadzamy do postaci kanonicznej trójmianu:
2
x2 -12
x + 27 = 2(
x -
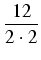
)
2 +
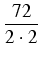
= 2(
x - 3)
2 + 9.
x - 3 =
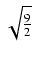
, skąd
dx =
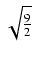 dt
dt.
Zatem:
W ten sposób zakończyliśmy badanie całek typu

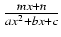 , rozpatrując wszystkie
możliwe przypadki w zależności od znaku wyróżnika mianownika. Przechodzimy teraz do obliczania całek
funkcji wymiernych, których mianowniki są wielomianami wyższego stopnia. Kluczowe znaczenie będzie dla
nas miała metoda rozkładania funkcji podcałkowej na ułamki proste - poznaliśmy ją już na kilku wybranych przykładach,
obecnie skupimy się na jej sformalizowaniu.
, rozpatrując wszystkie
możliwe przypadki w zależności od znaku wyróżnika mianownika. Przechodzimy teraz do obliczania całek
funkcji wymiernych, których mianowniki są wielomianami wyższego stopnia. Kluczowe znaczenie będzie dla
nas miała metoda rozkładania funkcji podcałkowej na ułamki proste - poznaliśmy ją już na kilku wybranych przykładach,
obecnie skupimy się na jej sformalizowaniu.
Rozważmy dowolną funkcję wymierną
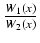 , dla której
deg W1(x) < deg W2(x).
Rozkładamy wielomian W2(x) na iloczyn wielomianów nierozkładalnych (jak wiadomo, będą to wielomiany
liniowe lub trójmiany kwadratowe o ujemnych wyróżnikach - lub ich potęgi). Postępujemy zgodnie z następującymi
trzema zasadami:
, dla której
deg W1(x) < deg W2(x).
Rozkładamy wielomian W2(x) na iloczyn wielomianów nierozkładalnych (jak wiadomo, będą to wielomiany
liniowe lub trójmiany kwadratowe o ujemnych wyróżnikach - lub ich potęgi). Postępujemy zgodnie z następującymi
trzema zasadami:
- Dla każdego czynnika postaci (ax + b)n w rozkładzie W2(x) do rozkładu na ułamki proste bierzemy
następujące składniki:
- Dla każdego czynnika postaci
(ax2 + bx + c)n, gdzie
ax2 + bx + c jest trójmianem o ujemnym
wyróżniku, do rozkładu na ułamki proste bierzemy następujące składniki:
- Suma ułamków prostych występująca w poszukiwanym rozkładzie jest sumą składników otrzymanych w
poprzednich dwóch punktach.
Przykład: Obliczyć całkę:

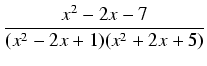 dx
dx.
Rozkładamy mianownik na czynniki nierozkładalne, otrzymując po nietrudnych rachunkach:
(x2 -2x + 1)(x2 +2x + 5) = (x - 1)2(x2 + 2x + 5).
Stosując powyższe uwagi o rozkładzie na ułamki proste, szukamy rozkładu w postaci:
Postępując podobnie jak w poprzednik przykładzie dostajemy:
Całkujemy:
Obliczenie pierwszych dwóch całek po prawej stronie nie nastręcza problemu, skupmy się więc na ostatniej całce:

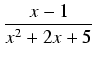 dx
dx.
Zastosujemy następującą sztuczkę: dzielimy licznik przez pochodną mianownika i otrzymujemy:
x - 1 =
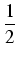
(2
x + 2) - 2,
skąd:
Obliczenie całek występujących po prawej stronie jest już proste - stosowne metody zostały omówione wcześniej.
Przykład: Obliczyć całkę:

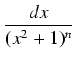
.
Oznaczmy przez
In = 
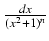 . Wyprowadzimy wzór rekurencyjny na In. Mamy oczywiście:
i wystarczy obliczyć drugą całkę występującą po prawej stronie równości. Mamy:
skąd całkujemy przez części przyjmując:
. Wyprowadzimy wzór rekurencyjny na In. Mamy oczywiście:
i wystarczy obliczyć drugą całkę występującą po prawej stronie równości. Mamy:
skąd całkujemy przez części przyjmując:
u(
x) =
x,
v'(
x) =
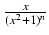
skąd
u'(
x) = 1,
v(
x) =

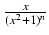 dx
dx = -
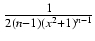
.
Otrzymujemy:
Podstawiając do wcześniejszej równości dostajemy
czyli
Przykład: Obliczyć całkę:

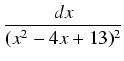
.
Stwierdzamy, że wyróżnik mianownika jest ujemny, całki tej nie potrafimy rozwiązać poznanymi dotąd metodami.
Zastosujemy następującą sztuczkę: sprowadzamy mianownik funkcji podcałkowej do postaci kanonicznej:
i wykonujemy podstawienie
x - 2 = 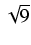 t, skąd dx = 3dt. Podstawiając mamy:
Ostatnią występująca w tym wzorze całkę obliczamy stosując wzór rekurencyjny z poprzedniego przykładu.
t, skąd dx = 3dt. Podstawiając mamy:
Ostatnią występująca w tym wzorze całkę obliczamy stosując wzór rekurencyjny z poprzedniego przykładu.
Czytelnik zweryfikuje, że stosując opisane w powyższych przykładach metody jesteśmy w stanie obliczyć
każdą całkę z funkcji wymiernej.
Ćwiczenia:
-

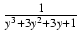 dy Odpowiedź:
-
dy Odpowiedź:
- 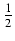 (y + 1)-2 + C
(y + 1)-2 + C
-

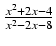 dx Odpowiedź:
x +
dx Odpowiedź:
x + 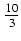 ln| x - 4| +
ln| x - 4| + 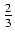 ln| x + 2| + C
ln| x + 2| + C
-

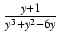 dy Odpowiedź:
-
dy Odpowiedź:
- 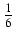 ln| y| -
ln| y| - 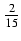 ln| y + 3| +
ln| y + 3| + 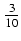 ln| y - 2| + C
ln| y - 2| + C
-

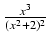 dx Odpowiedź:
dx Odpowiedź:
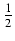 ln(x2 +2) +
ln(x2 +2) + 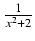 + C
+ C
-

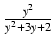 dy Odpowiedź:
y - 4 ln| y + 2| + ln| y + 1| + C
dy Odpowiedź:
y - 4 ln| y + 2| + ln| y + 1| + C
-

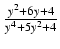 dy Odpowiedź:
ln(y2 +1) + arctg(y) - ln(y2 + 4) + C
dy Odpowiedź:
ln(y2 +1) + arctg(y) - ln(y2 + 4) + C
-

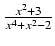 dx Odpowiedź:
-
dx Odpowiedź:
- 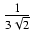 arctg(
arctg(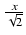 ) +
) + 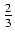 ln|
ln|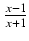 | + C
| + C
-

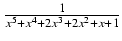 dx Odpowiedź:
dx Odpowiedź:
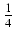 ln| x + 1| -
ln| x + 1| - 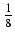 ln(x2 +1) +
ln(x2 +1) + 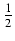 qrctg(x) +
qrctg(x) + 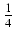 .
. 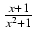 + C
+ C
-

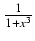 dx Odpowiedź:
dx Odpowiedź:
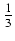 ln| x + 1| +
ln| x + 1| + 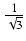 arctg(
arctg(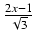 ) -
) - 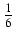 ln(x2 - x + 1) + C
ln(x2 - x + 1) + C
-

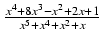 Odpowiedź:
ln| x| + ln(x2 - x + 1) - 2 ln| x + 1| -
Odpowiedź:
ln| x| + ln(x2 - x + 1) - 2 ln| x + 1| - 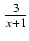 +
+ 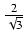 arctg(
arctg(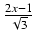 ) + C
) + C
Dodatkowe ćwiczenia



Next: Całki funkcji trygonometrycznych
Up: Rachunek całkowy
Previous: Podstawowe własności całek. Całkowanie
Pawel Gladki
2006-01-30
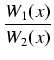 dx =
dx = 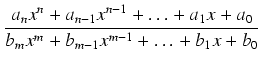 dx.
dx.
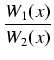 dx =
dx = 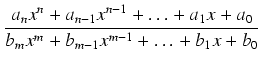 dx.
dx.
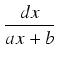 =
= 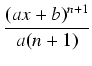 + C.
+ C.
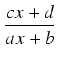 =
= 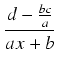 ,
,
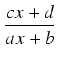 dx =
dx = 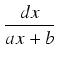 =
= 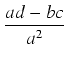 ln| ax + b| + C.
ln| ax + b| + C.
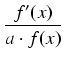 dx =
dx = 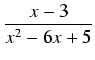 dx.
dx.
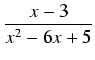 dx =
dx = 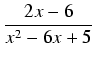 dx =
dx = ![]() = b2 - 4ac trójmianu kwadratowego występującego w mianowniku
funkcji podcałkowej. Rozróżniamy trzy przypadki.
= b2 - 4ac trójmianu kwadratowego występującego w mianowniku
funkcji podcałkowej. Rozróżniamy trzy przypadki.
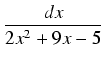 .
.
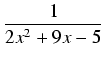 =
= 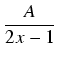 +
+ 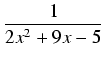 =
= 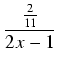 -
- 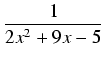 =
=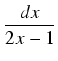 -
-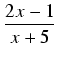 | + C.
| + C.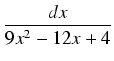 .
.
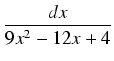 =
= 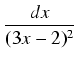 =
= 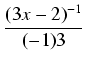 + C.
+ C.
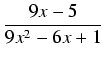 dx.
dx.
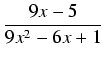 =
= 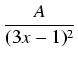 +
+ 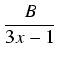 .
.
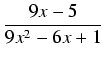 =
= 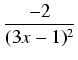 +
+ 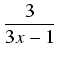 .
.
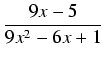 =-2
=-2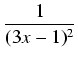 +3
+3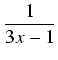
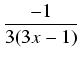 ) + 3 .
) + 3 . 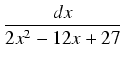 .
.
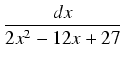 =
= 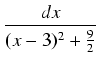 .
.
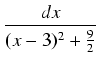 =
= 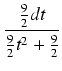 =
= ![]()
![]() , rozpatrując wszystkie
możliwe przypadki w zależności od znaku wyróżnika mianownika. Przechodzimy teraz do obliczania całek
funkcji wymiernych, których mianowniki są wielomianami wyższego stopnia. Kluczowe znaczenie będzie dla
nas miała metoda rozkładania funkcji podcałkowej na ułamki proste - poznaliśmy ją już na kilku wybranych przykładach,
obecnie skupimy się na jej sformalizowaniu.
, rozpatrując wszystkie
możliwe przypadki w zależności od znaku wyróżnika mianownika. Przechodzimy teraz do obliczania całek
funkcji wymiernych, których mianowniki są wielomianami wyższego stopnia. Kluczowe znaczenie będzie dla
nas miała metoda rozkładania funkcji podcałkowej na ułamki proste - poznaliśmy ją już na kilku wybranych przykładach,
obecnie skupimy się na jej sformalizowaniu.
![]() , dla której
deg W1(x) < deg W2(x).
Rozkładamy wielomian W2(x) na iloczyn wielomianów nierozkładalnych (jak wiadomo, będą to wielomiany
liniowe lub trójmiany kwadratowe o ujemnych wyróżnikach - lub ich potęgi). Postępujemy zgodnie z następującymi
trzema zasadami:
, dla której
deg W1(x) < deg W2(x).
Rozkładamy wielomian W2(x) na iloczyn wielomianów nierozkładalnych (jak wiadomo, będą to wielomiany
liniowe lub trójmiany kwadratowe o ujemnych wyróżnikach - lub ich potęgi). Postępujemy zgodnie z następującymi
trzema zasadami:
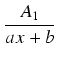 +
+ 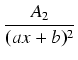 +...+
+...+ 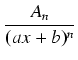 .
.
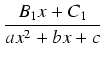 +
+ 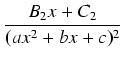 +...+
+...+ 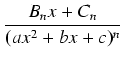 .
.
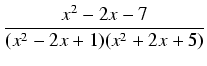 dx.
dx.
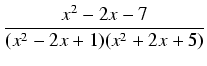 =
= 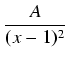 +
+ 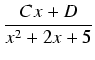 .
.
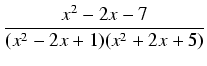 =
= 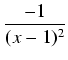 +
+ 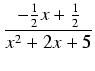 .
.
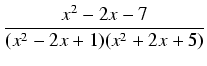 dx = -
dx = - 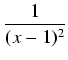 dx +
dx + 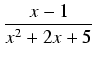 dx.
dx.
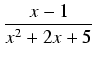 dx.
dx.
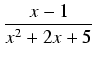 dx =
dx = 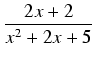 dx - 2
dx - 2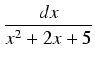 .
.
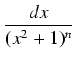 .
.
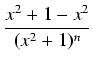 dx = In-1 -
dx = In-1 - 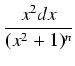
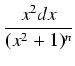 =
= 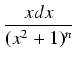 ,
,
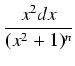 =
=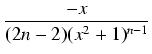 +
+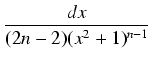 =
=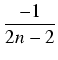 .
. 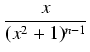 +
+ 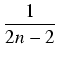 In-1
In-1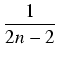 .
. 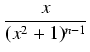 -
- 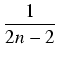 In-1
In-1
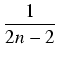 .
. 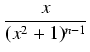 +
+ 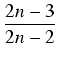 In-1.
In-1.
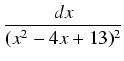 .
.
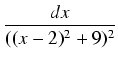
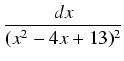 =
= 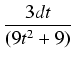 =
= 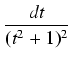 .
.