


Next: Niewymierność liczby
Up: Liczby rzeczywiste
Previous: Liczba e
Jak udowodnić, że pierwiastki z 2, 3, 5 lub, ogólniej, z dowolnej liczby pierwszej są liczbami niewymiernymi?
Niech p będzie liczbą pierwszą (tzn. jeśli p jest dzielnikiem iloczynu a . b, to p dzieli
co najmniej jeden z czynników - a lub b). Co by było, gdyby
x = 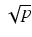 było liczbą wymierną?
Można by było zapisać x jako ułamek nieskracalny:
było liczbą wymierną?
Można by było zapisać x jako ułamek nieskracalny:
x =
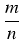
z naturalnymi n, m. Z określenia liczby x wynika, że x2 = p, czyli
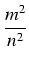
= 2
czyli
m2 = p . n2.
Jak widać, liczba m2 dzieli się przez p, ale jest iloczynem:
m2 = m . m, więc jeden
z czynników (m albo m albo oba na raz :-) ) musi się dzielić przez p. Niech
m = k . p.
Wstawiamy tę wartość do wyprowadzonej równości:
(pk)2 = pn2
skąd
(p2) . (k2) = pn2,
dzielimy obustronnie przez p:
p . k2 = n2
i okazuje się - na tej samej zasadzie, co w przypadku m - że n dzieli się przez p. To oznacza,
że i licznik, i mianownik nieskracalnego ułamka m/n dzielą się przez p - czyli ułamek jest
skracalny. Z zalożeń wywnioskowaliśmy zdanie sprzeczne z założeniami. Obliczenia są w porządku,
więc sprzeczność bierze się z założenia, że x można zapisać jako ułamek nieskracalny - czyli
z założenia, że x jest liczbą wymierną.
Ten dowód dla p = 2 przypisywany jest Pitagorasowi.



Next: Niewymierność liczby
Up: Liczby rzeczywiste
Previous: Liczba e
Pawel Gladki
2006-01-30
![]() było liczbą wymierną?
Można by było zapisać x jako ułamek nieskracalny:
było liczbą wymierną?
Można by było zapisać x jako ułamek nieskracalny: