


Next: Wielomiany i funkcje wymierne
Up: Liczby rzeczywiste
Previous: Niewymierność pierwiastków z liczb
Oczywiście to, że liczba 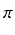 jest niewymierna wynika bezpośrednio z faktu, że jest to liczba przestępna.
Jednak podobnie jak w przypadku liczby e potrafimy podać krótki i elegancki dowód niewymierności.
jest niewymierna wynika bezpośrednio z faktu, że jest to liczba przestępna.
Jednak podobnie jak w przypadku liczby e potrafimy podać krótki i elegancki dowód niewymierności.
Zdefiniujmy funkcję:
Nietrudno sprawdzić, że
f(r)(0) = 0 dla r < n lub dla r > 2n. Dla
m 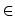 {1, 2,..., n - 1} mamy:
Wobec tego dla dowolnej liczby
s
{1, 2,..., n - 1} mamy:
Wobec tego dla dowolnej liczby
s 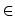
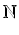 ,
f(s)(0) jest liczbą całkowitą; skoro
f (1 - x) = f (x),
również
f(s)(1) jest liczbą całkowitą. Jest jasne, że dla 0 < x < 1 mamy:
,
f(s)(0) jest liczbą całkowitą; skoro
f (1 - x) = f (x),
również
f(s)(1) jest liczbą całkowitą. Jest jasne, że dla 0 < x < 1 mamy:
0 <
f (
x) <
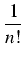
.
Zauważmy, iż wystarczy wykazać niewymierność liczby 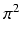 ; załóżmy więc dla dowodu nie wprost, że
; załóżmy więc dla dowodu nie wprost, że
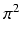 =
= 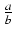 dla pewnych liczb całkowitych a i b. Dla dowolnej dodatniej liczby całkowitej
n zdefiniujmy
dla pewnych liczb całkowitych a i b. Dla dowolnej dodatniej liczby całkowitej
n zdefiniujmy
Fn(
x)
bn(
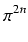 f
f (
x) -
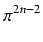 f''
f''(
x) +
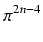 f(4)
f(4)(
x) -...+ (- 1)
nf(2n)(
x)).
Odnotujmy, iż Fn(0) oraz Fn(1) są liczbami całkowitymi. Prostym rachunkiem sprawdzamy, że:
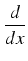 (F'n(x)sin (F'n(x)sin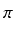 x- x-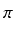 Fn(x)cos nx)=(Fn''(x)+ Fn(x)cos nx)=(Fn''(x)+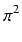 Fn(x))sin Fn(x))sin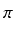 x= x= |
| |
= |
bn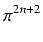 f (x)sin f (x)sin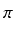 x = x = 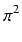 anf (x)sin anf (x)sin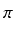 x x |
|
a więc
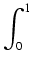
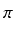 anf
anf (
x)sin
nxdx =
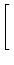
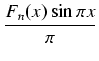
-
Fn(
x)cos
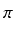 x
x![$\displaystyle \left.\vphantom{ \frac{F_n(x) \sin \pi x}{\pi} - F_n(x) \cos \pi x }\right]_{0}^{1}$](img274.gif)
=
Fn(1) +
Fn(0)
jest liczbą całkowitą. Ale ponieważ
0 < f (x) < 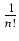 , otrzymujemy:
, otrzymujemy:
0 <
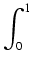
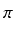 anf
anf (
x)sin
nxdx <
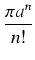
< 1



Next: Wielomiany i funkcje wymierne
Up: Liczby rzeczywiste
Previous: Niewymierność pierwiastków z liczb
Pawel Gladki
2006-01-30
![]() jest niewymierna wynika bezpośrednio z faktu, że jest to liczba przestępna.
Jednak podobnie jak w przypadku liczby e potrafimy podać krótki i elegancki dowód niewymierności.
jest niewymierna wynika bezpośrednio z faktu, że jest to liczba przestępna.
Jednak podobnie jak w przypadku liczby e potrafimy podać krótki i elegancki dowód niewymierności.
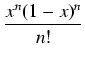 =
= 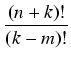 (- 1)kxk-m.
(- 1)kxk-m.
![]() ; załóżmy więc dla dowodu nie wprost, że
; załóżmy więc dla dowodu nie wprost, że
![]() =
= ![]() dla pewnych liczb całkowitych a i b. Dla dowolnej dodatniej liczby całkowitej
n zdefiniujmy
dla pewnych liczb całkowitych a i b. Dla dowolnej dodatniej liczby całkowitej
n zdefiniujmy
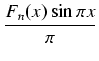 - Fn(x)cos
- Fn(x)cos