


Next: Jak obliczyć największy wspólny
Up: Liczby rzeczywiste
Previous: Jak zapisywać liczby w
Dla uproszczenia wypowiedzi przyjmujemy, że są tylko nieskończone ułamki dziesiętne:
0,5 = 0,50000... = 0,5(0). Skończony ułamek dziesiętny to taki nieskończony ułamek dziesiętny,
który od pewnego miejsca ma 0 w okresie.
Twierdzenie: Każda liczba wymierna jest wartością nieskończonego ułamka dziesiętnego okresowego.
Oczywiście okresowość zaczyna się od pewnego miejsca w rozwinieciu!
Dowód: Niech a będzie liczbą całkowitą, a b niech będzie liczbą całkowitą dodatnią.
Przypomnijmy, jak się zamienia ułamek zwykły a/b na ułamek dziesiętny:
- Dzielimy a z resztą przez b:
a =
a0 . b +
r1 i 0
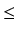 r1
r1 <
b
a więc:
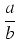
=
a0 +
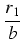
- Mnożymy pierwszą resztę przez 10 i iloczyn dzielimy z resztą przez b:
10
r1 =
a1 . b +
r2 i 0
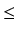 r2
r2 <
b
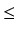 10r1/b < 10, czyli a1 daje pierwszą cyfrę
po przecinku rozwinięcia a/b na ułamek dziesiętny.
10r1/b < 10, czyli a1 daje pierwszą cyfrę
po przecinku rozwinięcia a/b na ułamek dziesiętny.
- Mnożymy drugą resztę przez 10 i iloczyn dzielimy z resztą przez b:
10
r2 =
a2 . b +
r3 i 0
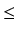 r3
r3 <
b
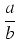
=
a0 +
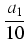
+
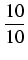 .
. 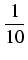 .
. 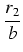
=
a0 +
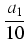
+
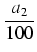
+
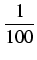 .
. 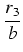
i a2 < 10 itd.
Poza kolejnymi cyframi dziesiętnymi an uzyskujemy jeszcze ciąg reszt rn, przy czym
dla każdego numeru n:
10
rn =
an+1 . b +
rn+1 i 0
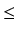 rn+1
rn+1 <
b.
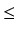 rn < b.
Oczywiście wyrazy tego ciągu nie mogą być wszystkie różne, bo jest tylko b liczb całkowitych
nieujemnych mniejszych od b. Ale jesli
rm = rm + s, to:
rn < b.
Oczywiście wyrazy tego ciągu nie mogą być wszystkie różne, bo jest tylko b liczb całkowitych
nieujemnych mniejszych od b. Ale jesli
rm = rm + s, to:
10rm = 10rm+s
zatem zachodzą równości:
am+1 = am+s+1 i rm+1 = rm+s+1.
W takim razie równe są też następne reszty i następne cyfry dziesiętne, itd. Na zasadzie
indukcji matematycznej ciągi cyfr i reszt od miejsca m są równe ciągom cyfr i reszt od miejsca
m + s. Zauważamy jeszcze, że
rm+2s = r(m+s)+s = rm+s = rm,
rm+3s = r(m+s)+2s = rm+2s = rm
itd., więc na zasadzie indukcji matematycznej
rm+ks = rm i
rm+ks+l = rm+l,
czyli ciąg reszt rn jest - od miejsca m - okresowy z okresem s. W takim razie również ciąg
an cyfr dziesiętnych jest od miejsca m okresowy z okresem s. Dowód jest zakończony.
Odwrotnie, wartością każdego ułamka dziesiętnego okresowego od miejsca m z okresem s jest liczba
wymierna:
| a0, a1a2...am-1(amam+1...am+s-1) |
= |
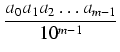 + + 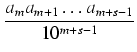 + + |
|
| |
+ |
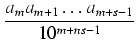 +... +... |
|
przesunięcie ciągu cyfr
amam+1...am+s-1 w prawo o s oznacza podzielenie przez
10s. To znaczy, że wartość tego ułamka dziesiętnego jest sumą tzw. przedokresu
p = a0a1a2...am-1/10m-1 i sumy wyrazów nieskończonego ciągu geometrycznego
o pierwszym wyrazie
w = amam+1...am+s-1/10m+s-1 i ilorazie q = 1/10s.
Interesująca nas wartość jest więc równa
p +
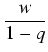
.
Liczby p, w, q są wymierne, więc i wartość jest liczbą wymierną.



Next: Jak obliczyć największy wspólny
Up: Liczby rzeczywiste
Previous: Jak zapisywać liczby w
Pawel Gladki
2006-01-30
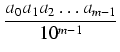 +
+ 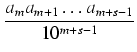 +
+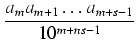 +...
+...