


Next: Jak wyznaczyć liczby całkowite
Up: Liczby rzeczywiste
Previous: Przedstawianie liczb wymiernych ułamkami
Sporo osób pamięta różne "metody" obliczania największego wspólnego dzielnika i chętnie raczy nimi
pytających, więc na początek podamy przykład, pozwalający łatwo ocenić praktyczną przydatność
różnych metod:
Obliczyć
NWD(2220 +1, 2223 + 1).
Nieznany jest ani jeden właściwy dzielnik żadnej z tych dwóch liczb (Fermata).
Praktycznym i szybkim sposobem obliczania największego wspólnego dzielnika dwóch liczb całkowitych
jest algorytm Euklidesa. Algorytm wykorzystuje nastepujące proste spostrzeżenie:
NWD(a, b) = NWD(b, a - kb).
Rzeczywiście, jeśli d jest wspólnym dzielnikiem liczb a i b, powiedzmy
a = da' i b = db' to
a - kb = da' - kdb' = d (a' - kb'), czyli d jest wspólnym dzielnikiem
liczb a i a - kb. Odwrotnie, jesli d jest wspólnym dzielnikiem liczb b i
c = a - kb,
to - na podstawie już udowodnionego - d jest wspólnym dzielnikiem liczb b i
c - (- k)b = a.
To oznacza, że pary liczb a, b oraz b, a - kb mają te same zbiory wspólnych dzielników,
a zatem i ten sam największy wspólny dzielnik. A teraz sam algorytm; ponieważ
NWD(a, b) = NWD(| a|,| b|),
oraz
NWD(a, 0) = a
więc wystarczy umieć obliczyć największy wspólny dzielnik dwóch liczb naturalnych. Pierwszy krok:
dzielimy a przez b z resztą:
a =
i1 . b +
r1 i 0
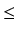 r1
r1 <
b;
otrzymujemy
r1 = a - i1 . b i NWD(a, b) = NWD(b, a - i1 . b) = NWD(b, r1).
Drugi krok: dzielimy b przez r1 z resztą:
b =
i2 . r1 +
r2 i 0
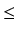 r2
r2 <
r1;
otrzymujemy
r2 = b - i2r1 i NWD(b, r1) = NWD(r1, b - i2 . r1) = NWD(r1, r2).
Trzeci krok: dzielimy r1 przez r2 z resztą, itd. - w każdym kroku dzielimy z resztą przedostatnią
resztę przez ostatnią.
Rezultatem jest malejący ciąg liczb
b > r1 > r2 >... i równości:
NWD(a, b) = NWD(rn, rn+1).
Ale nie może istnieć nieskończony malejący ciąg liczb naturalnych! Ciąg reszt musi się urwać,
czyli po pewnym rm nie ma już następnej reszty. Ale to, że nie można podzielić z resztą
liczby rm-1 przez rm oznacza, że rm = 0. Wobec tego
NWD(a, b) = NWD(rm-1, rm) = NWD(rm-1, 0) = rm-1.
Największym wspólnym dzielnikiem liczb a, b jest ostatnia niezerowa reszta rm-1 w algorytmie
Euklidesa. W naszym testowym przykładzie:
| 2223 + 1 |
= |
2223 -1 + 2 = 2222+1 - 1 + 2 = |
|
| |
= |
22 . 222 -1 + 2 = (2222)2 -12 + 2 = |
|
| |
= |
(2222 +1)(2222 - 1) + 2 = |
|
| |
= |
(2222 +1)(2221 +1)(2221 - 1) + 2 = |
|
| |
= |
(2222 +1)(2221 +1)(2220 -1)(2220 + 1) + 2 |
|
czyli pierwszą resztą jest 2. Dalej:
2220 +1 = 2220-1 . 2 + 1
więc drugą resztą jest 1, a trzecią resztą jest 0. Wobec tego
NWD(2220 +1, 2223 + 1) = 1.
Najwolniej algorytm Euklidesa działa dla pary kolejnych liczb Fibonacciego. Zatem liczba m
dzieleń w algorytmie Euklidesa nie przekracza
log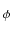 (b
(b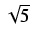 ) < 4 + log
) < 4 + log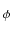 (b), gdzie
(b), gdzie
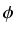 = (1 +
= (1 + 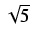 )/2,
)/2,
m < 4 + log
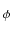
(
b) = 4 +
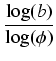
< 4 + 5 log(
b).



Next: Jak wyznaczyć liczby całkowite
Up: Liczby rzeczywiste
Previous: Przedstawianie liczb wymiernych ułamkami
Pawel Gladki
2006-01-30
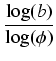 < 4 + 5 log(b).
< 4 + 5 log(b).