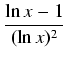W odróżnieniu od typowych zadań "na" procenty i układy równań z dwoma niewiadomymi, tu mamy ładne zadanie, którego treść mieści się w jednej linijce.
W zadaniach, w których coś się zmienia, warto przyjrzeć się temu, co się nie zmienia. W tym wypadku
zmieniają się podstawy i wykładniki. Sprowadzimy zagadnienie porównania wartości dwóch różnych funkcji
do porównania wartości jednej funkcji. Jakikolwiek ma być znak zamiast ![]() między porównywanymi
liczbami, kolejne nierówności są równoważne:
między porównywanymi
liczbami, kolejne nierówności są równoważne: