


Next: Co jest większe: e
Up: Śladami Lilavati
Previous: Paradoks więźnia, zazdrosny mąż
Mamy okrąg o promieniu r, na obwodzie okręgu wbity jest kołek, do którego przywiązana jest koza
na sznurku o długości R. Koza zjada trawę tak daleko jak pozwala jej sznurek R, zjadła tę trawę
w całym zasięgu sznurka R, tak że pole trawy zjedzonej równe jest polu trawy nie zjedzonej.
Jaki musi byc stosunek R/r, aby było to możliwe?
Przyjmijmy r = 1. Szukamy zatem R. Pole części wspólnej kół to:
P =
R . arccos(
R/2) + (
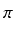
-2 arccos(
R/2)) +
R . 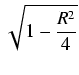
,
gdzie pierwszy składnik to pole wycinku koła o promieniu R, drugi składnik to pole wycinka
koła o promieniu 1, a trzeci to pole deltoidu będącego częścią wspólną wycinków. Ponieważ
P = 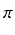 /2 (połowa pola całego koła o promieniu 1), zatem
/2 (połowa pola całego koła o promieniu 1), zatem
(
R2 -2)
. arccos(
R/2) +
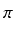
/2 -
R . 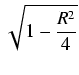
= 0.
R 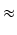
1.158728473018121517828233509933509149688292266492096511820695884820669802559196093199321610730860438
Zadanie o kozie ma tysiąc wcieleń. Zaczynało się od najprostszej postaci:
- Łąka ma kształt kwadratu o boku r. Właściciel uwiązał w rogu kozę na postronku długości r, a
kiedy koza zjadła całą dostępną zieleń, umocował postronek w sąsiednim rogu. Jaką część łąki objadła
koza?
- W założeniach poprzedniego zadania zmieniamy tylko długość postronka na R. Jakie musi być R,
żeby koza objadła połowę powierzchni łąki?
po bardzo nieprzyjemne rachunkowo:
- Koza uwiązana jest na postronku o długości R na łące na zewnątrz parkanu o planie okręgu
o promieniu r. Obliczyć powierzchnię, z której koza może zjeść trawę.
- Jw., tylko parkan jest eliptyczny, a koza przywiązana w jednym z wierzchołków elipsy.



Next: Co jest większe: e
Up: Śladami Lilavati
Previous: Paradoks więźnia, zazdrosny mąż
Pawel Gladki
2006-01-30
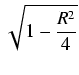 ,
,
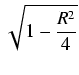 ,
,
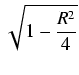 = 0.
= 0.