To, że nie znamy ogólnej metody rozwiązywania równań wielomianowych przez pierwiastniki nie oznacza, że
nie potrafimy podać innych metod ogólnych, przy pomocy których można wyrazić pierwiastki dowolnego wielomianu.
Około 1858 roku Hermite, Kronecker i Brioschi rozwiązali równanie stopnia piątego przy pomocy modularnych całek
eliptycznych. Nieco później, około roku 1870, Jordan udowadnia, że pierwiastki równania dowolnego
stopnia daje się wyrazić poprzez funkcje modularne, a siedem lat później Felix Klein wyraża pierwiastki
równania stopnia pięć przez funkcje hipergeometryczne. W latach 1884-1892 Lindemann podaje wzory
na pierwiastki dowolnego wielomianu z użyciem funkcji ![]() , a w 1915 roku Robert Hjalmal Mellin podaje
analogiczne wzory, tym razem z wykorzystaniem tzw. całek Mellina. W latach dwudziestych XX wieku podobne
rezultaty z użyciem funkcji hipergeometrycznych uzyskują Bierkeland, Capelli, Belardinelli, Pincherle,
Appell i Kampe de Feriet. Podamy - za książką D. Mumforda, "Tata Lectures on Theta", Birkhäuser, Boston
1983 (t. I), 1984 (t. II) - jeden z takich rezultatów, wykorzystujący funkcję
, a w 1915 roku Robert Hjalmal Mellin podaje
analogiczne wzory, tym razem z wykorzystaniem tzw. całek Mellina. W latach dwudziestych XX wieku podobne
rezultaty z użyciem funkcji hipergeometrycznych uzyskują Bierkeland, Capelli, Belardinelli, Pincherle,
Appell i Kampe de Feriet. Podamy - za książką D. Mumforda, "Tata Lectures on Theta", Birkhäuser, Boston
1983 (t. I), 1984 (t. II) - jeden z takich rezultatów, wykorzystujący funkcję ![]() .
.
Niech a0, a1,..., an będą liczbami zespolonymi, przy czym a0 jest różne od 0 i wielomian
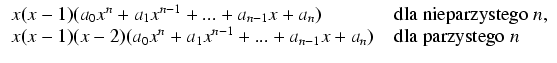
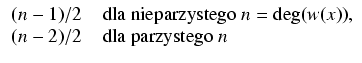
W następnej kolejności budujemy bazę grupy homologii
H1(C,![]() ) krzywej zespolonej C o równaniu
y2 = (x - x1) . ... . (x - x2g+1) w taki oto sposób: Odwzorowanie p(x, y) = x przekształca
krzywą C w dwulistne nakrycie prostej
) krzywej zespolonej C o równaniu
y2 = (x - x1) . ... . (x - x2g+1) w taki oto sposób: Odwzorowanie p(x, y) = x przekształca
krzywą C w dwulistne nakrycie prostej
![]() 1 (czyli płaszczyzny Gaussa), rozgałęzione w
punktach
x = x1, x = x2,..., x = x2g+1 i w nieskończoności. Z dokładnością do równoważności topologicznej
model krzywej C można zbudować, rozcinając
1 (czyli płaszczyzny Gaussa), rozgałęzione w
punktach
x = x1, x = x2,..., x = x2g+1 i w nieskończoności. Z dokładnością do równoważności topologicznej
model krzywej C można zbudować, rozcinając
![]() 1 wzdłuż łuków łączących x1 z x2,
x3 z x4, ..., x2g-1 z x2g, oraz x2g+1 z punktem w nieskończoności. Następnie dwa
egzemplarze takiej porozcinaniej płaszczyzny Gaussa sklejamy, łącząc ze sobą przeciwne brzegi każdego
rozcięcia - ale z różnych egzemplarzy płaszczyzny Gaussa. Bazę standardową tworzy 2g konturów
A1,..., Ag, B1,..., Bg takich, że:
1 wzdłuż łuków łączących x1 z x2,
x3 z x4, ..., x2g-1 z x2g, oraz x2g+1 z punktem w nieskończoności. Następnie dwa
egzemplarze takiej porozcinaniej płaszczyzny Gaussa sklejamy, łącząc ze sobą przeciwne brzegi każdego
rozcięcia - ale z różnych egzemplarzy płaszczyzny Gaussa. Bazę standardową tworzy 2g konturów
A1,..., Ag, B1,..., Bg takich, że:
Dla bazy standardowej A1,..., Ag, B1,..., Bg można utworzyć macierz okresów wybierając najpierw unormowaną bazę holomorficznych form różniczkowych
Niech zatem ![]() będzie macierzą okresów krzywej C względem standardowej bazy grupy
H1(C,
będzie macierzą okresów krzywej C względem standardowej bazy grupy
H1(C,![]() )
z numeracją zgodną z numeracją pierwiastków. Niech 2g + 1 będzie stopniem wielomianu w(x). Oznaczmy
)
z numeracją zgodną z numeracją pierwiastków. Niech 2g + 1 będzie stopniem wielomianu w(x). Oznaczmy
![]() -funkcja wielu zmiennych
-funkcja wielu zmiennych
![]() (z,
(z,![]() ) jest uogólnieniem klasycznej
) jest uogólnieniem klasycznej ![]() -funkcji,
funkcji analitycznej dwóch zmiennych
-funkcji,
funkcji analitycznej dwóch zmiennych
Ponadto oznaczmy:
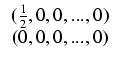
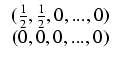
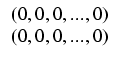
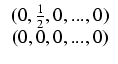
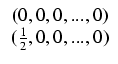
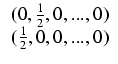
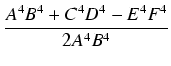 .
.