


Next: Wzory Newtona
Up: Rozwiązywanie równań
Previous: Zasadnicze twierdzenie algebry
Niech
f = f (X1, X2,..., Xn) będzie dowolnym wielomianem n zmiennych. Zmienne w tym wielomianie
możemy zamieniać kolejnością za pomocą permutacji 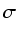 zbioru n-elementowego:
zbioru n-elementowego:
i otrzymać w ten sposób nowy wielomian
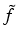 = f (X
= f (X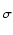 (1), X
(1), X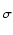 (2),..., X
(2),..., X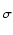 (n)).
Jeżeli tak otrzymany wielomian będzie identyczny z wyjściowym wielomianem, to wtedy wielomian f nazwiemy
wielomianem symetrycznym ze wzlgędu na permutację
(n)).
Jeżeli tak otrzymany wielomian będzie identyczny z wyjściowym wielomianem, to wtedy wielomian f nazwiemy
wielomianem symetrycznym ze wzlgędu na permutację 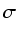 . Jeżeli wielomian jest symetryczny ze względu
na dowolna permutację jego zmiennych, to nazywamy go krótko wielomianem symetrycznym.
. Jeżeli wielomian jest symetryczny ze względu
na dowolna permutację jego zmiennych, to nazywamy go krótko wielomianem symetrycznym.
Przyjrzyjmy się kilku przykładom. Nietrudno się przekonać, że każdy z wielomianów:
X1 + X2 + X3, X12 + X22 + X32, X1X2 + X1X3 + X2X3
jest wielomianem symetrycznym. Faktycznie, chcąc zweryfikować symetryczność na przykład ostatniego z nich,
rozważamy sześć permutacji zbioru trzyelementowego, które dają nam następujące sześć wielomianów:
X1X2 + X1X3 + X2X3, X1X3 + X1X2 + X3X2, X2X1 + X2X3 + X1X3,
X2X3 + X2X1 + X3X1, X3X1 + X3X2 + X1X2, X3X2 + X3X1 + X2X1
i łatwo się przekonujemy, że każdy z nich równy jest wyjściowemu wielomianowi.
Rozważmy teraz wielomian n + 1 zmiennych f dany wzorem:
f (T, X1,..., Xn) = (T - X1)(T - X2)...(T - Xn).
Wymnóżmy wszystkie nawiasy po prawej stronie i uporządkujmy wyrazy według malejących potęg T:
| f (T, X1,..., Xn)=Tn-S1(X1,..., Xn)Tn-1+ |
| |
+ |
S2(X1,..., Xn)Tn-2 +...+ (- 1)nSn(X1,..., Xn). |
|
S1, S2,..., Sn są oczywiście wielomianami zmiennych
X1,..., Xn. Zauważmy, że są to wielomiany
symetrzyczne; w rzeczy samej, jakakolwiek permutacja zmiennych
X1,..., Xn nie zmienia wielomianu
f (T, X1,..., Xn), a więc w szczególności nie może zmienić współczynników stojących przy kolejnych
potęgach T. Prosty dowód indukcyjny pozwala sprawdzić, że wielomiany
S1,..., Sn wyrażają się wzorami:
S1 = X1 + X2 +...+ Xn
S2 = X1X2 + X1X3 +...+ X1Xn +...+ Xn-1Xn
S3 = X1X2X3 + X1X2X4 +...+ Xn-2Xn-1 + Xn
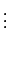
Sn = X1X2...Xn
Zatem wielomian
Sr(X1,..., Xn) jest sumą wszystkich możliwych jednomianów postaci:
Xk1Xk2...Xkr,
gdzie indeksy
k1,..., kr przyjmują wartości całkowite od 1 do n, z których żadne dwie nie są sobie równe.
Wielomiany te nazywamy wielomianami symetrycznymi podstawowymi.
Wielomian jednej zmiennej jest jednoznacznie wyznaczony (z dokładnością do stałej) przez swoje pierwiastki,
zatem możemy patrzeć na współczynniki wielomianu jako na wielomiany, których zmiennymi są pierwiastki.
Okazuje się, że można je łatwo wyznaczyc w terminach wielomianów symetrycznych podstawowych. Dokładniej,
jeżeli
c1,..., cn sa pierwiastkami wielomianu:
g(t) = a0tn + a1tn-1 +...+ an-1t + an
to wówczas:
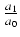 = - S1(c1, c2,..., cn)
= - S1(c1, c2,..., cn)
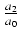 = S2(c1, c2,..., cn)
= S2(c1, c2,..., cn)
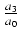 = - S3(c1, c2,..., cn)
= - S3(c1, c2,..., cn)
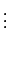
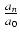 = (- 1)nSn(c1, c2,..., cn).
= (- 1)nSn(c1, c2,..., cn).
Faktycznie, zauważmy że:
g(t) = a0(t - c1)...(t - cn)
i zastosujmy do powyższego wielomianu wyprowadzone wcześniej wzory.
W szczególności wzory te dla wielomianu stopnia dwa:
g(t) = a0t2 + a1t + a2
zapiszą się jako:
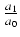 = - c1 - c2
= - c1 - c2
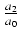 = c1c2,
= c1c2,
dla wielomianu stopnia trzy:
g(t) = a0t3 + a1t2 + a2t + a3
jako:
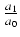 = - c1 - c2 - c3
= - c1 - c2 - c3
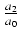 = c1c2 + c1c3 + c2c3
= c1c2 + c1c3 + c2c3
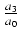 = - c1c2c3
itd.
= - c1c2c3
itd.



Next: Wzory Newtona
Up: Rozwiązywanie równań
Previous: Zasadnicze twierdzenie algebry
Pawel Gladki
2006-01-30
![]() zbioru n-elementowego:
zbioru n-elementowego: