Zasadnicze twierdzenie algebry

Zasadnicze twierdzenie algebry orzeka, że ciało liczb zespolonych jest algebraicznie domknięte - innymi słowy, że każdy wielomian o współczynnikach zespolonych ma w ciele liczb zespolonych pierwiastek. Po raz pierwszy zostało ono sformułowane przez Girarda w 1629 roku, a pełny dowód jako pierwszy podał Gauss w 1799. Zasadnicze twierdzenie algebry jest "zasadnicze" tylko z historycznego punktu widzenia i obecnie przyjęta nazwa wydaje się dziś nieco przesadzona, pochodzi jednak z czasów, gdy problem rozwiązalności równań algebraicznych był jednym z głównych tematów zainteresowań matematyków. Przeciętny student matematyki poznaje w toku swych studiów przynajmniej dwa dowody tego twierdzenia: na wykładzie z analizy zespolonej, gdzie twierdzenie to jest prostym wnioskiem z twierdzenia Liouville'a i na wykładzie z algebry, gdzie dowód ilustruje "jak działa" grupa Galois rozszerzenia $\mathbb {R}$ $\subset$ $\mathbb {C}$. Istnieje całe mnóstwo dowodów zasadniczego twierdzenia - my podamy jeden z nich, korzystający z twierdzenia Weierstrassa, które jest ważnym, ale stosunkowo prostym faktem z analizy matematycznej, znanym w zasadzie licealistom (no, może nie wszystkim... :) ).

Twierdzenie Weierstrassa: Funkcja ciągła na zbiorze zwartym o wartościach rzeczywistych przyjmuje wartości największą i najmniejszą.

Dowód zasadniczego twierdzenia algebry opiera się teraz na dwóch lematach:

Lemat 1: Niech P(Z) = a_nZⁿ +...+ a₁Z + a₀ $\in$ $\mathbb {C}$[Z], | a_n = 1|, niech p : $\mathbb {C}$ $\rightarrow$ $\mathbb {R}$ będzie dana wzorem p(z) = | P(z)|. Wówczas p osiąga kres dolny na zbiorze $\mathbb {C}$.

Dowód: Wobec nierówności trójkąta dla modułu:

$${\frac{{a_{n-1}}}{{z}}} {\frac{{a_0}}{{z}}}$$ p(z) =

$$\geq {\frac{{\vert a_{n-1}\vert}}{{\vert z\vert}}} {\frac{{\vert a_0\vert}}{{\vert z\vert^n}}} \geq {\frac{{n \cdot \max \{\vert a_i\vert: i \in \{0, \ldots, n-1\} \}}}{{R}}}$$

dla | z| $\geq$ R $\geq$ 1. Niech R = 2(1 + max{| a_i| : i $\in$ {0,..., n - 1}}). Wówczas p(z) $\geq$ ${\frac{{1}}{{2}}}$Rⁿ > | a₀| = p(0) dla | z| $\geq$ R. Zatem wewnątrz koła {z : | z| $\leq$ R} istnieje punkt, w którym wartość p jest mniejsza od wartości w dowolnym punkcie poza kołem {z : | z| $\leq$ R}. Wobec tego inf{p(z) : z $\in$ $\mathbb {C}$} = inf{p(z) : | z| $\leq$ R}. Ponieważ koło {z $\in$ $\mathbb {C}$ : | z| $\leq$ 1} jest zbiorem zwartym, więc wobec twierdzenia Weierstrassa funckcja p osiąga na nim kres dolny.

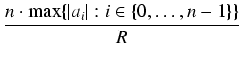Lemat 2: Niech P(Z) = a_nZⁿ +...+ a₁Z + a₀ $\in$ $\mathbb {C}$[Z], | a_n = 1|, niech p : $\mathbb {C}$ $\rightarrow$ $\mathbb {R}$ będzie dana wzorem p(z) = | P(z)|. Niech ponadto p(z₀) = inf{p(z) : z $\in$ $\mathbb {C}$}. Wówczas P(z₀) = 0.

Dowód: Przypuśćmy, że P(z₀)
neq0, P(z₀) = m, m $\in$ $\mathbb {R}$₊. Niech $\rho$ $\in$ (0, min{1, m}). Niech z $\in$ $\partial$K(z₀,$\rho$) (w ten sposób oznaczamy brzeg koła o środku z₀ i promieniu $\rho$). Wówczas z = z₀ + $\rho$e^i$\theta$. Mamy:

P(z₀ + $$\rho$$e^i$\theta$) = $$\sum_{{k=0}}^{n}$$a_k(z₀ + $$\rho$$e^i$\theta$)^k = P(z₀) + w₁(z₀)$$\rho$$e^i$\theta$ +...+ w_n(z₀)$$\rho^{n}_{}$$e^in$\theta$,

gdzie w₁(z₀),..., w_n(z₀) są pewnymi współczynnikami.

Pokażemy, że dla pewnej liczby j $\in$ {1,..., n}, w_j(z₀) $\neq$ 0. Istotnie, przypuśćmy że w₁(z₀) =...= w_n(z₀) = 0. Wówczas P jest stały na $\partial$K(z₀,$\rho$), a więc wielomian Q(Z) = P(Z) - P(z₀) stopnia dodatniego ma nieskończenie wiele pierwiastków, co jest sprzecznością.

Niech zatem k = min{j $\in$ {1,..., n} : w_j(z₀) $\neq$ 0}. Mamy więc:

| P(z₀ + $$\rho$$e^i$\theta$)| $$\leq$$ | P(z₀) + w_k(z₀)$$\rho^{k}_{}$$e^ik$\theta$| + (1 + n ^. max{| w_j(z₀)| : j $$\in$$ {1,..., n}})$$\rho^{{k+1}}_{}$$.

Połóżmy $\theta$ = ${\frac{{\pi - Arg(w_k(z_0))}}{{k}}}$. Wówczas:

| P(z₀ + $$\rho$$e^{i${\frac{{\pi - Arg(w_k(z_0))}}{{k}}}$})| $$\leq$$ | P(z₀)| - | w_k(z₀)|$$\rho^{k}_{}$$ + (1 + n ^. max{| w_j(z₀)| : j $$\in$$ {1,..., n}})$$\rho^{{k+1}}_{}$$.

Niech teraz $\rho$ < ${\frac{{\vert w_k(z_0)\vert}}{{1 + n \cdot \max \{\vert w_j(z_0)\vert: j \in \{1, \ldots, n\}\}}}}$. Wówczas:

| P(z₀)| - | w_k(z₀)|$$\rho^{k}_{}$$ + (1 + n ^. max{| w_j(z₀)| : j $$\in$$ {1,..., n}})$$\rho^{{k+1}}_{}$$ < | P(z₀)| = P(z₀) = m = inf{p(z) : z $$\in$$ $$\mathbb {C}$$},

więc p(z₀ + $\rho$e^{i${\frac{{\pi - Arg(w_k(z_0))}}{{k}}}$}) < inf{p(z) : z $\in$ $\mathbb {C}$} - sprzeczność.

Oczywiście z Lematu 2 wynika natychmiast zasadnicze twierdzenie algebry.