


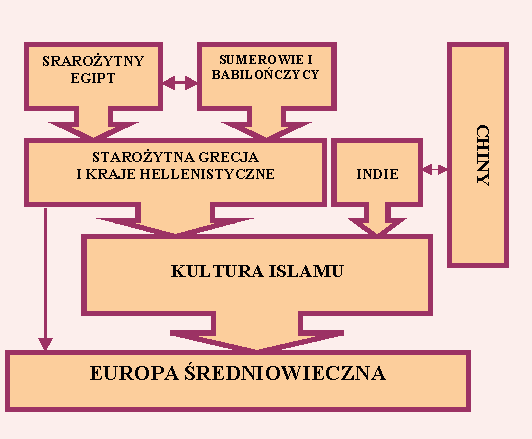
Nasza wędrówka z liczbą przez wieki ma już kilka tysięcy lat. Wzajemne powiązania pomiędzy różnymi obszarami kulturowymi można sobie wyobrazić mniej więcej tak:
|
Jak widać, duże znaczenie dla postępu wiedzy matematycznej w Europie miały dzieła matematyków arabskich. To dzięki Arabom upowszechniły się w Europie:
Wsród Europejczyków - matematyków, na uwagę zasługują:

Mnichowi Gerbertowi Europa Średniowieczna zawdzięcza upowszechnienie ABAKU, czyli
liczydła (skonstruowanego z deski podzielonej na 30 kolumn).

Fibonacci jest autorem "Księgi abaku", przy czym abak jst tu rozumiany nie jako urządzenie do liczenia, ale jako arytmetyka w ogóle. To własnie w tym dziele pisze Fibonacci o cyfrach arabskich i o systemie dziesiętnym (z wiedzą na ten temat zapoznał się podczas podróży po krajach muzułmańskich północnej Afryki). Autor zachęca Europejczyków do stosowania dziesiętnego systemu pozycyjnego, przytaczając tablicę porównawczą z zapisem liczb cyframi rzymskimi i arabskimi. Na przykład:
W "Księdze Abaku" pojawiają się, po raz pierwszy w Europie, liczby ujemne.
U Fibonacciego spotykamy wiele zadań arytmetycznych, w tym zadanie o kotach, z którym mieliśmy okazję się już spotkać, czytając o matematyce egipskiej. Ale Fibonacci zasłynął bardziej innym zadaniem "zoologicznym". Jest to zadanie o mnożących sie przez rok królikach. (Ile potomstwa i potomstwa potomstwa, itd., potrafi wydać jedna para w ciągu roku.) O tym zagadnieniu możesz przeczytać w zadaniu zamieszczonej na końcu strony!



Jesteśmy coraz bliżej naszych czasów. Wiedza matematyczna (i nie tylko matematyczna - oczywiście) zaczyna sie rozrastać. Pojawia się wielu uczonych, a każdy z nich ma na swym koncie wiele badań, z których do dziś korzystamy. Więc wypunktujmy tylko fakty, ważne z punktu widzenia rozwoju pojęcia liczby:

Zapamiętaj
 Ciekawostka
Ciekawostka