

Dla Pitagorejczyków liczba, to liczba całkowita dodatnia. Rozumieli ją jako zbiór jedności.( Podstawą wszechrzeczy jest jedność czyli monada - matka wszystkich liczb.) Liczby uważali za niepodzielne i wyobrażali je sobie jako punkty, które rozmieszczali w postaci foremnych figur geometrycznych. Otrzymywali w ten sposób liczby: trójkątne, czworokątne, pięciokątne, itd.
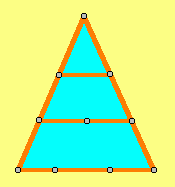
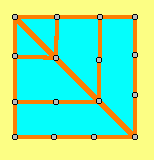
| Liczby trójkątne | Liczby czworokątne | Liczby pięciokątne |
|---|---|---|
 |
 |
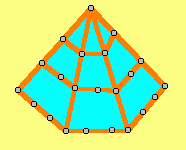 |
| 3=1+2 | 4=1+3 | 5=1+4 |
| 6=1+2+3 | 9=1+3+5 | 12=1+4+7 |
| 10=1+2+3+4 | 16=1+3+5+7 | 22=1+4+7+10 |
Pitagorejczycy dzielili liczby na parzyste i
nieparzyste; dokonywali równeż podziału na liczby
pierwsze i liczby złożone.
Badając własności liczb złożonych, pierwsi zwrócili uwagę na prawa podzielności.
Znali przykłady liczb, które nazywamy doskonałymi.
| Liczbę nazywamy doskonałą, jeśli jest równa sumie wszystkich swoich dzielników, mniejszych od niej samej. |
|---|
Doskonałe są np:
Zajmowali się liczbami o pięknej nazwie: zaprzyjaźnione.
|
Liczby n i m są zaprzyjaźnione, jeżli równocześnie: suma wszystkich dzielników n (mniejszych od niej samej) jest równa liczbie m, suma wszystkich dzielników m (mniejszych od niej samej) jest równa liczbie n. |
|---|
Parą liczb zaprzyjaźnionych jest np: (220, 284).
Warto jeszcze powiedzieć, co rozumiemy przez trójki pitagorejskie.
Są to liczby spełniające równanie:
Najmniejsza trójka pitagorejska, to (3, 4, 5).
Czy Pitagorejczycy znali liczby wymierne?
Posługiwali się takimi wielkościami, ale nie nazywali ich liczbami. Były to dla nich
stosunki liczb całkowitych.
Problem niewymierności.
Jest to zagadnienie, wokół którego narosło wiele mitów. O szczególnej liczbie niewymiernej - złotej liczbie, która
fascynowała starożytnych Greków możesz przeczytać w ciekawostkach zamieszczonych
na końcu tej strony!
Pitagorejczycy, jak się zdążyliśmy
przekonać, łączyli ściśle teorię liczb z geometrią. Wspomniane "stosunki liczb" były stosunkami
długości odcinków. Początkowo Pitagorejczycy sądzili, że wszystkie odcinki są
współmierne. Później jednak zaczęli dochodzić do wniosku, że tak nie jest.
Do odkrycia tego mogło doprowadzić badanie kwadratu i jego przekątnej (są niewspółmierne);
być może było efektem zajmowania się średnią geometryczną.
Niektóre źródła podają, że niewymierność odkrył wywodzący się ze Szkoły Pitagorejskiej
Hippasus, dowodząc, że przekątna pięciokąta foremnego jest niewspółmierna z jego bokiem.
Faktem jest, że to ważne odkrycie było niedoceniane przez samych Pitagorejczyków, a wręcz było ukrywane, jako że stało w sprzeczności z wyznawaną ideologią.
Symbolika liczb według Pitagorejczyków.
Ponieważ, według filozofii Pitagorejczyków, początkiem wszechrzeczy jest liczba, więc wszystko
co nas otacza jest symbolizowane przez liczby, bądź (wywodzące się oczywiście od liczb) -
figury geometryczne:
Wielościany są symbolami żywiołów i tego, co nas otacza:
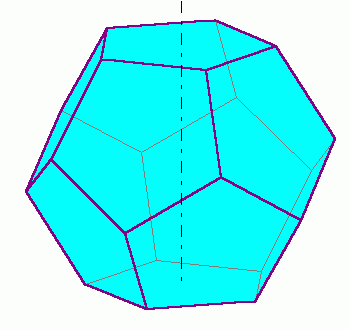
Symbolem wszechświata jest dwunastościan foremny.
Zapamiętaj
| Anegdota Ciekawostka |
 |
Zadanie |