Obszaru tego nie możemy rozłożyć na kwadraty
lub trójkąty, nie podamy zatem
wzoru na pole S w postaci sumy skończonej.
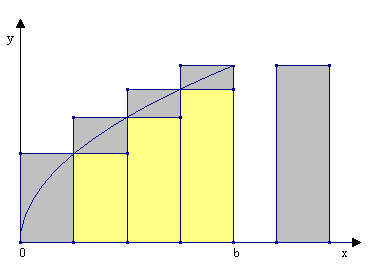
Możemy natomiast znaleźć przybliżoną wartość S.
Pojęcie całki oznaczonej.
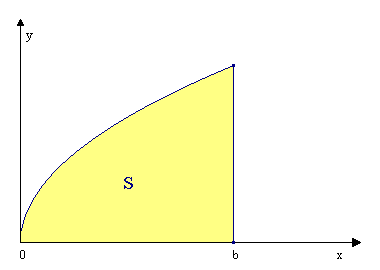
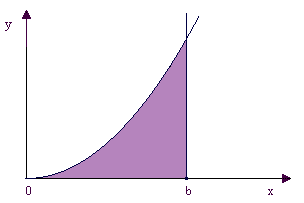
Już w III wieku p.n.e. zastanawiano się nad sposobem wyznaczenia pola figury, która nie jest ograniczona wielokątami

|
Niech S oznacza jego pole. Obszaru tego nie możemy rozłożyć na kwadraty lub trójkąty, nie podamy zatem wzoru na pole S w postaci sumy skończonej. Możemy natomiast znaleźć przybliżoną wartość S. |
|

|
|
|
wykorzystaj przyciski.  |

 .
.
|

|
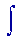 , wymyślił i wprowadził G.W.Leibniz. Podkreśla on sposób otrzymywania całki jako granicy ciągu pewnych sum.
, wymyślił i wprowadził G.W.Leibniz. Podkreśla on sposób otrzymywania całki jako granicy ciągu pewnych sum.
|

|
|
|
|
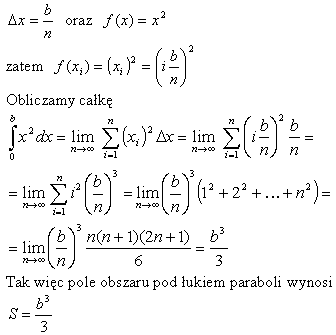
|
|
Obliczanie całki oznaczonej z definicji jest kłopotliwe. Jeśli chcesz przekonać się czy istnieje prostsza metoda, przejdź do następnej strony. |

|