Pojęcia Podstawowe   O Autorze
Sposoby Opisu Test Linki
Funkcja Liniowa   Wyślij List

FUNKCJA LINIOWA

Funkcję określoną wzorem  y=ax+b

gdzie a, b-ustalone liczby rzeczywiste, x należy do R

nazywamy funkcją liniową.



I przykład

Z podanych funkcji wybierz funkcje liniowe, wpisując literę L w odpowiednią kratkę (jeśli dana funkcja nie jest liniowa, wpisz N).
y = 2x
y = -4x + 2
y = -5
y = x3
y = 1 – 0,2x
y = x2 + 1




II przykład


Funkcja liniowa jest rosnąca, gdy .

Funkcja liniowa jest malejąca, gdy .

Funkcja liniowa jest stała, gdy .




III Przykład

Sporządź wykres funkcji y=0,5x+2, której dziedziną jest:

a) Zbiór liczb rzeczywistych.

b) Zbiór liczb całkowitych.

c) Zbiór liczb rzeczywistych z przedziału <-2; 4>

 





IV przykład

.  y=2x-4;  x należy do zbioru R
Odczytaj własności funkcji z wykresu:


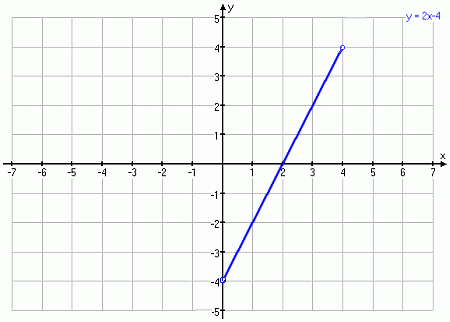
1 . D=(;)

2 .Miejsce zerowe funkcji wynosi

3 . Funkcja jest rosnąca dla x należącego do przedziału (;)

4 . Funkcja przyjmuje wartości dodatnie dla x należącego do przedziału (;)

5 . Funkcja przyjmuje wartości ujemne dla x należącego do przedziału (;)




V przykład
y=x
y=x+2
y=x-3                   

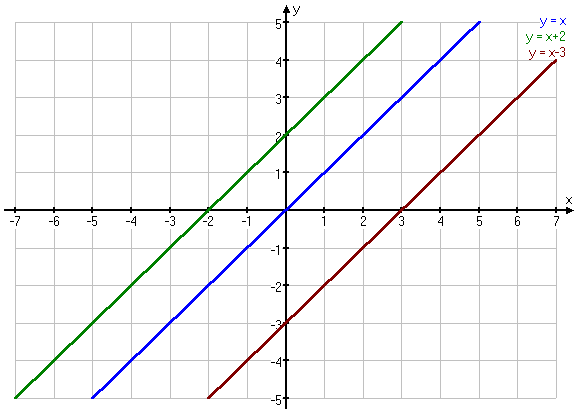
Wykresy tych funkcji są równoległe, gdyż współczynniki kierunkowe a są .