Momenty i środki mas

Naszym głównym celem w tym paragrafie będzie wyznaczenie punktu P na płycie o zadanym kształcie w ten sposób, aby płyta podparta w tym punkcie utrzymywała się w pozycji poziomej.

Rozważmy najpierw prostszą sytuację, w której dwa obiekty o masach m₁ i m₂ połączone są sztywnym drutem o pomijalnej masie, który podparty jest w położeniu równowagi w odległości d₁ od masy m₁ i d₂ od masy m₂. Nasz układ pozostanie w stanie równowagi, jeśli spełniona będzie następująca równość:

m₁d₁ = m₂d₂.

Przyjmijmy dla wygody obliczeń, że drut leży na osi x z masą m₁ w punkcie o współrzędnej x₁ i z masą m₂ w punkcie o współrzędnej x₂. Niech $\overline{{x}}$ oznacza współrzędną punktu równowagi. Otrzymujemy wobec tego d₁ = $\overline{{x}}$ - x₁ oraz d₂ = $\overline{{x}}$ - x₂

Tym samym powyższe równanie przepisze się jako

m₁($$\overline{{x}}$$ - x₁) = m₂(x₂ - $$\overline{{x}}$$)

m₁$$\overline{{x}}$$ + m₂$$\overline{{x}}$$ = m₁x₁ + m₂x₂

$$\overline{{x}}$$ = $${\frac{{m_1 x_1 + m_2 x_2}}{{m_1 + m_2}}}$$

Liczby m₁x₁ oraz m₂x₂ nazywamy momentami mas m₁ i m₂, odpowiednio. Równanie powyższe orzeka więc, że centrum masy $\overline{{x}}$ znajdujemy dodając do siebie momenty mas i dzieląc wynik przez masę układu m = m₁ + m₂.

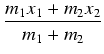
W ogólności, jeśli roważymy układ n obiektów o masach m₁, m₂,..., m_n umieszczonych w punktach x₁, x₂,..., x_n na osi x, to możemy pokazać, że centrum masy rozważanego układu umieszczone jest w punkcie

$$\overline{{x}}$$ = $${\frac{{\sum_{i=1}^n m_i x_i}}{{\sum_{i=1}^n m_i}}}$$ = $${\frac{{\sum_{i=1}^n m_i x_i}}{{m}}}$$

gdzie m = $\sum_{{i=1}}^{n}$m_i jest masą całego układu. Suma składowych momentów

M = $$\sum_{{i=1}}^{n}$$m_ix_i

nazywana jest momentem układu względem początku układu współrzędnych. Równanie wcześniejsze możemy zatem przepisać jako m$\overline{{x}}$ = M, co oznacza, że jeśli całkowitą masę układu skoncentrujemy w środku masy układu, to moment tej masy równy będzie momentowi całego układu.

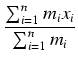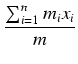
Rozważmy teraz układ n obiektów o masach m₁, m₂,..., m_n umieszczonych na płaszczyźnie w punktach o współrzędnych (x₁, y₁),(x₂, y₂),...,(x_n, y_n).

Poprzez analogię z przypadkiem jednowymiarowym możemy zdefiniować moment układu względem osi y jako sumę

M_y = $$\sum_{{i=1}}^{n}$$m_ix_i

oraz moment układu względem osi x jako sumę

M_x = $$\sum_{{i=1}}^{n}$$m_iy_i.

Moment M_y dostarcza nam informacji o tendencji układu do obracania się względem osi y, zaś moment M_x o tendencji do obracania się względem osi x.

Tak jak w przypadku jednowymiarowym, współrzędne ($\overline{{x}}$,$\overline{{y}}$) środka masy możemy wyrazić poprzez momenty za pomocą wzorów

$\overline{{x}}$ = ${\frac{{M_y}}{{m}}}$ oraz $\overline{{y}}$ = ${\frac{{M_x}}{{m}}}$,

gdzie m = $\sum_{{i=1}}^{n}$m_i jest masą całego układu. Ponieważ m$\overline{{x}}$ = M_y oraz m$\overline{{y}}$ = M_x, środek masy ($\overline{{x}}$,$\overline{{y}}$) jest punktem w którym pojedyncza cząsteczka ma takie same momenty względem wszystkich obiektów składających się na system.

W dalszym ciągu rozważmy płaską płytę o stałej gęstości $\rho$, będącą wycinkiem $\mathcal {R}$ płaszczyzny. Będziemy chcieli wyznaczyć środek masy płyty. Skorzystamy z następującej zasady: jeśli płyta $\mathcal {R}$ ma oś symetrii l, to środek masy leży na osi l. W szczególności wynika stąd, że środek masy prostokąta położony jest w jego środku. Momenty powinny być zdefiniowane w ten sposób, aby pozostały nie zmienione przy przemieszczeniu całej masy układu do środka masy. Ponadto moment dwóch rozłącznych układów był sumą momentów każdego z nich.

Przypuśćmy, że obszar $\mathcal {R}$ jest częścią płaszczyzny leżącą pomiędzy prostymi x = a, x = b, osią x i pod wykresem ciągłej funkcji f o nieujemnych wartościach.

Dzielimy przedział [a, b] na n podprzedziałów o końcach w punktach x₀, x₁,..., x_n i jednakowej szerokości $\Delta$x. W każdym z podprzedziałów wybieramy punkt próbkujący x_i^* w ten sposób, aby był środkiem $\overline{{x}}_{i}^{}$ i-tego podprzedziału, czyli aby $\overline{{x}}_{i}^{}$ = ${\frac{{x_{i-1} + x_i}}{{2}}}$. W ten sposób przybliżamy nasz obszar za pomocą wielokąta. Środek masy i-tego aproksymującego prostokąta R_i znajduje się w jego geometrycznym środku C_i($\overline{{x}}_{i}^{}$,${\frac{{1}}{{2}}}$f ($\overline{{x}}_{i}^{}$)). Pole owego prostokąta wynosi f ($\overline{{x}}_{i}^{}$)$\Delta$x, a więc jego masa wyraża się wzorem

$$\rho$$f ($$\overline{{x}}_{i}^{}$$)$$\Delta$$x.

Moment prostokąta R_i względem osi y jest iloczynem jego masy i odległości środka masy C_i od osi y, która wynosi $\overline{{x}}_{i}^{}$. Zatem

M_y(R_i) = [$$\rho$$f ($$\overline{{x}}_{i}^{}$$)$$\Delta$$x]$$\overline{{x}}_{i}^{}$$ = $$\rho$$$$\overline{{x}}_{i}^{}$$f ($$\overline{{x}}_{i}^{}$$)$$\Delta$$x.

Dodając do siebie te momenty otrzymujemy w rezultacie moment aproksymującego wielokąta. Zwiększając n otrzymujemy coraz to lepsze przybliżenia, tak więc ostatecznie moment płyty $\mathcal {R}$ względem osi y równy jest

M_y = $$\lim_{{n \rightarrow \infty}}^{}$$$$\sum_{{i=1}}^{n}$$$$\rho$$$$\overline{{x}}_{i}^{}$$f ($$\overline{{x}}_{i}^{}$$)$$\Delta$$x = $$\rho$$$$\int_{a}^{b}$$xf (x)dx.

W podobny sposób możemy obliczyć moment prostokąta R_i względem osi x jako iloczyn jego masy i odległości punktu C_i od osi x:

M_x(R_i) = [$$\rho$$f ($$\overline{{x}}_{i}^{}$$)$$\Delta$$x]$${\frac{{1}}{{2}}}$$f ($$\overline{{x}}_{i}^{}$$) = $$\rho$$$${\frac{{1}}{{2}}}$$[f ($$\overline{{x}}_{i}^{}$$)]²$$\Delta$$x.

Dodając do siebie rozważane momenty, a następnie przechodząc do granicy otrzymujemy wzór na moment płyty $\mathcal {R}$ względem osi x:

M_x = $$\lim_{{n \rightarrow \infty}}^{}$$$$\sum_{{i=1}}^{n}$$$$\rho$$$${\frac{{1}}{{2}}}$$[f ($$\overline{{x}}_{i}^{}$$)]²$$\Delta$$x = $$\rho$$$$\int_{a}^{b}$$$${\frac{{1}}{{2}}}$$[f (x)]²dx.

Tak jak w przypadku rozważanych wcześniej układów, środek masy zdefiniujemy w ten sposób, aby m$\overline{{x}}$ = M_y oraz m$\overline{{y}}$ = M_y. Aby obliczyć masę m płyty $\mathcal {R}$ musimy pomnożyć jej gęstość przez jej powierzchnię:

m = $$\rho$$A = $$\rho$$$$\int_{a}^{b}$$f (x)dx

i tym samym otrzymujemy

$$\overline{{x}}$$ = $${\frac{{M_y}}{{m}}}$$ = $${\frac{{\rho \int_a^b x f(x) dx}}{{\rho \int_a^b f(x) dx}}}$$ = $${\frac{{\int_a^b x f(x) dx}}{{\int_a^b f(x) dx}}}$$,

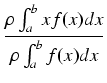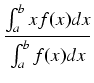$$\overline{{y}}$$ = $${\frac{{M_x}}{{m}}}$$ = $${\frac{{\rho \int_a^b \frac{1}{2} [f(x)]^2 dx}}{{\rho \int_a^b f(x) dx}}}$$ = $${\frac{{\int_a^b \frac{1}{2} [f(x)]^2 dx}}{{\int_a^b f(x) dx}}}$$.

Czytelnik zechce zwrócić uwagę, że gęstość $\rho$ uległa uproszczeniu. Tym samym położenie środka masy nie zależy od stałej gęstości płyty.

Przykład: Wyznaczyć środek masy płyty w kształcie półkola o promieniu r.

Aby móc zastosować wyprowadzone wcześniej wzory, umieszczamy płytę w układzie współrzędnych w ten sposób, aby środek koła, którego jest wycinkiem, znajdował się w początku układu współrzędnych, a górna krawędź opisana była równaniem f (x) = $\sqrt{{r^2 - x^2}}$, - r $\leq$ x $\leq$ r. Wyznaczenie współrzędnej $\overline{{x}}$ środka masy jest proste, wiemy bowiem, że środek masy musi być położony na osi symetrii płyty, a więc $\overline{{x}}$ = 0. Również pole A = $\int_{a}^{b}$f (x)dx nie wymaga obliczeń, wiemy bowiem że A = ${\frac{{1}}{{2}}}$$\pi$r². Tym samym:

$$\overline{{y}} {\frac{{1}}{{A}}} \int_{{-r}}^{r} {\frac{{1}}{{2}}}$$ =

$${\frac{{1}}{{\pi r^2/2}}} {\frac{{1}}{{2}}} \int_{{-r}}^{r} \sqrt{{r^2 - x^2}}$$ =

$${\frac{{2}}{{\pi r^2}}} \int_{0}^{r} {\frac{{2}}{{\pi r^2}}} {\frac{{x^3}}{{3}}}$$ =

$${\frac{{2}}{{\pi r^2}}} {\frac{{2r^3}}{{3}}} {\frac{{4 r}}{{3 \pi}}}$$ =

Tym samym współrzędne środka masy płyty to (0,${\frac{{4r}}{{3 \pi}}}$).

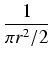Jeśli obszar $\mathcal {R}$ położony jest pomiędzy krzywymi y = f (x) i y = g(x), gdzie f (x) $\geq$ g(x), to rozumując w sposób analogiczny do powyższego możemy udowodnić, że środek masy płyty $\mathcal {R}$ ma współrzędne

$\overline{{x}}$ = ${\frac{{1}}{{A}}}$$\int_{a}^{b}$x[f (x) - g(x)]dx oraz $\overline{{y}}$ = ${\frac{{1}}{{A}}}$$\int_{a}^{b}$${\frac{{1}}{{2}}}${[f (x)]² - [g(x)]²}dx,

gdzie A oznacza pole powierzchni płyty $\mathcal {R}$.

Na zakończenie udowodnimy następujące twierdzenie, po raz pierwszy odkryte przez Pappusa z Aleksandrii w IV w. n. e.

Twierdzenie (Pappus): Niech $\mathcal {R}$ będzie obszarem leżącym całkowicie po jednej stronie prostej l na płaszczyźnie. Objętość bryły otrzymanej przez obrót $\mathcal {R}$ wokół osi l równa jest iloczynowi pola A obszaru $\mathcal {R}$ i drogi, jaką zatoczył środek masy płyty $\mathcal {R}$.

Dowód: Twierdzenie udowodnimy w przypadku, gdy opisywany obszar położony jest między krzywymi y = f (x) i y = g(x), gdzie f (x) $\geq$ g(x), a $\leq$ x $\leq$ b oraz oś l pokrywa się z osią y. Obliczając objętość bryły obrotowej za pomocą pierścieni cylindrycznych otrzymujemy

$$\int_{a}^{b} \pi$$ V =

$$\pi \int_{a}^{b}$$ =

$$\pi \overline{{x}}$$ =

$$\pi \overline{{x}}$$ =

gdzie d = 2$\pi$$\overline{{x}}$ jest drogą przebytą przez środek masy podczas pełnego obrotu.