


Next: Momenty i środki mas
Up: Rachunek całkowy
Previous: Powierzchnie brył obrotowych
Rozważmy cienką, poziomą płytę o polu powierzchni A, która jest zanurzona w cieczy o gęstości
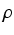 kg/m3 na głębokości d metrów poniżej poziomu cieczy.
Ciecz znajdująca się nad rozważaną płytą ma objętość V = Ad, a więc jej masa wynosi
m =
kg/m3 na głębokości d metrów poniżej poziomu cieczy.
Ciecz znajdująca się nad rozważaną płytą ma objętość V = Ad, a więc jej masa wynosi
m = 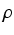 V =
V = 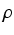 Ad. Siła wywierana przez ciecz na płytę wynosi zatem
Ad. Siła wywierana przez ciecz na płytę wynosi zatem
F =
mg =
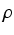 gAd
gAd
gdzie g jest stałym przyspieszeniem grawitacyjnym. Ciśnienie wywierane przez ciecz na płytę
definiujemy jako
P =
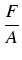
=
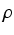 gd
gd.
Jednostką ciśnienia jest paskal,
1Pa = 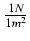 . Ważną właściwością ciśnienia (zaobserwowaną
doświadczalnie) jest fakt, że w dowolnym punkcie ciśnienie wywierane przez ciecz jest takie samo, bez
względu na kierunek. Wobec tego ciśnienie w każdym kierunku na głebokości d wywierane przez ciecz o
gęstości
. Ważną właściwością ciśnienia (zaobserwowaną
doświadczalnie) jest fakt, że w dowolnym punkcie ciśnienie wywierane przez ciecz jest takie samo, bez
względu na kierunek. Wobec tego ciśnienie w każdym kierunku na głebokości d wywierane przez ciecz o
gęstości 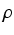 wynosi
wynosi
P =
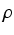 gd
gd.
Powyższa obserwacja pozwala nam obliczać ciśnienie działające na płyty zanurzone w cieczy w dowolny sposób
- a więc niekoniecznie poziomo, ale też pionowo, ukoośnie itp.
Przykład: Tama ma kształt trapezu. Jej wysokość wynosi 20 m, szerokość u góry 50 m, a u podstawy
30 m. Obliczyć siłę, z jaką woda napiera na tamę, jeżeli woda utrzymuje się na poziomie 4 m poniżej
szczytu tamy.
Dla ułatwienia obliczeń umieśćmy tamę w układzie współrzędnych, którego oś x ma kierunek pionowy,
zwrot skierowany ku dołowi i początek na poziomie lustra wody.
Głebokość wody wynosi 16 m, podzielmy zatem przedział [0, 16] na n podprzedziałów o równych długościach
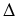 x i o końcach wyznaczonych przez punkty xi. Wybierzmy punkty próbkujące
xi*
x i o końcach wyznaczonych przez punkty xi. Wybierzmy punkty próbkujące
xi* 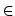 [xi-1, xi]. W ten sposób dzielimy powierzchnię tamy, na którą napiera woda na poziome paski,
z których każdy może być przybliżony prostokątem o wysokości
[xi-1, xi]. W ten sposób dzielimy powierzchnię tamy, na którą napiera woda na poziome paski,
z których każdy może być przybliżony prostokątem o wysokości 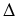 x i szerokości wi. Rozpatrując
odpowiednie trójkąty podobne dostajemy
x i szerokości wi. Rozpatrując
odpowiednie trójkąty podobne dostajemy
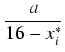
=
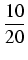
lub inaczej
a =
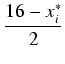
= 8 -
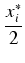
i wobec tego
wi = 2(15 +
a) = 2(15 + 8 -
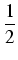 xi*
xi*) = 46 -
xi*.
Jeśli zatem Ai oznacza pole i-tego paska, to możemy je przybliżyć według wzoru
W przypadku, gdy 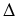 x jest odpowiednio małe, możemy założyć, że ciśnienie wywierane na i-ty pasek
jest stałe i wynosi
x jest odpowiednio małe, możemy założyć, że ciśnienie wywierane na i-ty pasek
jest stałe i wynosi
Pi 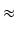
1000
gxi*.
Siła działająca na i-ty pasek jest iloczynem ciśnienia i powierzchni:
Fi =
PiAi 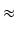
1000
gxi*(46 -
xi*)
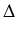 x
x.
Dodając do siebie wszystkie siły działające na wszystkie paski, a następnie zmierzając z n do
nieskończoności (i tym samym biorąc coraz węższe paski) otrzymujemy wzór na całkowitą siłę działającą
na tamę:
| F |
= |
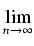 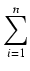 1000gxi*(46 - xi*) 1000gxi*(46 - xi*)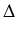 x = x = |
|
| |
= |
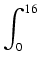 1000gx(46 - x)dx = 1000gx(46 - x)dx = |
|
| |
= |
1000(9, 8)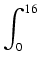 (46x - x2)dx = (46x - x2)dx = |
|
| |
= |
9800[23x2 - 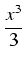 ]|016 = ]|016 = |
|
| |
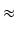 |
4, 43 . 107N |
|



Next: Momenty i środki mas
Up: Rachunek całkowy
Previous: Powierzchnie brył obrotowych
Pawel Gladki
2006-01-30
![]() kg/m3 na głębokości d metrów poniżej poziomu cieczy.
Ciecz znajdująca się nad rozważaną płytą ma objętość V = Ad, a więc jej masa wynosi
m =
kg/m3 na głębokości d metrów poniżej poziomu cieczy.
Ciecz znajdująca się nad rozważaną płytą ma objętość V = Ad, a więc jej masa wynosi
m = ![]() V =
V = ![]() Ad. Siła wywierana przez ciecz na płytę wynosi zatem
Ad. Siła wywierana przez ciecz na płytę wynosi zatem
![\includegraphics[width=12cm]{562-2.eps}](img856.gif)
![\includegraphics[width=12cm]{562-3.eps}](img857.gif)
![]() x i o końcach wyznaczonych przez punkty xi. Wybierzmy punkty próbkujące
xi*
x i o końcach wyznaczonych przez punkty xi. Wybierzmy punkty próbkujące
xi* ![]() [xi-1, xi]. W ten sposób dzielimy powierzchnię tamy, na którą napiera woda na poziome paski,
z których każdy może być przybliżony prostokątem o wysokości
[xi-1, xi]. W ten sposób dzielimy powierzchnię tamy, na którą napiera woda na poziome paski,
z których każdy może być przybliżony prostokątem o wysokości ![]() x i szerokości wi. Rozpatrując
odpowiednie trójkąty podobne dostajemy
x i szerokości wi. Rozpatrując
odpowiednie trójkąty podobne dostajemy
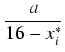 =
= 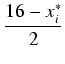 = 8 -
= 8 -