


Next: Uwagi historyczne o wzorach
Up: Wzory na pierwiastki wielomianów
Previous: Wielomiany stopnia 3 -
Równanie
ax4 + bx3 + cx2 + dx + e = 0 podstawieniem
x = y - b/(4a) sprowadza się do równania
postaci
y4 + py2 + qy + r = 0. Metoda Ferrari polega na wyrażeniu rozwiązań równania
y4 + py2 + qy + r = 0 przez
pierwiastki odpowiednio dobranego wielomianu stopnia 3:
y1 =
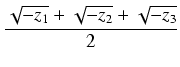
,
y2 =
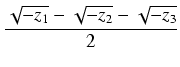
,
y3 =
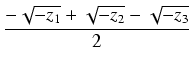
,
y4 =
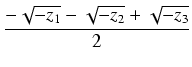
,
gdzie
z1, z2, z3 są rozwiązaniami równania
z3 -2pz2 + (p2 -4r)z + q2 = 0.
Odwrotnie,
z1, z2, z3 wyrażają się przez
y1, y2, y3, y4:
z1 = (y1 + y2)(y3 + y4),
z2 = (y1 + y3)(y2 + y4),
z3 = (y1 + y4)(y2 + y3)
i są niezmiennikami działania czteroelementowej podgrupy normalnej V4 grupy Galois S4 ogólnego
wielomianu stopnia 4. Każda grupa czteroelementowa ma dwuelementową podgrupę normalną i
S4/V4 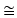 S3
(co oznacza, że równanie stopnia 4 sprowadza się do równania stopnia 3 i wyciągania pierwiastków
kwadratowych). Grupa S3 ma trzyelementową podgrupę normalną A3, więc V4 jest normalną podgrupą
dwunastoelementowej podgrupy normalnej grupy S4, która ma 24 elementy.
S3
(co oznacza, że równanie stopnia 4 sprowadza się do równania stopnia 3 i wyciągania pierwiastków
kwadratowych). Grupa S3 ma trzyelementową podgrupę normalną A3, więc V4 jest normalną podgrupą
dwunastoelementowej podgrupy normalnej grupy S4, która ma 24 elementy.
Wyróżnik
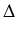
= 256
r3 -128
r2p2 +16
rp4 +144
prq2 -27
q4 -4
q2p3
wielomianu
z3 -2pz2 + (p2 -4r)z + q2 jest równy wyróżnikowi wielomianu
y4 + py2 + qy + r bo
(y4 - y1)(y3 - y2) = z2 - z1,
(y3 - y1)(y4 - y2) = z3 - z1,
(y2 - y1)(y4 - y3) = z3 - z2.



Next: Uwagi historyczne o wzorach
Up: Wzory na pierwiastki wielomianów
Previous: Wielomiany stopnia 3 -
Pawel Gladki
2006-01-30
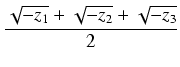 ,
,
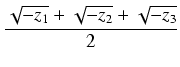 ,
,
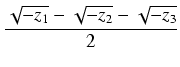 ,
,
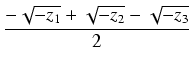 ,
,
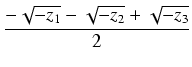 ,
,