

Jest rok 1535.
W Anglii rok temu król Henryk VIII Tudor ogłosił się głową kościoła w swoim królestwie. We Francji włada Franciszek I de Valois. Michał de Montaigne, później słynny filozof i erudyta, który po studiach prawniczych będzie zajmował wysokie stanowiska w polityce i administracji, zarządzał dużym majątkiem, bez żenady przyzna w swoich "Próbach" (Ksiega II), że "Otóż nie umiem rachować ani na żetonach, ani piórem", ma dwa lata. "Ojciec algebry" Francois Viéte urodzi się za pięć lat. W Niemczech Marcin Luter, obłożony klątwą przed 14 laty, napisał już swoje główne dzieła. Krzysztof Rudolf z Jawora, prywatny nauczyciel matematyki w Wiedniu, reprezentant szkoły coss, który 10 lat temu wydał w Strassbourgu podręcznik algebry, wprowadził właśnie oznaczenie pierwiastka stopnia 2 i 3, które w przyszłości Rene Descartes zmodyfikuje do dziesiejszego wyglądu. 13 lat temu Magellan opłynął Ziemię, trzy lata temu Hiszpanie zdobyli Peru, kładąc kres panowaniu Atahualpy i rozpoczynając bezprecedensowe ludobójstwo. Leonardo da Vinci zmarł 26 lat temu. Michelangelo Buonarotti w Rzymie poświęca się architekturze. Polska przeżywa Złoty Wiek pod rządami Zygmunta I Starego. Mikołaj Kopernik we Fromborku pełni różne funkcje administracyjne w kapitule warmińskiej. Mikołaj Rej osiadł w ziemi chełmińskiej, a Jan Kochanowski ma pięć lat. Tomasz Kłos pisze swoje "Algoritmus, to jest nauka liczby polską rzeczą", który ukaże się za trzy lata w oficynie Unglera. W Genewie Jan Kalwin ciska gromy na przeciwne Bogu prawa polskie, które każdemu pozwalają wierzyć, w co mu się podoba.
Od 41 lat "Summa de arithmetica, geometria, proporzioni di proporzionalita", fra Luca Paccioli di Burgo - mnicha-franciszkanina, wykładowcy matematyki uniwersytetów w Rzymie, Neapolu, Florencji, Bolonii i Wenecji - pierwszy wydrukowany (a nie przepisywany ręcznie) podręcznik matematyki, pozwala każdemu studentowi włoskiego uniwersytetu zapoznać się ze sztuką rozwiązywania równań, odziedziczoną po arabskich mistrzach (warto pamiętać, że w Anglii, Francji czy Niemczech uniwersytecka matematyka kończyła się na dodawaniu i odejmowaniu na palcach - aż do XVIII wieku!). Jest to pierwsze po "Liber abaci" Fibonacciego z 1202 roku podsumowanie całości wiedzy matematycznej (trzy rozdziały poświęcone były handlowi, buchalterii, pieniądzowi i wymianie). Sam Paccioli w latach 1469 - 1499 blisko współpracował z Leonardo da Vinci, pod którego wpływem napisał szereg prac z geometrii; w szczególności "De divina proportione" (Venezia 1509, Milano 1956) o złotym podziale, przedstawiająca 12 ciekawych własności złotego podziału, miała ilustracje Leonarda da Vinci. W 1509 Paccioli wydał "Elementy" Euklidesa po włosku.
W tym czasie sztuka rozwiązywania równań jest skomplikowana - nie ma symboli matematycznych, równanie x3 + 5x = 12 zapisuje się:
Jest rok 1535. Oto uniwersytet w Weronie szuka profesora matematyki. Po nowym roku ogłoszona zostaje publiczna dysputa połączona z turniejem matematycznym - uczestnicy będą zadawać sobie nawzajem zadania, wygra ten, kto rozwiąże więcej. Nie znano wtedy piłki nożnej i uważano za ciekawe takie zawody, a ich zwycięzców honorowano tak, jak teraz mistrzów kopania piłki. Fiori, który poza tym wydarzeniem nie zapisał się w historii, opracował 30 zadań, sprowadzających się do równań typu x3 + px = q. Nie zdało się to na nic: do dysputy i turnieju stanął Niccolo Fontana z Brescii, zwany Tartaglia ("Jąkała") (ok. 1500 - 13 XII 1557) - syn biednego gońca poczty konnej; w dzieciństwie ranny w gardło, gdy Francuzi zajęli Brescię - mówił z trudem, skąd wzięło się przezwisko; sam nauczył się czytania i pisania, łaciny i greki oraz matematyki (po śmierci ojca matka wysłała go do szkoły, ale pieniędzy zabrakło, gdy nauka doszła do litery "k"). Tartaglia początkowo uważał, że Fiori sam nie umie rozwiązać podanych zadań (bo w swej książce Paccioli otwarcie stwierdził, że nie ma ogólnego wzoru na rozwiązania takich równań). Na osiem dni przed terminem Tartaglia odkrył metodę rozwiązywania równań trzeciego stopnia i w dwie godziny rozwiązał zadnia, w wymaganym warunkami turnieju terminie 50 dni (tj. do 12 lutego) złożył rozwiązania u notariusza, a jego przeciwnik nie zdołał rozwiązać ani tych zadań Tartaglii, które sprowadzały się do równań postaci x3 = px + q, ani tego jednego, które sprowadzało się do równania objętego metodą del Ferro. Po tym wspaniałym zwycięstwie katedrę i wielką sławę zdobył Tartaglia - w dalszym ciągu publikował też prace z mechaniki, balistyki, geodezji i fortyfikacji. W 1537 wydał traktat "Nowa nauka", w którym udowodnił, że pocisk armatni poleci najdalej przy kącie podniesienia lufy 45 stopni. Napisał "Ogólny traktat o liczbie i mierze", wydany pośmiertnie - arytmetyka, algebra i geometria, oraz "Questioni et inventione diverse" (1547, "...nowe wynalazki, nie ukradzione Platonowi ni Plotynowi, a osiągniete tylko sztuką, pomiarem i rozumem") i "Cartelli di matematica disfida" (1547-48). Przetłumaczył na włoski dzieła Archimedesa i Euklidesa.
W 1539 roku pojawia się praca "Practica arithmeticae" słynnego lekarza i erudyty, Girolamo Cardano (24.IX.1501 - 21.IX.1576), w której autor wykazał się mistrzostwem w rozwiązywaniu równań, ale nie sformułował żadnej ogólnej metody. Cardano to syn znanego prawnika z Pawii, Fazio Cardano, matematyk, astrolog, filozof i lekarz, absolwent uniwersytetów w Pawii i Padwie. W młodości zajmował się wyłącznie medycyną, ale jako nieślubny syn nie mógł wstąpić do kolegium lekarskiego w Mediolanie, zanim (w sierpniu 1539 - specjalnie dla Cardano) nie zmieniono statutu. W 1534 został profesorem matematyki w Mediolanie; od 1547 profesor medycyny w Pawii i od 1562 - w Bolonii. Cardano był płodnym uczonym: opublikował około 200 prac różnych dziedzin (m. in. o teorii impetusu, zastosowaniu proporcji w fizyce, teorii dźwigni i wag, traktat "Practica arithmeticae" (1539), traktat "De Subtilitate", Norymberga 1550, traktat "De ludo aleae" (napisany w 1526, wydany w 1663) - O grze w kości, jedną z pierwszych w historii książek o rachunku prawdopodobieństwa). W 1545 opublikował traktat "Ars Magna, sive de regulis algebraicis", zawierający m. in.
Cardano jako jeden z pierwszych w Europie dopuszczał ujemne rozwiązania równań. Napisał też autobiografię "O moim życiu". "Opera" (Dzieła) Cardano w dziesięciu tomach wydano w 1663. Spis autorski wszystkich dzieł Cardano stanowił osobną ksiegę "O moich dziełach", ale w przededniu aresztowania w 1570 (przyczyna nieznana, przypuszczalnie Inkwizycja) Cardano spalił 120 własnych ksiąg.
Z racji rozległych zainteresowań Cardano jest jednym z niewielu matematyków znanych powszechnie, a nie tylko matematykom. Oto co napisał o nim w pierwszej polskiej encyklopedii "Nowe Ateny...", z lat 1745 - 1756, jej autor, ks. Benedykt Chmielowski:
Hieronymus CARDANUS z Mediolanu Xięstwa Włoskiego oriundus, Medyk i Matematyk sławny, powierzchowny Chrześcianin, a w sercu Ateusz. Nauczał w swych księgach blaspheme & impie, że Prawo starozakonne Żydowskie wyszło od Saturna. Nowy zaś Zakon, albo Ewangelia, od Jowisza i Merkuriusza; a zaś Alkoran Mahometa od Słońca i Marsa. Trzymał, że Świat ten jest wieczny; że człek pierwszy z zgnilizny się urodził, jako myszy albo żaby; że opętanych niemasz, ale to pochodzi z czarnej żółci, albo cholery. Czarta i Piekło policzył między bajki. Sam śmierci swojej prognostykował sobie czas; a że się tak nie weryfikowało, sam siebie głodem umorzył, aby się fałszywym nie pokazał Praktykarzem. Umierał na Świętym miejscu, utinam, świętobliwie, alias w Rzymie Roku 1576. Popisał Księgi Regulas Algebraicas, De consolatione Libros 3. De subtilitate Iibros 21, De Sapientia; ale te obie ostatnie zakazane czytać, póki by nie były purgowane.
Girolamo, albo Hieronymus Cardano był prawdziwym człowiekiem Renesansu, uczonym o wszechstronnych zainteresowaniach, godzącym niewolniczą wręcz zależność od Arystotelesa w fizyce i biologii z umiejętnością zerwania z wszelkimi tradycyjnymi uprzedzeniami co do liczb ujemnych, ba, do konsekwentnego posługiwania się pierwiastkami kwadratowymi z tych liczb. Był jednocześnie wspaniałym mechanikiem (sprzęgło Cardana) i zamiłowanym astrologiem. Podobno obok horoskopów Edwarda VI, Petrarki, Dürera, Vesaliego, Lutra ułożył nawet horoskop Chrystusa i przed stosem uchroniły go tylko układy w Watykanie na najwyższym szczeblu (z jego horoskopów korzystał papież). Opowiadają, że ułożył też własny horoskop, w którym przewidział datę własnej śmierci; kiedy ten dzień nadszedł, powiesił się, aby zachować sławę astrologa.
Opowiadają, że Cardano zaprosił do siebie Tartaglię, gościł go, obdarowywał, raczył smakołykami i pochlebstwami, aby wydobyć od niego jego metodę. Niccolo Tartaglia w końcu, odebrawszy od Cardano przysięgę dochowania tajemnicy, zdradził mu sposób rozwiązywania równania. Wzorując się na Boskiej Komedii Dantego podał ją w postaci wiersza, który (w wolnym przekładzie dra W. Więsława, "Matematyka i jej historia," Opole 1997) zaczyna się od słów
Kiedy sześcian z rzeczami razem
Równe są jakiejś liczbie,
Znajdą się dwie inne, na nią rozdzielające się...
Wiersz zawierał sposób znajdowania rozwiązywania równania x3 + px = q ("nie ma" liczb ujemnych!) w postaci x = u - v, gdzie u3 - v3 = q i u3v3 = (p/3)3 (zatem u3 i - v3 są dwoma pierwiastkami wielomianu z2 - q2z - (p/3)3) i sposób znajdowania rozwiązywania równania x3 = px + q w postaci x = u + v, gdzie u3 + v3 = q i u3v3 = (p/3)3 (zatem u3 i v3 są dwoma pierwiastkami wielomianu z2 - q2z + (p/3)3).
Podobno Tartaglia uzasadniał swoją metodę za pomocą geometrycznej interpretacji wzoru na sześcian sumy, znanego w tej formie już w starożytności.
Okazało się, że Cardano nie miał zamiaru dotrzymać przysięgi i zachować metody Tartaglii w tajemnicy. Cardano (który w tym czasie niewątpliwie był już najbardziej doświadczonym algebraikiem w Europie) pisał swoje największe dzieło, "Ars magna, sive de de regulis algebraicis" (Wielka sztuka, czyli o zasadach algebraicznych). Dla współczesnego czytelnika ta książka jest nudna (zdaniem Amy Dahan-Dalmédico i Jeanne Peiffer, "Routes et dédales", Paris 1982), bo - zmuszony do używania wyłącznie dodatnich współczynników - Cardano analizuje oddzielnie szereg typów równań drugiego i trzeciego stopnia. Przy okazji Cardano zauważył zadziwiającą własność metod Ferro i Tartaglii - tak zwany casus irreducibilis.
Przyjrzyjmy się wielomianowi (x + 1)(x + 2)(x - 3) = x3 - 7x - 6, który ma trzy pierwiastki rzeczywiste: -1, - 2, 3. Z XVI-wiecznego punktu widzenia równanie x3 - 7x - 6 = 0 ma jedno rozwiązanie x = 3. Zapiszemy równanie x3 - 7x - 6 = 0 w sposób XVI-wieczny:


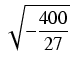
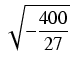
Cardano wpadł na pomysł, żeby dalej liczyć najzwyczajniej w świecie, nie zastanawiając się, co to jest
![]() , tylko przestrzegając praw działań:
, tylko przestrzegając praw działań:
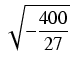
Łatwo zauważyć, że jeśli liczba
a + b![]() ma własność
ma własność
Cardano, który stosował podstawienia w rodzaju y = x - b/3a w równaniach postaci ax3 + bx2 + cx + d = 0, musiał uwzględniać ujemne rozwiązania równań - nazywał je liczbami fikcyjnymi lub "mniej czystymi pierwiastkami". Dlatego też łatwiej było zaakceptować wyrażenia typu
I w ten sposób pojawiły się liczby zespolone.
Po ukazaniu się drukiem "Ars magna" w 1545 Tartaglia poczuł się oszukany. Rozpoczął się wielki spór
o priorytet odkrycia. Tartaglia w 1546 wydał pracę "Questioni et inventione diverse" (Pytania
i rozmaite odkrycia), a potem (1547 - 1548) wymienił z Ferrari, uczniem Cardano, broszury zatytułowane
"Cartelli di matematica disfida" i spór między Tartaglią a Cardano przybrał publiczny charakter.
Tartaglia umarł w 1557. Uczeń Cardano, Raphaelo Bombelli postanowił napisać traktat o algebrze,
zawierający systematyczny wykład odkryć minionego półwiecza. Pierwsza wersja tego traktatu powstała
w latach 1557 - 1560. Ale gdy Bombelli zapoznał się z odnalezioną w Wenecji przez Regimontana "Arytmetyką"
Diofantosa, przeredagował swój traktat, m.in. włączając do niego około 140 zadań wziętych z "Arytmetyki".
Wprowadził również - wzorując się na Diofantosie - cztery rodzaje wielkości: piu - liczby rzeczywiste
dodatnie, meno - liczby rzeczywiste ujemne, piu di meno - wyrażenia postaci
a . ![]() =
= ![]() , gdzie a jest liczbą rzeczywistą dodatnią, oraz meno di meno
- wyrażenia postaci
- a .
, gdzie a jest liczbą rzeczywistą dodatnią, oraz meno di meno
- wyrażenia postaci
- a . ![]() = -
= - ![]() , gdzie a jest liczbą rzeczywistą dodatnią.
Sformułował wyraźnie (jak Diofantos dla liczb względnych) prawa działań na tych liczbach. Pierwsze trzy
księgi "L'Algebra" Bombellego (Bologna, 1579) ukazały się w 1572, parę miesięcy przed śmiercią autora. Bombelli
zauważył, że dwie metody Tartaglii i metoda del Ferro to jeden i ten sam wzór, podobnie jak dwadzieścia
kilka przypadków metody Ferrari to różne przypadki jednego wzoru. Bombelli podał przykład:
, gdzie a jest liczbą rzeczywistą dodatnią.
Sformułował wyraźnie (jak Diofantos dla liczb względnych) prawa działań na tych liczbach. Pierwsze trzy
księgi "L'Algebra" Bombellego (Bologna, 1579) ukazały się w 1572, parę miesięcy przed śmiercią autora. Bombelli
zauważył, że dwie metody Tartaglii i metoda del Ferro to jeden i ten sam wzór, podobnie jak dwadzieścia
kilka przypadków metody Ferrari to różne przypadki jednego wzoru. Bombelli podał przykład:
Podobno (J.J. O'Connor, E.F. Robertson, Quadratic, cubic and quartic equations) pierwszy algebraiczny dowód poprawności wzorów Cardano - obliczenie iloczynu