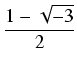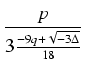Next: Wielomiany stopnia 4 -
Up: Wzory na pierwiastki wielomianów
Previous: Wielomiany stopnia 2
Z uwagi na znaczną komplikację wzorów dla równania
ax3 + bx2 + cx + d = 0
w pełnej postaci:
gdzie
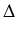
= - 4
c3a +
c2b2 +18
cbad - 27
d2a2 -4
db3
jest wyróżnikiem, równanie
ax3 + bx2 + cx + d = 0 dzielimy przez a znajdując równoważne równanie
x3 + (b/a)x2 + (c/a)x + (d /a) = 0, po czym podstawienie
x = y - b/(3a)
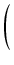 y - y - 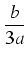 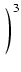 + +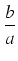 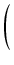 y - y - 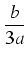 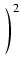 + +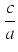 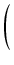 y - y - 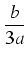 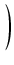 + +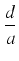 = = |
| |
= |
y3 - 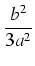 y + y + 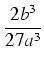 + + 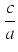 y - y - 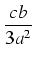 + + 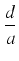 = = |
|
| |
= |
y3 + 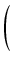 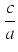 - - 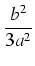 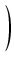 y - y - 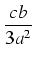 + + 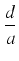 + + 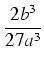 |
|
sprowadza równanie do postaci
y3 + py + q = 0, i znajdujemy rozwiązania z wzorów Cardano:
gdzie
D = - 4p3 -27q2
jest wyróżnikiem.
Jeśli nie mamy ochoty uczyć się tych wzorów, to - metodą Thomasa Harriota - w równaniu
y3 + py + q = 0
podstawiamy
y = z - p/(3z):
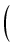 z
z -
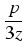
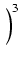
+
p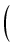 z
z -
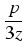
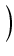
+
q =
z3 -
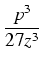
+
q
i t = z3 znajdujemy, rozwiązując równanie
t2 +
qt -
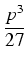
= 0



Next: Wielomiany stopnia 4 -
Up: Wzory na pierwiastki wielomianów
Previous: Wielomiany stopnia 2
Pawel Gladki
2006-01-30
![$\displaystyle \sqrt[3]{{\frac{9cba-27da^2-2b^3+3a\sqrt{-3\Delta}}{2a^3}}}$](img1134.gif)
![$\displaystyle {\frac{{3ca-b^2}}{{3a^2 \sqrt[3]{\frac{9cba-27da^2-2b^3+3a\sqrt{-3\Delta}}{2a^3}}}}}$](img1136.gif)
![$\displaystyle \sqrt[3]{{\frac{9cba-27da^2-2b^3+3a\sqrt{-3\Delta}}{2a^3}}}$](img1134.gif)
![$\displaystyle {\frac{{3ca-b^2}}{{3a^2 \sqrt[3]{\frac{9cba-27da^2-2b^3+3a\sqrt{-3\Delta}}{2a^3}}}}}$](img1136.gif)
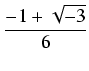
![$\displaystyle \sqrt[3]{{\frac{9cba-27da^2-2b^3+3a\sqrt{-3\Delta}}{2a^3}}}$](img1134.gif)
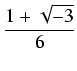
![$\displaystyle {\frac{{3ca-b^2}}{{a^2 \sqrt[3]{\frac{9cba-27da^2-2b^3+3a\sqrt{-3\Delta}}{2a^3}}}}}$](img1142.gif)
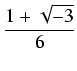
![$\displaystyle \sqrt[3]{{\frac{9cba-27da^2-2b^3+3a\sqrt{-3\Delta}}{2a^3}}}$](img1134.gif)
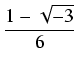
![$\displaystyle {\frac{{3ca-b^2}}{{a^2 \sqrt[3]{\frac{9cba-27da^2-2b^3+3a\sqrt{-3\Delta}}{2a^3}}}}}$](img1142.gif)
![$\displaystyle \sqrt[3]{{\frac{-9q + \sqrt{-3\Delta}}{18}}}$](img1157.gif)
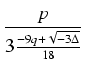
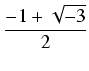
![$\displaystyle \sqrt[3]{{\frac{-9q + \sqrt{-3\Delta}}{18}}}$](img1157.gif)
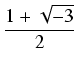
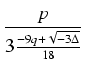
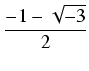
![$\displaystyle \sqrt[3]{{\frac{-9q + \sqrt{-3\Delta}}{18}}}$](img1157.gif)