Związki między funkcjami trygonometrycznymi tego samego kąta skierowanego

Trzy podstawowe tożsamości między funkcjami trygonometrycznymi tego samego kąta skierowanego ujmują wzory:

sin²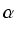$$\alpha$$ + cos²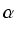$$\alpha$$ = 1,

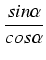
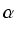
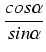
$${\frac{{sin \alpha}}{{cos \alpha}}}$$ = tg$$\alpha$$,

$${\frac{{cos \alpha}}{{sin \alpha}}}$$ = ctg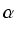$$\alpha$$.

Pierwszy ze wzorów nosi nazwę jedynki trygonometrycznej.

Dowód: Sprowadzając kąt 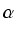$\alpha$ do położenia standardowego otrzymujemy:

Między x, y, r zachodzi związek x² + y² = r². Dzieląc tę równość przez r² i uwzględniając definicje funkcji trygonometrycznych otrzymujemy jedynkę trygonometryczną. Pozostałe dwa wzory dowodzimy w podobnie prosty sposób.