Trysekcja kąta

Niemożliwe jest podanie metody podzielenia cyrklem i linijka dowolnego kąta na trzy równe części. Kąty dzielą się na takie, które da się podzielić na trzy części cyrklem i linijką (np. 90°), oraz na takie, których cyrklem i linijką nie da się podzielić na trzy równe części (np. 120°). Oczywiście, jeśli użyć odpowiednich narzędzi, to za ich pomocą można dokonać trysekcji dowolnego kąta (tzw. konstrukcja neusis - tak Dinostarates dokonał trysekcji za pomocą kwadratrysy). Dowód niewykonalności trysekcji wymaga narzędzi - punkty płaszczyzny trzeba zinterpretować jako liczby zespolone i wiedzieć co to jest ciało, rozszerzenie ciała oraz stopień rozszerzenia (a więc i wymiar przestrzeni wektorowej). Jak to się wie, to sprawa jest prosta - sprawdza się, że wszystkie punkty, które można zbudować z danego odcinka jednostkowego cyrklem i linijką odpowiadają liczbom zespolonym, które przy każdym kroku konstrukcji albo należały do już zbudowanego ciała, albo są pierwiastkami trójmianu kwadratowego (o współczynnikach z już zbudowanego ciała), czyli w każdym kroku konstrukcji nowe ciało jest albo tym samym co w poprzednim kroku, albo jego rozszerzeniem stopnia 2. Dlatego stopień rozszerzenia (Q(z) : Q) musi być potęgą dwójki dla każdego konstruowalnego punktu z. A istnieją kąty, przy trysekcji których trzeba zbudować punkt z, który jest pierwiastkiem nierozkładalnego wielomianu trzeciego stopnia. W takim przypadku (Q(z) : Q) = 3, i z konstruowalności z wynikałoby, że 3 jest dzielnikiem potęgi dwójki.

Istnienie kątów, których konstrukcyjnie nie da się podzielić na trzy równe części pierwszy uzasadnił (w wieku 19 lat!) C. F. Gauss (1777-1855). Oto dwa fragmenty z Rozdziału VII jego "Disquisitiones Arithmeticae" (Lipsk 1801, za W. Więsław "Matematyka i jej historia", Opole 1997, str. 331-332), z dodanymi uwagami w nawiasach kwadratowych. Pierwszy zawiera rezultaty pozytywne:

365. Tym samym, przy pomocy poprzednich badań, sprowadziliśmy zagadnienie podziału koła na n części, gdzie n jest liczbą pierwszą, do rozwiązania równań, których liczba równa jest liczbie czynników [pierwszych], na które można rozłożyć liczbę n - 1, a stopnie wielomianów określone są przez liczbę [chyba raczej: wartość] czynników. Zatem, jesli n - 1 jest potęgą liczby 2, co ma miejsce dla wartości n = 3, 5, 17, 157, 65537,..., to podział koła sprowadza się do rozwiązania tylko równań kwadratowych, a funkcje trygonometryczne kątów P/n, 2P/n,... [Gauss oznacza literą P liczbę $\pi$] mogą być wyrażone przy pomocy bardziej lub mniej złożonych (w zależności od n) równań kwadratowych. A zatem, w tym przypadku podział koła na n części, czyli konstrukcja n-kąta foremnego, może być dokonana przy pomocy konstrukcji geometrycznych. Na przykład, dla n = 17, z art. 354, 361 łatwo wyznaczyć następujacy wzór na cosinus kata [2]P/17:

$${\frac{{\sqrt{17} - 1 + \sqrt{2(17 - \sqrt{17})} + 2 \sqrt{17 + 3 \sqrt{17} - \sqrt{2(17 - \sqrt{17})} - 2 \sqrt{2(17 + \sqrt{17})}}}}{{16}}}$$

Cosinusy wielokrotności tego kąta mają analogiczną postać, a sinusy zawierają o jeden radykał więcej. Jest godnym uwagi, że podczas, gdy możliwość geometrycznego dzielenia koła na trzy i pięć części była znana już w czasach Euklidesa, to w ciągu 2000 lat nie dodano do tych wyników nic nowego i że wszyscy matematycy uważali, że prócz wskazanych podziałów i tych, które otrzymuje się z nich bezpośrednio, a mianowicie podziałów na 15, 3 ^. 2m, 5 ^. 2m, 15 ^. 2m, i 2m części, żadne inne podziały nie są wykonalne przy pomocy konstrukcji geometrycznych. [...]

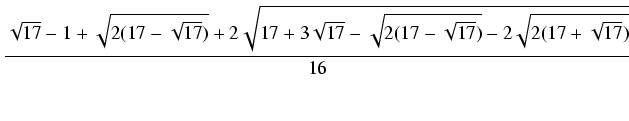
I rezultaty negatywne:

366. Jeśli trzeba dzielić koło na a^$\alpha$ części, gdzie a oznacza liczbę pierwszą, to rzecz jasna, zawsze można wykonać to geometrycznie, jeśli a = 2, ale dla żadnych innych wartości a nie jest to możliwe, jeśli tylko $\alpha$ > 1 [tu Gauss stwierdza m. in. niewykonalność konstrukcji dziewięciokąta foremnego i niemożliwość trysekcji kąta 120°]; istotnie, wówczas należałoby rozwiązać, prócz tych równań, które potrzebne są do dzielenia na a części, takze a - 1 innych równań, stopnia a; równania te nie mogą być pominięte ani ich stopnie obniżone. Stopnie tych równań (także dla $\alpha$ = 1) będą zawsze dzielnikami pierwszymi liczby (a - 1)a^$\alpha$ - 1.

Te uwagi Gaussa zamienił na ścisły dowód Pierre L. Wantzel (1814-1848) w 1837 r. Wantzel był repetytorem w École Polytechnique w Paryżu, tej samej, w której Evariste Galois dwukrotnie oblał egzamin wstępny: w 1828 (egzaminatorem był Lefebre) i w 1829 (egzaminatorem był Dinet). Sam Wantzel był postacią niezwykle barwną: wstąpił na Politechnikę w 1832 roku zajmując pierwszą lokatę. Jego wszechstronne studia i zainteresowania objęły, oprócz filozofii, matematykę, historię i muzykę. W 1843 został wykładowcą; potrafił pracować bez wytchnienia, bez snu i odpoczynku. Nieregularny tryb życia, kawa i opium, doprowadziły do jego przedwczesnej śmierci, prawdopodobnie w 1848 roku.