


Next: Metoda współczynników nieoznaczonych
Up: Rachunek całkowy
Previous: Całki funkcji zawierających pierwiastki
Opiszemy metodę całkowania funkcji zawierających pierwiastek z trójmianu kwadratowego. Pierwszym krokiem przy
rozwiązywaniu tegu typu całek jest zawsze sprowadzenie występującego tam trójmianu do postaci kanonicznej:
ax2 +
bx +
c =
a(
x +
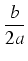
)
2 -
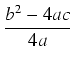
i wykonanie odpowiedniego podstawienia, dzięki któremu dalsze obliczenia sprowadzają się do znalezienia całki
z funkcji zawierającej wyrażenie jednego z trzech następujących typów:
Opiszemy metody całkowania w każdym z trzech przypadków z osobna.
Całki z funkcji zawierających wyrażenie
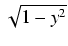 . Całki takie obliczamy stosując podstawienie:
. Całki takie obliczamy stosując podstawienie:
y = sin(t).
Wówczas
dy = cos(t)dt oraz
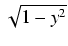 =
= 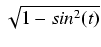 = cos(t).
= cos(t).
Przykład: Obliczyć całkę:
 x2
x2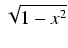 dx
dx.
Stosujemy podstawienie
x = sin(t), skąd
dx = cos(t)dt i otrzymujemy:
 x2 x2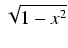 dx= dx= sin2(t)cos(t)cos(t)dt= sin2(t)cos(t)cos(t)dt= |
| |
= |
 (sin(t)cos(t))2dt = (sin(t)cos(t))2dt =  ( (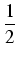 sin(2t))2dt = sin(2t))2dt = |
|
| |
= |
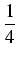  sin2(2t)dt = sin2(2t)dt = 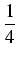  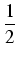 (1 - cos(4t))dt = (1 - cos(4t))dt = |
|
| |
= |
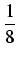 dt - dt - 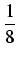  cos(4t)dt = cos(4t)dt = 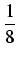 t - t - 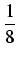 . . 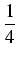 sin(4t) + C = sin(4t) + C = |
|
| |
= |
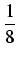 srcsin(x) - srcsin(x) - 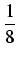 x(1 - 2x2) x(1 - 2x2)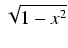 + C. + C. |
|
W ostatniej linijce zamieniliśmy nową zmnienną t na starą zmienną x - ten krok wymaga na ogół zastosowania
kilku sztuczek, które omówimy szczegółowo poniżej.
Całki z funkcji zawierających wyrażenie
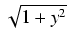 . Całki takie obliczamy stosując podstawienie:
. Całki takie obliczamy stosując podstawienie:
y = tg(t).
Wówczas
dy = 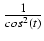 dt oraz
dt oraz
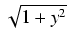 =
= 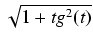 =
= 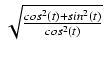 =
= 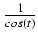 .
.
Przykład: Obliczyć całkę:

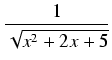 dx
dx.
Najpierw sprowadzamy trójmian do postaci kanonicznej:
Stosujemy podstawienie
y = 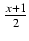 , skąd dx = 2dy:
a następnie omawiane podstawienie y = tg(t),
dy =
, skąd dx = 2dy:
a następnie omawiane podstawienie y = tg(t),
dy = 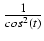 dt:
i dalej rozwiązujemy w oparciu o znane metody całkowania funkcji trygonometrycznych.
dt:
i dalej rozwiązujemy w oparciu o znane metody całkowania funkcji trygonometrycznych.
Całki z funkcji zawierających wyrażenie
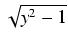 . Całki takie obliczamy stosując podstawienie:
. Całki takie obliczamy stosując podstawienie:
y =
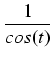
.
Wówczas
dy = 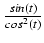 dt oraz
dt oraz
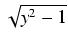 =
= 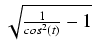 =
= 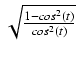 =
= 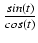 .
.
Przykład: Obliczyć całkę:

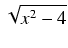 dx
dx.
Oczywiście:
stosujemy więc podstawienie
y = 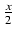 , skąd dx = 2dy:
a następnie omawiane podstawienie
y =
, skąd dx = 2dy:
a następnie omawiane podstawienie
y = 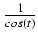 ,
dy =
,
dy = 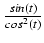 dt:
i dalej rozwiązujemy w oparciu o znane metody całkowania funkcji trygonometrycznych.
dt:
i dalej rozwiązujemy w oparciu o znane metody całkowania funkcji trygonometrycznych.
Przy obliczaniu całek omawianych typów najtrudniejszym fragmentem rozwiązania jest z reguły powrót do
oryginalnej zmiennej po przeprowadzeniu wszystkich całkowań: otrzymujemy w rezultacie funkcje zmiennej t,
które musimy wyrazić jako funkcje zmiennej y, przy czym y i t związane są pewnymi zależnościami trygonometrycznymi.
Omówimy ten problem na przykładzie podstawienia
u = sin(t). Jeżeli chcemy wyrazić t jako funkcję u,
to oczywiście
t = arcsin(u). Ale jak "zgrabnie" wyrazić cos(t), sin(t), tg(t) i ctg(t) jako funkcję u?
W większości przypadków pomocne jest posłużenie się odpowiednim rysunkiem:
Oczywiście
u = sin(t) i proste rachunki pozwalają sprawdzić, że:
cos(
t) =
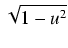
,
tg(
t) =
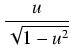
,
ctg(
t) =
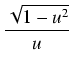
.
Podstawienia Eulera. Alternatywanym sposobem rozwiązywania opisywanych problemów jest zastosowanie
tzw. podstawień Eulera. Podstawienia te stodujemy bezpośrednio do pierwiastków z trójmianów, nie sprowadzając
ich wcześniej do postaci kanonicznej - czasami jest to pewne ułatwienie.
Jeżeli całkowana funkcja zawiera wyrażenie
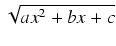 , to:
, to:
- jeśli a > 0, stosujemy pierwsze podstawienie Eulera:
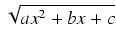
=
t -
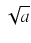 x
x;
- jeśli c > 0, stosujemy drugie podstawienie Eulera:
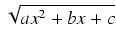
=
xt +
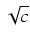
;
- jeśli wielomian pod pierwiastkiem ma rzeczywiste miejsca zerowe u, v, stosujemy trzecie podstawienie Eulera:
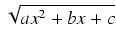
=
t(
x -
u).
Przykład: Obliczyć całkę:

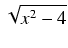 dx
dx.
Stosujemy pierwsze podstawienie Eulera:
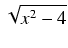
=
t -
x 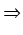 x2
x2 -4 =
t2 -2
tx +
x2 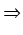
2
tx = 4 +
t2 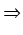 x
x =
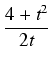
.
Wobec tego
dx = 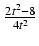 dt i otrzymujemy:
dt i otrzymujemy:
 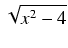 dx= dx= (t-x) (t-x)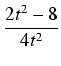 dt= dt= |
| |
= |
 (t - (t - 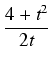 ) )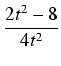 dt = dt =  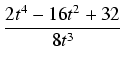 dt = dt = |
|
| |
= |
 ( (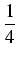 t - t - 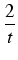 + + 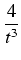 )dt = )dt = 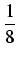 t2 -2ln| t| - t2 -2ln| t| - 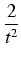 + C = + C = |
|
| |
= |
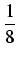 (x + (x + 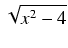 )2 -2ln| x + )2 -2ln| x + 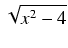 | - | - 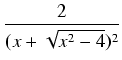 + C. + C. |
|
Czytelnik zechce zweryfikować, że rozwiązanie to jest o wiele krótsze od poprzedniego, z zastosowaniem podstawień
trygonometrycznych.
Ćwiczenia:
-

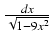 Odpowiedź:
Odpowiedź:
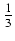 arcsin(3x) + C
arcsin(3x) + C
-

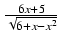 dx Odpowiedź:
-6
dx Odpowiedź:
-6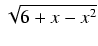 +8arcsin(
+8arcsin(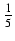 (2x - 1)) + C
(2x - 1)) + C
-

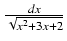 Odpowiedź:
ln| x +
Odpowiedź:
ln| x + 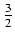 +
+ 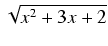 | + C
| + C
-

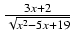 dx Odpowiedź:
3
dx Odpowiedź:
3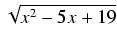 +
+ 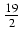 ln| x -
ln| x - 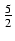 +
+ 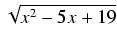 | + C
| + C
-

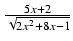 dx Odpowiedź:
dx Odpowiedź:
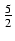
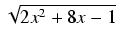 -4
-4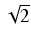 ln| x + 2 +
ln| x + 2 + 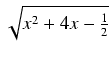 | + C
| + C
-

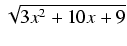 dx Odpowiedź:
dx Odpowiedź:
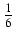 (3x + 5)
(3x + 5)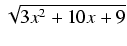 +
+ 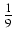
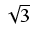 ln(3x + 5 +
ln(3x + 5 + 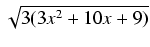 ) + C
) + C
-

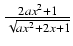 dx Odpowiedź:
(x -
dx Odpowiedź:
(x - 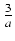 )
)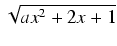 +
+ 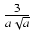 ln(ax + 1 +
ln(ax + 1 + 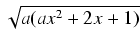 ) + C
) + C
-

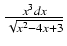 Odpowiedź:
Odpowiedź:
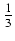 (x2 +5x + 24)
(x2 +5x + 24)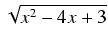 +11ln| x - 2 +
+11ln| x - 2 + 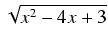 | + C
| + C
-

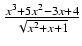 dx Odpowiedź:
(
dx Odpowiedź:
(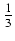 x2 +
x2 + 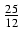 x -
x - 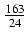 )
)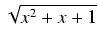 +
+ 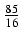 ln| x +
ln| x + 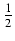 +
+ 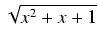 | + C
| + C
-

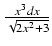 Odpowiedź:
Odpowiedź:
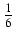 (x2 -3)
(x2 -3)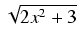 + C
+ C



Next: Metoda współczynników nieoznaczonych
Up: Rachunek całkowy
Previous: Całki funkcji zawierających pierwiastki
Pawel Gladki
2006-01-30
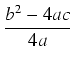
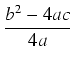
![]() . Całki takie obliczamy stosując podstawienie:
. Całki takie obliczamy stosując podstawienie:
![]() . Całki takie obliczamy stosując podstawienie:
. Całki takie obliczamy stosując podstawienie:
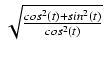 =
= 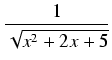 dx.
dx.
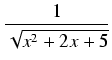 dx =
dx = 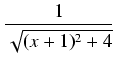 dx =
dx = 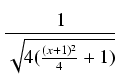 dx =
dx = 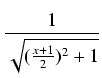 dx.
dx.
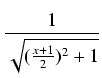 dx =
dx = 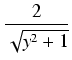 dy =
dy = 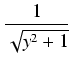 dy,
dy,
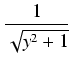 dy =
dy = 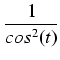 dt =
dt = 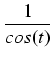 dt
dt
![]() . Całki takie obliczamy stosując podstawienie:
. Całki takie obliczamy stosując podstawienie:
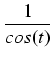 .
.
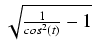 =
= 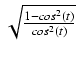 =
= 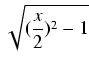 dx,
dx,
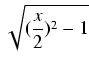 dx = 4
dx = 4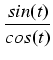
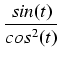 dt
dt

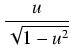 , ctg(t) =
, ctg(t) = 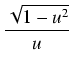 .
.
![]() , to:
, to:
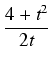 .
.
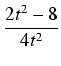 dt=
dt=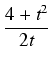 )
)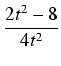 dt =
dt = 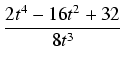 dt =
dt =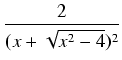 + C.
+ C.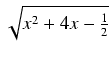 | + C
| + C