next up previous
Next: Liczba e Up: Liczby rzeczywiste Previous: Pi-ematy, czyli jak zapamiętać

Jak obliczyć log35?

Logarytmy przy różnych podstawach wyraża się przez logarytmy naturalne według wzoru

logab = $\displaystyle {\frac{{\ln b}}{{\ln a}}}$

Bezpośrednie obliczanie logarytmów naturalnych - za pomocą odkrytego przez Mikołaja Mercatora (Nicolaus Kaufman 1620-1687, nie mylić z kartografem Gerardem Mercatorem, czyli Gerhardem Kramerem 1512-1594) w książce "Logarytmotechnika" (Londyn, 1668) szeregu

ln(1 + x) = x - $\displaystyle {\frac{{x^2}}{{2}}}$ + $\displaystyle {\frac{{x^3}}{{3}}}$ - $\displaystyle {\frac{{x^4}}{{4}}}$ + $\displaystyle {\frac{{x^5}}{{5}}}$ -...

dla -1 < x $ \leq$ 1 jest raczej beznadziejne - nawet dla x = 2. Do praktycznego obliczania logarytmów naturalnych wykorzystuje się szereg Taylora:
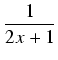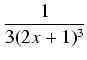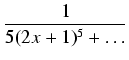ln$\displaystyle \left(\vphantom{ \frac{x+1}{x} }\right.$$\displaystyle {\frac{{x+1}}{{x}}}$$\displaystyle \left.\vphantom{ \frac{x+1}{x} }\right)$ = 2$\displaystyle \left(\vphantom{ \frac{1}{2x + 1} + \frac{1}{3(2x+1)^3} + \frac{1}{5(2x+1)^5 + \ldots} }\right.$$\displaystyle {\frac{{1}}{{2x + 1}}}$ + $\displaystyle {\frac{{1}}{{3(2x+1)^3}}}$ + $\displaystyle {\frac{{1}}{{5(2x+1)^5 + \ldots}}}$$\displaystyle \left.\vphantom{ \frac{1}{2x + 1} + \frac{1}{3(2x+1)^3} + \frac{1}{5(2x+1)^5 + \ldots} }\right)$ =  
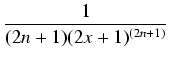  = 2$\displaystyle \sum_{{n=0}}^{{\infty}}$$\displaystyle {\frac{{1}}{{(2n+1)(2x+1)^{(2n+1)}}}}$  

zbieżmy dla (2x + 1)2 > 1. Logarytmy naturalne liczb naturalnych oblicza się rekurencyjnie: ln 1 = 0 i jesli znany jest ln N, to

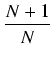
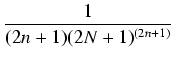
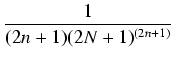ln(N + 1) - ln N = ln$\displaystyle \left(\vphantom{ \frac{N+1}{N} }\right.$$\displaystyle {\frac{{N+1}}{{N}}}$$\displaystyle \left.\vphantom{ \frac{N+1}{N} }\right)$ = 2$\displaystyle \sum_{{n=0}}^{{\infty}}$$\displaystyle {\frac{{1}}{{(2n+1)(2N+1)^{(2n+1)}}}}$

czyli:

ln(N + 1) = ln N + 2$\displaystyle \sum_{{n=0}}^{{\infty}}$$\displaystyle {\frac{{1}}{{(2n+1)(2N+1)^{(2n+1)}}}}$.

Dla N > 0 iloraz dwóch kolejnych składników spełnia nierówność:

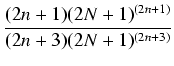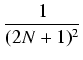
$\displaystyle {\frac{{(2n+1)(2N+1)^{(2n+1)}}}{{(2n+3)(2N+1)^{(2n+3)}}}}$ < $\displaystyle {\frac{{1}}{{(2N+1)^2}}}$ $\displaystyle \leq$ $\displaystyle {\frac{{1}}{{9}}}$

więc błąd wynikający z ograniczenia się do n składników szeregu wynosi:
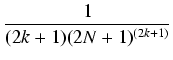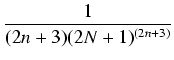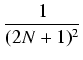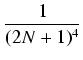2$\displaystyle \sum_{{k=n+1}}^{{\infty}}$$\displaystyle {\frac{{1}}{{(2k+1)(2N+1)^{(2k+1)}}}}$ < 2$\displaystyle {\frac{{1}}{{(2n+3)(2N+1)^{(2n+3)}}}}$$\displaystyle \left(\vphantom{ 1 + \frac{1}{(2N+1)^2} + \frac{1}{(2N+1)^4} + \ldots }\right.$1 + $\displaystyle {\frac{{1}}{{(2N+1)^2}}}$ + $\displaystyle {\frac{{1}}{{(2N+1)^4}}}$ +...$\displaystyle \left.\vphantom{ 1 + \frac{1}{(2N+1)^2} + \frac{1}{(2N+1)^4} + \ldots }\right)$ =  
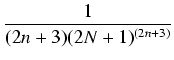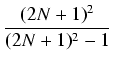  = 2$\displaystyle {\frac{{1}}{{(2n+3)(2N+1)^{(2n+3)}}}}$$\displaystyle {\frac{{(2N+1)^2}}{{(2N+1)^2 - 1}}}$ =  
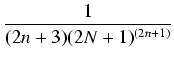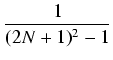  = 2$\displaystyle {\frac{{1}}{{(2n+3)(2N+1)^{(2n+1)}}}}$$\displaystyle {\frac{{1}}{{(2N+1)^2 - 1}}}$  

Żeby obliczyć ln 2 = ln(1 + 1) z dokładnością do 1000 miejsc po przecinku, trzeba dobrać n tak, żeby

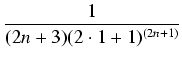
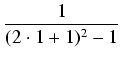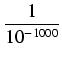
2$\displaystyle {\frac{{1}}{{(2n+3)(2 \cdot 1+1)^{(2n+1)}}}}$$\displaystyle {\frac{{1}}{{(2 \cdot 1+1)^2 - 1}}}$ < $\displaystyle {\frac{{1}}{{10^{-1000}}}}$

więc wystarczy 1050 składników. Obliczenie ln 3 = ln(2 + 1) z taką samą dokładnością wymaga zsumowania n skladników z

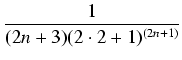
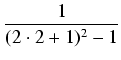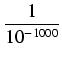
2$\displaystyle {\frac{{1}}{{(2n+3)(2 \cdot 2+1)^{(2n+1)}}}}$$\displaystyle {\frac{{1}}{{(2 \cdot 2+1)^2 - 1}}}$ < $\displaystyle {\frac{{1}}{{10^{-1000}}}}$

i wystarczy 715 składników. ln 4 = 2 ln 2 nie wymaga dodatkowych obliczeń, a aby obliczyć ln 5 trzeba uwzględnić n składników z

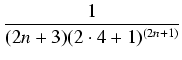
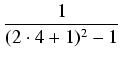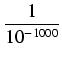
2$\displaystyle {\frac{{1}}{{(2n+3)(2 \cdot 4+1)^{(2n+1)}}}}$$\displaystyle {\frac{{1}}{{(2 \cdot 4+1)^2 - 1}}}$ < $\displaystyle {\frac{{1}}{{10^{-1000}}}}$

np. n = 600. Obliczenia wykonane za pomocą GP Pari dają:

ln 3 = 1.09861 22886 68109 69139 52452 36922 52570 46474 90557 82274 94517 34694 33363 74942 93218
60896 68736 15754 81373 20887 87970 02906 59578 65742 36800 42259 30519 82105 28018 70767 27741
06031 62769 18338 13671 79373 69884 43609 59903 74257 03167 95911 52114 55919 17750 67134 70549
40166 77558 02222 03170 25294 68975 60690 10652 15056 42868 13803 63173 73298 57778 23669 91654
79213 18181 49020 03010 38236 30122 24865 27481 98225 99109 74524 90896 45805 34670 08845 96508
57484 44119 01885 70876 47494 86707 96130 85829 41160 21661 21184 00140 98255 14391 94876 88936
79849 43022 55731 53532 96853 45295 25145 92138 76494 68593 25627 94416 55694 15782 72310 35516
88661 02118 46989 04399 43063 13825 52857 36466 88282 49881 36822 80063 41439 10786 89325 14564
37510 20445 16275 61934 97398 21169 41585 74053 53617 58900 97512 22337 97736 96968 77543 54795
13571 29821 77017 58124 21223 51405 81016 32724 65588 93724 95649 19185 24296 07966 84234 64706
93772 37252 65508 20320 78333 92805 58928 53146 87309 51326 06458 30918 43974 96822 23032 57654
67533 31182 30196 49275 25759 91322 17851 35339 02374 82964 33950 25460 74245 82493 46668 66121
88143 65265 65429 54276 76105 05477 79542 29339 73323 40

ln 5 = 1.60943 79124 34100 37460 07593 33226 18763 95256 01354 26851 77219 12647 89147 41789 87707
65776 46301 33878 09317 96107 99966 30302 17155 62899 72400 52293 24676 19963 36166 17463 70572
75521 79637 49718 32456 53492 85620 23415 25057 27015 51936 00879 77738 97256 88193 54071 27661
54731 22180 95279 48521 29282 13580 59722 56767 22852 87240 46158 94481 78364 67132 86739 98424
63775 95931 89423 84393 43534 51050 97505 44541 94740 50136 59870 87867 38321 31305 72972 04065
94853 83838 72366 27538 76545 56271 81615 11659 93091 52432 07364 91167 78639 00675 87258 57787
66391 58383 68239 50425 48795 62394 84031 00198 26971 17490 99374 14984 80957 62101 69110 14378
86240 33543 21512 72312 57345 88461 55978 72919 80886 57068 40200 66599 84447 26999 73217 68118
65176 01220 20297 84081 09019 64752 66997 65068 92065 89789 13381 57171 62072 27774 55977 05343
20387 78749 68293 75361 13380 09467 64048 33028 50021 74774 87970 80071 43465 61635 98970 41258
90133 76415 24017 00588 85987 34948 48778 79710 54314 17832 02014 53062 09061 57887 90671 59812
51674 99041 43417 21220 36944 70009 26855 93759 78549 21189 61786 43287 58768 48322 05835 59619
96791 31669 65093 23388 53158 53989 82370 98543 14631 10

ln 5 / ln 3 = 1.46497 35207 17927 16719 70404 07678 64039 63079 32366 66604 96890 52890 39479 54922 76191
02582 36555 93113 75952 94914 38497 38637 50382 77887 42660 37101 92682 85496 31995 32269 20487
96514 50611 55690 30210 66685 63896 30442 98927 53020 23869 77551 52938 00672 59928 94485 88766
40207 71832 51151 56581 41557 90827 91206 50489 79108 12691 41209 60417 49633 48383 81434 49803
16482 27549 45995 42996 81007 78174 37246 14062 50179 26983 62235 76045 55623 27002 26734 81574
87501 31182 30379 92179 67717 04321 93269 36472 71285 86478 64863 80138 89473 29078 57417 57545
58801 44030 11737 93412 34618 19223 74531 38141 56216 54221 59277 01824 27364 60119 67246 69210
39648 91159 72299 71039 08742 76647 72642 99759 91464 42093 01219 97112 28578 38177 99474 12031
83023 32846 88853 08269 14379 90922 99943 56964 40740 11717 01722 81846 28131 40449 48576 52181
90785 96525 15443 71104 18220 14444 06236 22635 50651 55300 01303 72764 84538 86958 21290 34203
78813 75106 37685 04951 69991 60073 17048 19381 31420 74568 55347 31084 23643 52954 25658 81967
39751 69015 10173 51086 77899 27056 75339 27465 29079 44019 78685 23958 68122 99776 70517 34910
98437 75117 08629 60957 66893 57959 18275 64893 45786 60

next up previous
Next: Liczba e Up: Liczby rzeczywiste Previous: Pi-ematy, czyli jak zapamiętać
Pawel Gladki 2006-01-30