


Next: Jak obliczyć liczbę ?
Up: Liczby rzeczywiste
Previous: Kto wynalazł cyfrę zero?
Nieskończony ułamek dzięsietny 0,(9) jest (z definicji) sumą szeregu geometrycznego
o pierwszym wyrazie a = 9/10 i ilorazie q = 1/10, więc
Ten rezultat jest powszechnie znany od czasu, gdy w 1584 roku ułamki dziesiętne wprowadził w Europie
do użytku Simon Stevin (na świecie - od 1427, al-Kaszi). Rezultat powinien znać każdy absolwent
czwartej klasy szkoły podstawowej. Jeśli juz wiemy, co oznacza napis 0,(9), to umiemy wykonywać
działania z tą liczba i wartość 0,(9) można obliczyś sprytniej:
9 . 0,(9) = (10 - 1) . 0,(9) = 9,(9) - 0,(9) = 9
0,(9) = 9/9 = 1.
Oczywista równość 0,(9) = 1 - jednak i o dziwo - budzi wielkie namiętności i prowadzi do kłótni,
a im mniej ktoś wie i rozumie, tym kategoryczniej się wypowiada...
Aby poznać tajniki magicznej równości 0,(9) = 1 nie trzeba nawet skończyć szkoły podstawowej,
wystarczy zapoznać się z zawartością podręcznika do jej czwartej klasy. Jest tam rozważany właśnie
problem liczby, której zapisem jako ułamek dziesiętny jest 0,(9). Wygląda to jakoś tak:
gdyby 0,(9) było mniejsze od 1, to jaka byłaby między nimi różnica? Mniejsza niż między 1 i 0,9;
mniejsza niż między 1 a 0,99; mniejsza niż między 1 a 0,999 - słowem różnica jest mniejsza niż
każdy ułamek 0,000000...001 - dowolnie długi. Zatem różnica wynosi 0.
Oczywiście to, co opisujemy, to wyjaśnienie, które kiedyś występowało w podręcznikach do szkoły
podstawowej. Jeśli to wyjaśnienie zapisać ściśle, to okaże się, że zawiera ono opis dowodu,
że dla każdej liczby dodatniej 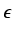 istnieje taka liczba naturalna N, że dla każdej
liczby naturalnej n > N zachodzi nierówność:
istnieje taka liczba naturalna N, że dla każdej
liczby naturalnej n > N zachodzi nierówność:
Jak dobrze wiemy, właśnie w taki sosób dowodzi się, że coś jest granicą jakiegoś ciągu
(nawet sum częściowych). I, naturalnie, nieskończoność zbioru liczb rzeczywistych nie ma
z tym nic wspólnego...
Załóżmy jednak przez chwilę, że 0,(9) nie równa się 1. Jeśli te liczby są różne,
to różnica między nimi musi być niezerowa. Oznaczmy ją literką r:
r = 1 - 0,(9)
i przyjrzyjmy się dokładniej tej różnicy. Zgodzimy się chyba z nierównościami:
0, 9 < 0,(9) < 1
- w takim razie badana różnica
r = 1 - 0,(9) jest mniejsza od
1 - 0, 9 = 0, 1. Jeszcze jeden krok:
0, 99 < 0,(9) < 1,
więc
r < 1 - 0, 99 = 0, 01, itd. To znaczy: jeśli wezmę pod uwagę skończony ułamek
dziesiętny 0, 9...9 z n dziewiątkami, to uzyskam w rezultacie nierówność
r < 1 - 0, 9...9 =
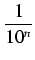
Co się okazuje? Liczba r jest dodatnia i mniejsza od każdej liczby postaci 1/(10n). Każdej!
Ale liczba mniejsza od 1/(10n) jest ułamkiem dziesiętnym postaci
0, 0...0... z n - 1 zerami
po przecinku. Gdy ktoś twierdzi, że r nie jest zerem, niech w takim razie poda, na którym miejscu
w rozwinięciu r na ułamek dziesiętny nieskończony jest pierwsza cyfra różna od zera.
Co można zaproponować? Miejsce milionowe? No to ja wezmę
n = 2000000 i okazuje się, że nie,
że po przecinku jest 1999999 zer. Miliardowe? To ja wezmę
n = 2000000001 i okazuje się, ze liczba
r ma po przecinku dwa miliardy zer. Ogólnie, jeśli zaproponuje się do sprawdzenia dowolne miejsce
dziesiętne m, to ja użyję n = 2m + 1 i widzę, że na miejscu m (i dłuuuugo dalej...) jest cyfra zero.
Dla dowolnego numeru m miejsca dziesiętnego cyfra w rozwinięciu liczby r na ułamek dziesiętny,
stojąca na tym miejscu jest równa zero. Czyli każda cyfra rozwinięcia dziesiętnego liczby r jest
równa zero. Bez względu na to, czy ktoś wszystkie dziewiątki wypisał czy nie, ja właśnie udowodniłem,
że każda cyfra jest zerem. Pozostaje zastanowić się, ile to jest r = 0,(0). Spróbujmy na przykład
dodać ją do jakiejś liczby...
Fakt, że ktoś gdzieś nie zdążył wypisać nieskończenie wielu dziewiątek w zapisie ułamka 0,(9)
nie ma wpływu na wartość liczby 0,(9) ani na równość 0,(9) = 1 - dokładnie na tej samej zasadzie,
jak fakt, że ktoś gdzieś nie zdążył napisać do końca cyfry 2 nie powoduje, ze 2 < 1 + 1.
I na tej samej zasadzie jak to, że zmazanie napisu "5" z tablicy nie spowoduje, że liczba 5 przestanie
istnieć, nie spowoduje, że wszyscy ludzie będą mieli po cztery palce.



Next: Jak obliczyć liczbę ?
Up: Liczby rzeczywiste
Previous: Kto wynalazł cyfrę zero?
Pawel Gladki
2006-01-30
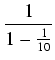 =
= ![]() istnieje taka liczba naturalna N, że dla każdej
liczby naturalnej n > N zachodzi nierówność:
istnieje taka liczba naturalna N, że dla każdej
liczby naturalnej n > N zachodzi nierówność: