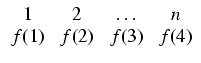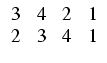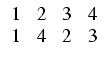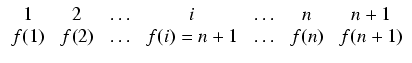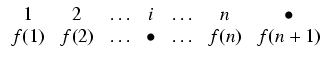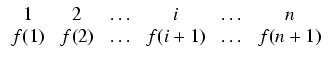Next: Wariacje bez powtórzeń
Up: Elementy kombinatoryki
Previous: Kombinacje
Zbiór Sn wszystkich wzajemnie jednoznacznych funkcji odwzorowujących zbiór n-elementowy na siebie.
Wzajemnie jednoznaczne odwzorowanie
f : X 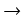 X nazywamy permutacją zbioru X.
Jeśli
X = {1, 2,..., n}, to permutacja f odpowiada sposobowi ustawienia jego elementów
w ciąg (bez powtórzeń)
(f (1), f (2),..., f (n)). Odwrotnie, każde takie ustawienie w ciąg
określa wzajemnie jednoznaczną funkcję f: f (x) to jest x-ty wyraz ciągu. Na przykład ciąg
(1, 2,..., n) w naturalnej kolejności odpowiada funkcji tożsamościowej f (x) = x.
Często wygodnie jest zapisywać permutacje f za pomocą tabelki funkcji f:
X nazywamy permutacją zbioru X.
Jeśli
X = {1, 2,..., n}, to permutacja f odpowiada sposobowi ustawienia jego elementów
w ciąg (bez powtórzeń)
(f (1), f (2),..., f (n)). Odwrotnie, każde takie ustawienie w ciąg
określa wzajemnie jednoznaczną funkcję f: f (x) to jest x-ty wyraz ciągu. Na przykład ciąg
(1, 2,..., n) w naturalnej kolejności odpowiada funkcji tożsamościowej f (x) = x.
Często wygodnie jest zapisywać permutacje f za pomocą tabelki funkcji f:
Jeśli górny wiersz tabelki jest w naturalnej kolejności, to dolny jest ciągiem, odpowiadąjcym
permutacji f. Tabelka ma tę przewagę nad ciągiem, że zmiana kolejności wypisywania elementów
nie przeszkadza w odczytaniu permutacji - odpowiada przestawieniu kolumn, które można z powrotem
uporządkowac:
Liczba | Sn| elementów zbioru Sn permutacji zbioru n-elementowego wyraża się wzorem:
| Sn| = n!.
Rzeczywiście, zbiór S0 ma jeden element (ciąg pusty, majacy 0 wyrazów) i 0! = 1;
zbiór S1 ma jeden element (ciąg jednowyrazowy) i 1! = 1. Załóżmy, że wzór na liczbę permutacji
jest prawdziwy dla pewnej liczby naturalnej n. Wyróżnijmy (i nazwijmy (n + 1)-szym) jeden element
zbioru (n + 1)-elementowego; pozostałe elementy tworzą zbiór n-elementowy. Każda permutacja zbioru
(n + 1)-elementowego powstaje z jednoznacznie określonej permutacji zbioru n-elementowego,
którą znajdujemy wykreślajac z tabelki (albo ciągu) (n + 1)-szy element i "dosuwając w lewo"
elementy dolnego wiersza tak, żeby nie było w nim pustego miejsca:
Zatem jest n! możliwosci utworzenia ciągu bez (n + 1)-szego elementu. Odtworzyć permutację (ciąg)
z ciągu bez (n + 1)-szego elementu można dopisując (n + 1)-szy element, przy czym można to zrobić
na n + 1 sposobów: (n + 1)-szy element można dopisać na początku (jako f (1)), przed drugim
(jako f (2)), ..., przed n-tym (jako f (n)) albo na końcu (jako f (n + 1)). Łącznie liczba
permutacji zbioru (n + 1)-elementowego jest równa
| Sn+1| = (n + 1) . | Sn| = (n + 1)n! = (n + 1)!
i wzór na liczbę permutacji jest prawdziwy dla wszystkich liczb naturalnych n na zasadzie indukcji
matematycznej.
Uwaga: Permutacje jednego zbioru można ze sobą składać (złożenie funkcji) i obliczać permutację
odwrotną (funkcja odwrotna). Łatwo to robić praktycznie za pomocą tabelek. W ten sposób zbiór
Sn z działaniem składania okazuje się grupą, zwaną grupą symetryczną.



Next: Wariacje bez powtórzeń
Up: Elementy kombinatoryki
Previous: Kombinacje
Pawel Gladki
2006-01-30
![]() X nazywamy permutacją zbioru X.
Jeśli
X = {1, 2,..., n}, to permutacja f odpowiada sposobowi ustawienia jego elementów
w ciąg (bez powtórzeń)
(f (1), f (2),..., f (n)). Odwrotnie, każde takie ustawienie w ciąg
określa wzajemnie jednoznaczną funkcję f: f (x) to jest x-ty wyraz ciągu. Na przykład ciąg
(1, 2,..., n) w naturalnej kolejności odpowiada funkcji tożsamościowej f (x) = x.
Często wygodnie jest zapisywać permutacje f za pomocą tabelki funkcji f:
X nazywamy permutacją zbioru X.
Jeśli
X = {1, 2,..., n}, to permutacja f odpowiada sposobowi ustawienia jego elementów
w ciąg (bez powtórzeń)
(f (1), f (2),..., f (n)). Odwrotnie, każde takie ustawienie w ciąg
określa wzajemnie jednoznaczną funkcję f: f (x) to jest x-ty wyraz ciągu. Na przykład ciąg
(1, 2,..., n) w naturalnej kolejności odpowiada funkcji tożsamościowej f (x) = x.
Często wygodnie jest zapisywać permutacje f za pomocą tabelki funkcji f: