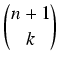Next: Permutacje
Up: Elementy kombinatoryki
Previous: Elementy kombinatoryki
Zbiór k-elementowych podzbiorów zbioru n-elementowego. Liczba jego elementów, czyli liczba
k-elementowych podzbiorów zbioru n-elementowego (zwanych kombinacjami n po k) oznaczana jest
symbolem Cnk i wyraża się wzorem:
W szczególności dla k > n liczba kombinacji Cnk jest równa 0. Ważne jest, że zliczamy
podzbiory, czyli kolejność elementów w zliczanych obiektach jest nieistotna.
Rzeczywiście, jeśli n = 0 lub n = 1 to łatwo sprawdzić, ze liczby:
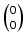 = 1,
= 1,
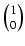 = 1 i
= 1 i
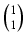 = 1 są równe liczbom C00 pustych podzbiorów zbioru pustego,
C10 pustych podzbiorów zbioru jednoelementowego i C11 jednoelementowych podzbiorów zbioru
jednoelementowego. Załóżmy, ze wzór na liczbę kombinacji jest słuszny dla pewnej liczby n
i wszystkich
k
= 1 są równe liczbom C00 pustych podzbiorów zbioru pustego,
C10 pustych podzbiorów zbioru jednoelementowego i C11 jednoelementowych podzbiorów zbioru
jednoelementowego. Załóżmy, ze wzór na liczbę kombinacji jest słuszny dla pewnej liczby n
i wszystkich
k 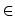 {0, 1,..., n}. Policzymy podzbiory k-elementowe zbioru, mającego n + 1
elementów. Wyróżnijmy w tym zbiorze jeden element - nazwijmy go (n + 1)-szym elementem. Pozostałe
elementy tworzą zbiór n-elementowy. Zbiór wszystkich k-elementowych podzbiorów można teraz
podzielić na dwa rozłączne podzbiory:
{0, 1,..., n}. Policzymy podzbiory k-elementowe zbioru, mającego n + 1
elementów. Wyróżnijmy w tym zbiorze jeden element - nazwijmy go (n + 1)-szym elementem. Pozostałe
elementy tworzą zbiór n-elementowy. Zbiór wszystkich k-elementowych podzbiorów można teraz
podzielić na dwa rozłączne podzbiory:
- pierwszy składa się z tych podzbiorów k-elementowych, do których (n + 1)-szy element nie należy;
są więc one k-elementowymi podzbiorami zbioru n-elementowego i jest ich
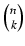
- drugi składa się z tych podzbiorów k-elementowych, do których (n + 1)-szy element należy;
każdy z nich powstaje z jednoznacznie określonego (k - 1)-elementowego podzbioru zbioru n-elementowego
przez dołączenie (n + 1)-szego elementu; zatem takich podzbiorów jest tyle, co (k - 1)-elementowych
podzbiorów zbioru n-elementowego - jest ich
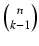
Łącznie zbiór kombinacji n + 1 po k ma
elementów. Na zasadzie indukcji matematycznej wzór na liczbę kombinacji jest prawdziwy dla każdej
liczby naturalnej n.



Next: Permutacje
Up: Elementy kombinatoryki
Previous: Elementy kombinatoryki
Pawel Gladki
2006-01-30
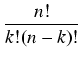 =
= 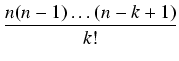
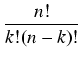 =
= 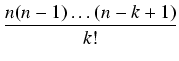
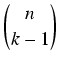 =
=