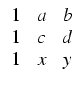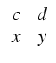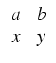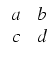Wzajemne położenie punktów i prostych

Jak wiadomo, prosta dzieli płaszczyznę na dwie półpłaszczyzny, które nazywamy (czasem) stronami. Jeśli równanie prostej zapisać w postaci:

Ax + By + C = 0

(równanie ogólne prostej na płaszczyźnie), to ten podział sprowadza się do rachunku:

• jedna strona składa się z tych punktów (x, y), dla których Ax + By + C < 0,
• druga strona składa się z tych punktów (x, y), dla których Ax + By + C > 0,
• przedzielająca je prosta - z tych punktów (x, y), dla których Ax + By + C = 0.

Oczywiście to, która strona jest "ujemna", a która "dodatnia", zależy od wyboru równania ogólnego prostej: x - y = 0 i y - x = 0 to dwa równania ogólne tej samej prostej y = x, i strona "ujemna" dla jednego równania jest "dodatnia" dla drugiego równania:

x - y > 0 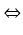$$\Leftrightarrow$$ y - x < 0.

Stronę prostej można wybrać, podając punkt, który do niej należy, np. strona prostej y = x do której należy punkt (1, 0) jest "dodatnia" dla równania x - y = 0 i "ujemna" dla równania y - x = 0.

Dwa punkty P = (x₁, y₁) oraz P = (x₂, y₂)

• leżą po tej samej stronie prostej Ax + By + C = 0 gdy wyrażenie
  (Ax₁ + By₁ + C)(Ax₂ + By₂ + C)
  jest dodatnie,
• leżą po przeciwnych stronach prostej Ax + By + C = 0 gdy wyrażenie
  (Ax₁ + By₁ + C)(Ax₂ + By₂ + C)
  jest ujemne,
• gdy ten iloczyn jest zerem, to choć jeden z punktów leży na prostej.

Pólpłaszczyzny są ważne, bo każdy zbiór wypukły na płaszczyźnie jest częścią wspólną zawierających go półpłaszczyzn, a gdy zbiór jest wielokątem wystarczy skończona liczba półpłaszczyn - wyznaczonych przez boki wielokąta.

Warto pamiętać, że prosta przechodząca przez dwa różne punkty (a, b), (c, d ) ma równanie ogólne

$$\left\vert\vphantom{ \begin{array}{ccc} 1 & a & b \\ 1 & c & d \\ 1 & x & y \end{array} }\right.$$$$\begin{array}{ccc} 1 & a & b \\ 1 & c & d \\ 1 & x & y \end{array}$$$$\left.\vphantom{ \begin{array}{ccc} 1 & a & b \\ 1 & c & d \\ 1 & x & y \end{array} }\right\vert$$ = 0

czyli:

$$\left\vert\vphantom{ \begin{array}{cc} c & d \\ x & y \end{array} }\right.$$$$\begin{array}{cc} c & d \\ x & y \end{array}$$$$\left.\vphantom{ \begin{array}{cc} c & d \\ x & y \end{array} }\right\vert$$ - $$\left\vert\vphantom{ \begin{array}{cc} a & b \\ x & y \end{array} }\right.$$$$\begin{array}{cc} a & b \\ x & y \end{array}$$$$\left.\vphantom{ \begin{array}{cc} a & b \\ x & y \end{array} }\right\vert$$ + $$\left\vert\vphantom{ \begin{array}{cc} a & b \\ c & d \end{array} }\right.$$$$\begin{array}{cc} a & b \\ c & d \end{array}$$$$\left.\vphantom{ \begin{array}{cc} a & b \\ c & d \end{array} }\right\vert$$ = 0

czyli:

(b - d )x + (c - a)y + (ad - bc) = 0.