Poznane przez was wiadomości o interpretacji graficznej pochodnej funkcji w punkcie można stosować w rozwiązywaniu różnych problemów i zadań matematycznych.

Strony, które prezentujemy z pewnością nie wyczerpują tego tematu, a jedynie wprowadzają i sygnalizują te miejsca w matematyce, gdzie wiedzę o graficznej interpretacji pochodnej można wykorzystać.

I oto jeszcze jedno zastosowanie:

 Zastanów się w jaki sposób obliczyć kąt jaki tworzą  dwie przecinające się  krzywe, będące wykresami pewnych funkcji?

 

 

Na początku  musimy zdefiniować kąt między krzywymi:

Kąt jaki tworzą styczne do krzywych w punkcie ich przecięcia to kąt pomiędzy tymi krzywymi.

 

  Wobec tego, aby wyznaczyć kąt między krzywymi należy wykonać następujące czynności:

 (jeśli chcesz zobaczyć na przykładzie  jak wykonać daną czynność kliknij na numer)

1. Wyznaczyć punkt przecięcia krzywych

 

2.Wyznaczyć współczynniki kierunkowe stycznych do krzywych, tzn. obliczyć pochodne funkcji, którymi opisane są krzywe, w wyznaczonym wcześniej punkcie.

 

3.Wyznaczyć kąt między stycznymi korzystając z interpretacji geometrycznej współczynnika kierunkowego prostej.

 

Prezentujemy przykład rozwiązania zadania tego typu:

 

Zadanie: Wyznacz kąt pod jakim przecinają się wykresy funkcji: y=sin x, y= cos x

 

Rozwiązanie:

 

Ad1. Korzystając z wykresów funkcji trygonometrycznych  wyznaczamy punkty przecięcia się krzywych.

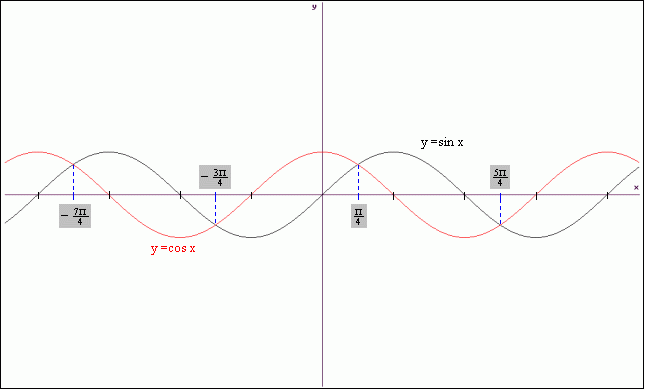
Ogólnie rozwiązanie równania : sin x=cos x można zapisać następująco:

 

                        ,     , gdzie  

 

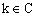
Korzystając z okresowości funkcji sin x i cos x wnioskujemy, że wystarczy rozważyć tylko rozwiązania z przedziału <0 , 2p >, ponieważ w pozostałych punktach sytuacja się powtarza.

 

Ad.2 Zanim wyznaczymy współczynniki kierunkowe stycznych w punktach: ,

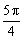
przyjrzyjmy się uważnie rysunkowi:

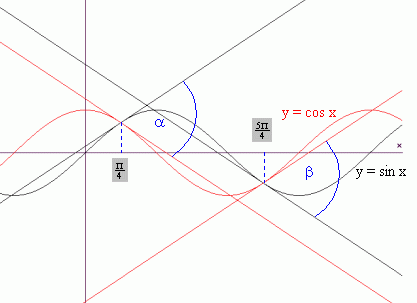
Styczna do sinusoidy w punkcie   jest równoległa do stycznej do cosinusoidy w  punkcie  , i analogicznie równoległe są styczne do cosinusoidy w punkcie   i do sinusoidy w punkcie . Oznacza to, że kąty a i b są równe. Zatem wystarczy wyznaczyć współczynniki kierunkowe stycznych w punkcie .

Niech kąt d oznacza kąt między styczną do sinusoidy a osią x, zaś a kąt g kąt między styczną do cosinusoidy a osią x, w punkcie .

 

tg d=sin'()=cos()=

tg g=cos'()=-sin()=-

Ad.3  Szukany kąt ostry między krzywymi jest równy różnicy d - g  .

 

tg (d - g)= =

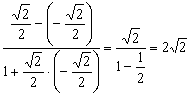
d - g ~70^o30'