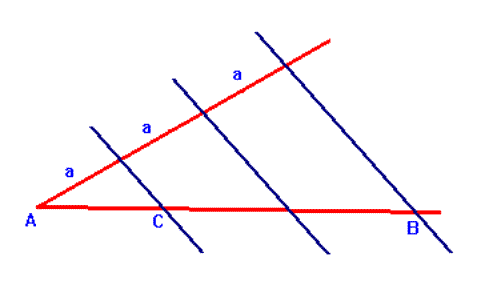
 |
Na rysunku obok trzy proste przecinające ramiona kąta są równoległe. Z twierdzenia Talesa wynika, że |
Konstrukcja: Podział danego odcinka na trzy równe części.
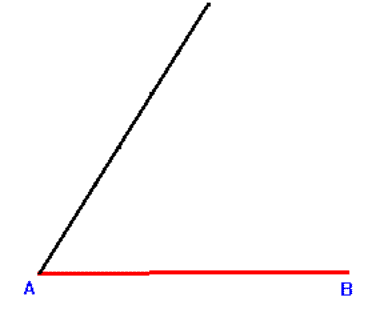 |
1. Rysujemy dowolną półprostą o początku w punkcie A, nachyloną do odcinka AB pod kątem ostrym. | 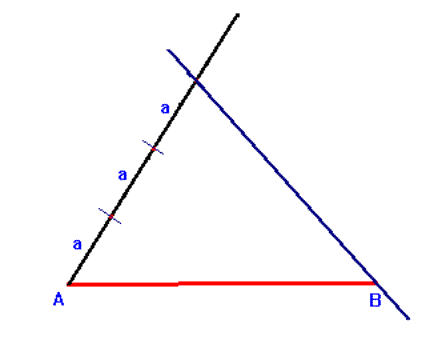 |
2. Na półprostej odkładamy kolejno trzy odcinki jednakowej długości. Prowadzimy prostą przez punkt B i koniec ostatniego odcinka. |
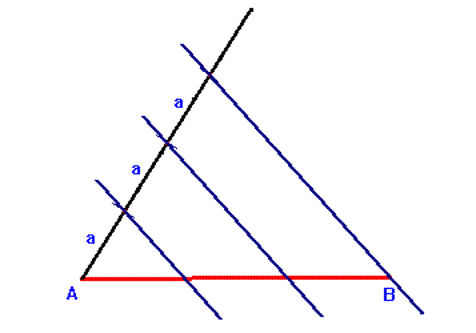 |
3. Kreślimy proste równoległe do narysowanej prostej, przechodzące przez pozostałe dwa końce odkładanych odcinków. Dzielą one odcinek AB na trzy równe części. |
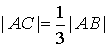 .
.

