TWIERDZENIE TALESA

Legenda głosi, że starożytny mędrzec Tales z Miletu potrafił za pomocą cienia wyznaczać wysokości piramid i drzew.

Przyjrzyj się rysunkowi i uzupełnij luki !

Cień drzewa jest razy dłuższy od cienia człowieka.
Zatem drzewo jest razy wyższe od człowieka.
Drzewo ma metra wysokości.

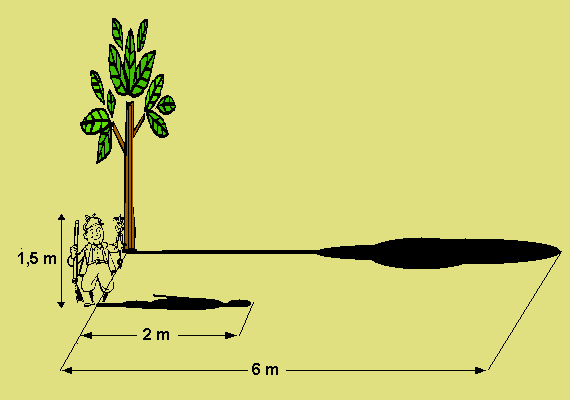
Tales przy swoich pomiarach korzystał z faktu, że długości cieni są wprost proporcjonalne
(w skrócie mówimy, że są proporcjonalne) do wysokości przedmiotów rzucających te cienie.

Teraz drzewo, człowieka i ich cienie zastąpimy odcinkami.




Przyjrzyj się rysunkowi i uzupełnij luki !

Na tym rysunku proste k i t są równoległe.
Odcinek 7,2 m jest razy dłuższy od odcinka 2,4 m.
Zatem odcinek x m jest razy dłuższy od odcinka 1,6 m.

Prawdziwa jest równość:

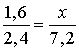
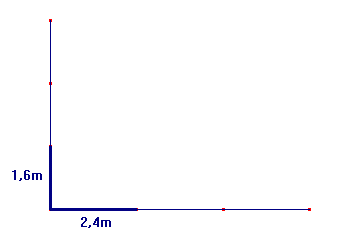
to znaczy, że odcinki 1.6m i 2,4m są proporcjonalne do odcinków xm i 7,2m

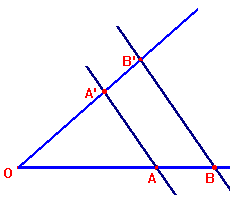Ogólną własność dotyczącą tego problemu sformuował Tales z Miletu.

Twierdzenie Talesa
Jeżeli ramiona kąta przetniemy prostymi równoległymi to odcinki powstałe na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków powstałych na drugim ramieniu kąta.


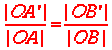
Uwaga: Zakładamy, że kąt ma miarę mniejszą niż 180 stopni.

Jeżeli w proporcji:

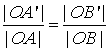
przestawimy wyrazy skrajne lub wyrazy środkowe, to otrzymamy proporcje:

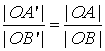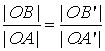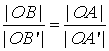a to oznacza, że odcinki jednej prostej są proporcjonalne do odpowiednich odcinków drugiej prostej.

ĆWICZENIE:

Znajdź pary odcinków proporcjonalnych.

AA' || BB' || CC'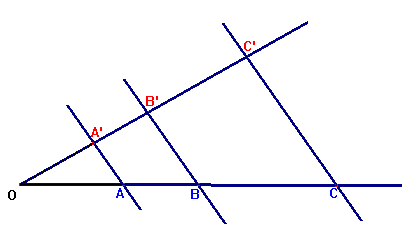


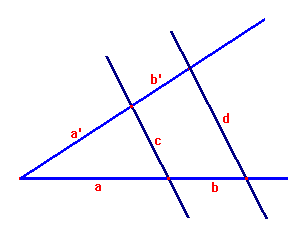
Z twierdzenia Talesa wynika wiele proporcji, które często są wykorzystywane przy rozwiązywaniu zadań. Oto niektóre z tych proporcji:
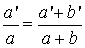
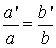
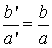
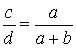
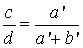