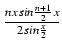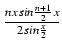W tym ustępie podajemy około 30 tożsamości trygonometrycznych, których biegłe opanowanie pamięciowe,
wraz z dowodami, uważamy za niezbędne. Tożsamości te dzielą się na kilka grup. Poszczególne tożsamości
mają nazwy, których brzmienie jest niekiedy podobne, np. "sinus sumy" i "suma sinusów". Ucząc się
ich, należy zwracać uwagę na kolejność działań, gdyż takie wyrażenia jak
sin(![]() +
+ ![]() )
i
sin
)
i
sin![]() + sin
+ sin![]() są na ogół nierówne.
są na ogół nierówne.
Funkcje sumy kątów.
Twierdzenie: Funkcje trygonometryczne sumy dwóch kątów wyrażają się następującymi wzorami:
Pierwsze dwa wzory są prawdziwe dla wszelkich ![]() i
i ![]() . Wzór na tangens sumy jest prawdziwy dla wszystkich
. Wzór na tangens sumy jest prawdziwy dla wszystkich
![]() ,
,![]() ,
oprócz tych, dla których tg
,
oprócz tych, dla których tg![]() , tg
, tg![]() lub
tg(
lub
tg(![]() +
+ ![]() ) jest nieokreślony.
) jest nieokreślony.
Dowód: Rozważymy następujące przypadki:
Przypadek, gdy jeden z kątów
![]() ,
,![]() jest zerowy lub prosty. Wówczas prawdziwośc wzorów
jest oczywista albo wynika bezpośrednio ze wzorów redukcyjnych.
jest zerowy lub prosty. Wówczas prawdziwośc wzorów
jest oczywista albo wynika bezpośrednio ze wzorów redukcyjnych.
Przypadek, gdy ![]() i
i ![]() należą do I ćwiartki. Wówczas
należą do I ćwiartki. Wówczas
![]() +
+ ![]() należy do I lub
II ćwiartki:
należy do I lub
II ćwiartki:
![\includegraphics[width=12cm]{105-1.eps}](img958.gif)
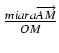 . Ponieważ
. Ponieważ
| sin( |
= | 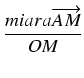 = = 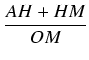 = = |
|
| = | 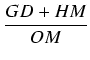 = = |
||
| = |
W dowodzie wzoru na cosinus sumy korzystamy z tego, że
![]() =
= ![]() +
+ ![]() =
= ![]() -
- ![]() .
Wektory
.
Wektory
![]() ,
,
![]() są skierowane zgodnie z osią OX, więc
miara
są skierowane zgodnie z osią OX, więc
miara![]() = OG - AG
= OG - AG
| cos( |
= | 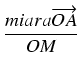 = = 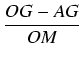 = = |
|
| = | |||
| = |
Dzięki związkom wymienionym powyżej, otrzymane wyrażenie równa się
cos![]() cos
cos![]() - sin
- sin![]() sin
sin![]() ,
co dowodzi prawdziwości wzoru na cosinus sumy.
,
co dowodzi prawdziwości wzoru na cosinus sumy.
Przypadek, gdy ![]() lub
lub ![]() nie należą do I ćwiartki. Przypadek taki sprowadza się
do poprzedniego za pomocą wzorów redukcyjnych.
nie należą do I ćwiartki. Przypadek taki sprowadza się
do poprzedniego za pomocą wzorów redukcyjnych.
Wzór na tangens sumy wynika bezpośrednio ze wzorów na sinus i cosinus sumy:
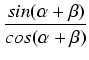 =
= 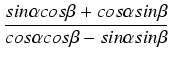 .
.
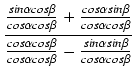 =
= 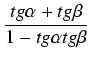
Funkcje różnicy kątów.
Zastępując we wzorach na funkcje sumy kątów kąt ![]() kątem -
kątem - ![]() i stosując wzory redukcyjne, otrzymujemy:
i stosując wzory redukcyjne, otrzymujemy:
Funkcje kąta podwójnego.
Zastępując we wzorach na funkcje sumy kątów kąt ![]() kątem
kątem ![]() otrzymujemy:
otrzymujemy:
Korzystając z "jedynki trygonometrycznej" można cosinus kąta podwójnego wyrazić w postaciach:
Funkcje połowy kąta.
Jeśli we wzorach na funkcje kąta podwójnego zastąpimy kąt ![]() kątem
kątem
![]() , to otrzymamy wzory:
, to otrzymamy wzory:
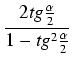
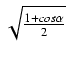
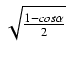
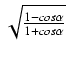
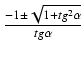
Wadą powyższych wzorów jest dwoistość znaku i postać niewymierna (pierwiastek). Wolne od tych wad są wzory:
Dowód: Udowodnimy pierwszy ze wzorów - drugi dowodzi się analogicznie:
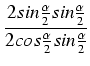 =
= 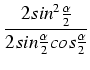 =
= 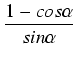 .
.
Sumy i różnice funkcji trygonometrycznych.
Twierdzenie: Sumy i różnice funkcji trygonometrycznych wyrażają się wzorami:
Dowód: Udowodnimy tylko pierwszy zw wzorów - pozostałe dowodzi się analogicznie. Do dwóch danych liczb
![]() ,
, ![]() można zawsze dobrać takie dwie liczby x, y, że
można zawsze dobrać takie dwie liczby x, y, że
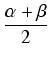 , y =
, y = 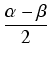 .
.
| sin |
= | sin(x + y) + sin(x - y) = | |
| = | sinxcosy + cosxsiny + sinxcosy - cosxsiny = | ||
| = | 2sinxcosy = 2sin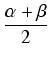 cos cos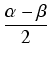 . . |
Pozostałe tożsamości.
Korzystając z podstawowych tożsamości wypowadzonych powyżej (oraz - w czterech ostatnich przypadkach - także z zasady indukcji matematycznej) z łatwością dowodzi się następujących, pożytecznych wzorów: