Next: Wykresy funkcji trygonometrycznych Up: Funkcje trygonometryczne kąta skierowanego Previous: Związki między funkcjami trygonometrycznymi

Wzory redukcyjne

Kąty $\alpha$ , 180^o - $\alpha$ , 180^o + $\alpha$ , - $\alpha$ . W tablicach podaje się wartości funkcji trygonometrycznych jedynie dla kątów I ćwiartki. W pozostałych ćwiartkach bowiem występują te same wartości, jedynie ich kolejność może być zmieniona lub znak. Widać to na kole trygonometrycznym:

$\includegraphics[width=12cm]{102-1.eps}$

Obierzmy promień koła r = 1, wówczas rzędna jest równa sinusowi, a odcięta - cosinusowi danego kąta.

Weźmy pod uwagę cztery kąty:

$\displaystyle \alpha$ , 180^o - $\displaystyle \alpha$ , 18 + $\displaystyle \alpha$ , - $\displaystyle \alpha$

i odpowiadające tym kątom cztery punkty okręgu

M, M₁, M₂, M₃.

Jeśli kąt $\alpha$ należy do I ćwiartki, to kąty 180^o - $\alpha$ , 180^o + $\alpha$ , - $\alpha$ należą odpowiednio do ćwiartek II, III i IV. Punkty powyższe leżą symetrycznie, a mianowicie:

punkt M₁ jest symetryczny do punktu M względem osi rzędnych,
punkt M₂ jest symetryczny do punktu M względem początku układu,
punkt M₃ jest symetryczny do punktu M względem osi odciętych.

Dzięki tej symetrii, łatwo wyznaczyć współrzędne punktów M₁, M₂, M₃, jeśli znane są współrzędne M. Oznaczmy współrzędne punktu M literami x, y; wówczas odczytujemy:

M(x, y), M₁(- x, y), M₂(- x, - y), M₃(x, - y).

Rzędne tych punktów są sinusami, a odcięte - cosinusami kątów. Mamy więc dla tych kątów następujące wartości sinusa i cosinusa:

	$\displaystyle \alpha$	180^o - $\displaystyle \alpha$	180^o + $\displaystyle \alpha$	- $\displaystyle \alpha$
sin	y	y	- y	- y
cos	x	- x	- x	x

Porównując ze sobą te wartości, stwierdzamy, że sinus przyjmuje dla kątów $\alpha$ i 180^o - $\alpha$ tę samą wartość

sin(180^o - $\displaystyle \alpha$ ) = sin $\displaystyle \alpha$

natomiast dla kątów $\alpha$ i - $\alpha$ sinus przyjmuje wartości przeciwne

sin(- $\displaystyle \alpha$ ) = - sin $\displaystyle \alpha$ .

W podobny sposób odczytujemy dalsze związki. Zestawiamy je w poniższej tabeli:

180^o - $\displaystyle \alpha$	180^o + $\displaystyle \alpha$	- $\displaystyle \alpha$
sin(180^o - $\displaystyle \alpha$ ) = sin $\displaystyle \alpha$	sin(180^o + $\displaystyle \alpha$ ) = - sin $\displaystyle \alpha$	sin(- $\displaystyle \alpha$ ) = - sin $\displaystyle \alpha$
cos(180^o - $\displaystyle \alpha$ ) = - cos $\displaystyle \alpha$	cos(180^o + $\displaystyle \alpha$ ) = - cos $\displaystyle \alpha$	cos(- $\displaystyle \alpha$ ) = cos $\displaystyle \alpha$
tg(180^o - $\displaystyle \alpha$ ) = - tg $\displaystyle \alpha$	tg(180^o + $\displaystyle \alpha$ ) = tg $\displaystyle \alpha$	tg(- $\displaystyle \alpha$ ) = - tg $\displaystyle \alpha$
ctg(180^o - $\displaystyle \alpha$ ) = - ctg $\displaystyle \alpha$	ctg(180^o + $\displaystyle \alpha$ ) = ctg $\displaystyle \alpha$	ctg(- $\displaystyle \alpha$ ) = - ctg $\displaystyle \alpha$

Wzorów redukcyjnych jest dość dużo. Istotne jest nie tyle wyuczenie się ich na pamięć, co umiejętność wyprowadzania tych wzorów. To zaś polega na właściwym odczytywaniu prostych rysunków. Pokazujemy to poniżej na paru przykładach.

Wzory dla kąta 180^o - $\alpha$ . Rozważmy kąty $\alpha$ i 180^o - $\alpha$ w położeniu standardowym:

$\includegraphics[width=12cm]{102-2.eps}$

Z kątem 180^o - $\alpha$ można skojarzyć wyobrażenie obrotu złożonego z obrotu o kąt 180^o i obrotu o kąt - $\alpha$ . Oba kąty kreślimy w jednym układzie, zataczamy okrąg i na otrzymanym w ten sposób kole trygonometrycznym odczytujemy rzędne i odcięte punktów M i M':

$\includegraphics[width=12cm]{102-3.eps}$

Rzędne są jednakowe, natomiast odcięte są liczbami przeciwnymi. Stąd odczytujemy, że jest:

sin(180^o - $\displaystyle \alpha$ ) = sin $\displaystyle \alpha$ , cos(180^o - $\displaystyle \alpha$ ) = - cos $\displaystyle \alpha$ .

Dzieląc pierwszą z tych równości przez drugą otrzymujemy wzór:

tg(180^o - $\displaystyle \alpha$ ) = - tg $\displaystyle \alpha$ .

Wzory dla kąta 180^o + $\alpha$ wyprowadzamy za pomocą następującego rysunku:

$\includegraphics[width=12cm]{102-4.eps}$

Wzory dla kąta - $\alpha$ wyprowadzamy korzystając z poniższej ilustracji:

$\includegraphics[width=12cm]{102-5.eps}$

Kąty $\alpha$ i 90^o - $\alpha$ . Rozważmy kąty $\alpha$ i 90^o - $\alpha$ w położeniu standardowym (rysunek a)):

$\includegraphics[width=12cm]{102-6.eps}$

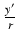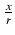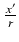Końcowe ramiona tych kątów l i l' są wzajemnie symetryczne względem prostej dwusiecznej kąta XOY. Obierzmy punkty M(x, y) i M'(x', y') leżące odpowiednio na l i l' tak, aby OM = OM' = r > 0. Współrzędne tych punktów spełniają związki x' = y, y' = x (rysunek b)). 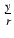Stąd sin(90^o - $\alpha$ ) = ${\frac{{y'}}{{r}}}$ = ${\frac{{x}}{{r}}}$ = cos $\alpha$ oraz cos(90^o - $\alpha$ ) = ${\frac{{x'}}{{r}}}$ = ${\frac{{y}}{{r}}}$ = sin $\alpha$ . Ponieważ symetria półprostych l i l' zachdzi dla dowolnego $\alpha$ , więc dla dowolnego $\alpha$ mamy związki

sin(90^o - $\displaystyle \alpha$ ) = cos $\displaystyle \alpha$ , cos(90^o - $\displaystyle \alpha$ ) = sin $\displaystyle \alpha$ .

Związki te nazywamy wzorami redukcyjnymi dla kąta 90^o - $\alpha$ . Odpowiedni wzór dla tangensa i cotangensa otrzymamy, dzieląc przez siebie stronami powyższe równości:

tg(90^o - $\displaystyle \alpha$ ) = ctg $\displaystyle \alpha$ .

Kąty 90^o - $\alpha$ i 90^o + $\alpha$ . Rozważmy odpowiednie kąty w położeniu standardowym (rysunek a)):

$\includegraphics[width=12cm]{102-7.eps}$

Końcowe ramiona tych kątów są półprostymi l' i l'' położonymi symetrycznie względem osi rzędnych. Współrzędne punktów M' i M'' leżących na tych półprostych tak, aby OM' = OM'' = r > 0 (rysunek b)) spełniają związki x'' = - x', y'' = y'. Stąd:

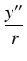
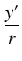
sin(90^o + $\displaystyle \alpha$ ) = $\displaystyle {\frac{{y''}}{{r}}}$ = $\displaystyle {\frac{{y'}}{{r}}}$ = sin(90^o - $\displaystyle \alpha$ ) = cos $\displaystyle \alpha$ ,

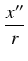
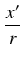
cos(90^o + $\displaystyle \alpha$ ) = $\displaystyle {\frac{{x''}}{{r}}}$ = - $\displaystyle {\frac{{x'}}{{r}}}$ = - cos(90^o - $\displaystyle \alpha$ ) = - sin $\displaystyle \alpha$ .

W ten sposób wyprowadziliśmy wzory redukcyjne dla kąta 90^o + $\alpha$ :

sin(90^o + $\displaystyle \alpha$ ) = cos $\displaystyle \alpha$ , cos(90^o + $\displaystyle \alpha$ ) = - sin $\displaystyle \alpha$ .

Dzieląc stronami, otrzymujemy:

tg(90^o + $\displaystyle \alpha$ ) = - ctg $\displaystyle \alpha$ .

Podsumujmy otrzymane rezultaty w tabeli:

90^o - $\displaystyle \alpha$	90^o + $\displaystyle \alpha$
sin(90^o - $\displaystyle \alpha$ ) = cos $\displaystyle \alpha$	sin(90^o + $\displaystyle \alpha$ ) = cos $\displaystyle \alpha$
cos(90^o - $\displaystyle \alpha$ ) = sin $\displaystyle \alpha$	cos(90^o + $\displaystyle \alpha$ ) = - sin $\displaystyle \alpha$
tg(90^o - $\displaystyle \alpha$ ) = ctg $\displaystyle \alpha$	tg(90^o + $\displaystyle \alpha$ ) = - ctg $\displaystyle \alpha$
ctg(90^o - $\displaystyle \alpha$ ) = tg $\displaystyle \alpha$	ctg(90^o + $\displaystyle \alpha$ ) = - tg $\displaystyle \alpha$

Kąty 45^o - $\alpha$ i 45^o + $\alpha$ . Rozważmy odpowiednie kąty w położeniu standardowym:

$\includegraphics[width=12cm]{102-8.eps}$

Kąty te mają ramiona końcowe położone symetrycznie względem prostej dwusiecznej I i III ćwiartki, a punkty M, M' leżące na tych ramionach, OM = OM' = r > 0, mają współrzędne (x, y) i (x', y'), przy czym jest x' = y, y' = x. Stąd wynikają wzory redukcyjne:

sin(45^o + $\displaystyle \alpha$ ) = cos(45^o - $\displaystyle \alpha$ ),

cos(45^o + $\displaystyle \alpha$ ) = sin(45^o - $\displaystyle \alpha$ ),

tg(45^o + $\displaystyle \alpha$ ) = ctg(45^o - $\displaystyle \alpha$ ),

ctg(45^o + $\displaystyle \alpha$ ) = tg(45^o - $\displaystyle \alpha$ ).

Next: Wykresy funkcji trygonometrycznych Up: Funkcje trygonometryczne kąta skierowanego Previous: Związki między funkcjami trygonometrycznymi

Pawel Gladki 2006-01-30