


Next: Całki funkcji zawierających pierwiastek
Up: Rachunek całkowy
Previous: Całki funkcji trygonometrycznych
Jeżeli funkcja podcałkowa jest funkcją wymierną potęg zmiennej x o wykładnikach postaci
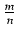 ,
gdzie m, n są liczbami naturalnymi względnie pierwszymi, to wykonujemy podstawienie:
,
gdzie m, n są liczbami naturalnymi względnie pierwszymi, to wykonujemy podstawienie:
x = tN
gdzie N jest wspólnym mianownikiem wszystkich ułamków postaci
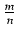 .
.
Przykład: Obliczyć całkę:

![$\displaystyle {\frac{{dx}}{{\sqrt{x} + \sqrt[3]{x}}}}$](img536.gif)
.
Funkcja podcałkowa jest funkcją wymierną potęg zmiennej x o wykładnikach
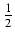 oraz
oraz
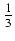 .
Wspólnym mianownikiem powyższych ułamków jest 6, wykonujemy więc podstawienie:
.
Wspólnym mianownikiem powyższych ułamków jest 6, wykonujemy więc podstawienie:
x = t6.
Stąd
dx = 6t5dt,
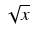 = t3,
= t3,
![$ \sqrt[3]{{x}}$](img538.gif) = t2 i otrzymujemy całkę:
= t2 i otrzymujemy całkę:

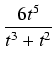 dt
dt,
którą dalej liczymy znanymi metodami liczenia całek z funkcji wymiernych.
Jeżeli funkcja podcałkowa jest funkcją wymierną zmiennej x oraz
- potęg dwumianu ax + b lub
- funkcji homograficznej
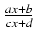 (gdzie
ad - bc
(gdzie
ad - bc 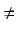 0)
0)
o wykładnikach postaci
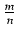 , gdzie m, n sa liczbami naturalnymi względnie pierwszymi,
to w pierwszym wypadku wykonujemy podstawienie
, gdzie m, n sa liczbami naturalnymi względnie pierwszymi,
to w pierwszym wypadku wykonujemy podstawienie
ax + b = tN
a w drugim przypadku:
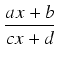
=
tN
gdzie N oznacza wspólny mianownik ułamków postaci
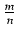 .
.
Przykład: Obliczyć całkę:

![$\displaystyle {\frac{{x \sqrt{2x - 10}}}{{2 - \sqrt[3]{2x - 10}}}}$](img542.gif)
.
Funkcja podcałkowa jest funkcją wymierną zmiennej x oraz potęg dwumianu 2x - 10 o wykładnikach
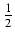 oraz
oraz
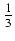 . Wspólnym mianownikiem powyższych ułamków jest 6, wykonujemy więc podstawienie:
. Wspólnym mianownikiem powyższych ułamków jest 6, wykonujemy więc podstawienie:
2x - 10 = t6.
Stąd
2dx = 6t5dt, czyli
dx = 3t5dt,
x = 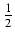 t6 + 5,
t6 + 5,
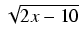 = t3,
= t3,
![$ \sqrt[3]{{2x - 10}}$](img544.gif) = t2 i otrzymujemy całkę:
= t2 i otrzymujemy całkę:

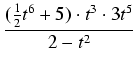 dt
dt
którą dalej liczymy znanymi metodami liczenia całek z funkcji wymiernych.
Przykład: Obliczyć całkę:
Funkcja podcałkowa jest funkcją wymierną zmiennej x oraz potęgi funkcji homograficznej
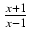 o wykładniku
o wykładniku
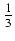 , wykonujemy więc podstawienie:
, wykonujemy więc podstawienie:
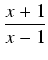
=
t3.
Stąd
x = 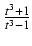 ,
dx =
,
dx = 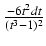 i otrzymujemy całkę:
którą (po uproszczeniu) liczmy dalej znanymi metodami.
i otrzymujemy całkę:
którą (po uproszczeniu) liczmy dalej znanymi metodami.
Ćwiczenia:
-

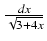 Odpowiedź:
Odpowiedź:
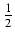
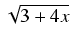 + C
+ C
-
 x
x![$ \sqrt[3]{{x-4}}$](img556.gif) dx Odpowiedź:
dx Odpowiedź:
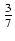 (x2 - x - 12)
(x2 - x - 12)![$ \sqrt[3]{{x-4}}$](img556.gif) + C
+ C
-

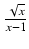 dx Odpowiedź:
2
dx Odpowiedź:
2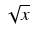 + ln|
+ ln|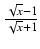 | + C
| + C
-

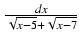 Odpowiedź:
Odpowiedź:
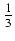 ((x - 5)
((x - 5)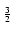 - (x - 7)
- (x - 7)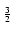 ) + C
) + C
-

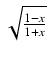 .
. 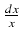 Odpowiedź:
ln| 1 -
Odpowiedź:
ln| 1 - 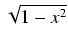 | - ln| x| - arcsinx + C
| - ln| x| - arcsinx + C



Next: Całki funkcji zawierających pierwiastek
Up: Rachunek całkowy
Previous: Całki funkcji trygonometrycznych
Pawel Gladki
2006-01-30
![]() ,
gdzie m, n są liczbami naturalnymi względnie pierwszymi, to wykonujemy podstawienie:
,
gdzie m, n są liczbami naturalnymi względnie pierwszymi, to wykonujemy podstawienie:
![$\displaystyle {\frac{{dx}}{{\sqrt{x} + \sqrt[3]{x}}}}$](img536.gif) .
.
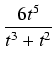 dt,
dt,
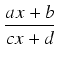 = tN
= tN
![$\displaystyle {\frac{{x \sqrt{2x - 10}}}{{2 - \sqrt[3]{2x - 10}}}}$](img542.gif) .
.
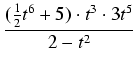 dt
dt
![$\displaystyle \sqrt[3]{{\frac{x + 1}{x - 1}}}$](img546.gif) .
. 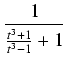 .
. 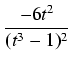 dt,
dt,