


Next: Całki funkcji zawierających pierwiastki
Up: Rachunek całkowy
Previous: Całki z funkcji wymiernych
Wszystkie "normalne" funkcje, w których występują funkcje trygonometryczne daje się zapisać jako
odpowiednie kombinacje sinusów i kosinusów, wystarczy więc wiedzieć, w jaki sposób obliczać tego typu
całki. Istnieje ogólna metoda, która pozwala radzić sobie z takimi przypadkami - omówimy ją pod koniec
paragrafu. Ogólne metody często są niewygodne w użyciu, zaczniemy więc od omówienia pewnych klas funkcji
trygonometrzycznych, w przypadku których można stosunkowo łatwo sobie poradzić stosując odpowiednie sztuczki.
Całki postaci
 f (x)ndx, gdzie f jest funkcją trygonometryczną (lub jej odwrotnością) a n jest
pewną liczbą naturalną. Całki tego typu obliczamy stusując następujące wzory rekurencyjne:
f (x)ndx, gdzie f jest funkcją trygonometryczną (lub jej odwrotnością) a n jest
pewną liczbą naturalną. Całki tego typu obliczamy stusując następujące wzory rekurencyjne:
-
 sinn(x)dx = -
sinn(x)dx = - 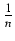 sinn-1(x)cos(x) +
sinn-1(x)cos(x) + 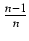
 sinn-2(x)dx
sinn-2(x)dx
-
 cosn(x)dx =
cosn(x)dx = 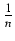 cosn-1(x)sin(x) +
cosn-1(x)sin(x) + 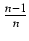
 cosn-2(x)dx
cosn-2(x)dx
-
 tgn(x)dx =
tgn(x)dx = 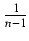 tgn-1(x) -
tgn-1(x) -  tgn-2(x)dx
tgn-2(x)dx
-
 ctgn(x)dx = -
ctgn(x)dx = - 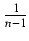 ctgn-1(x) -
ctgn-1(x) -  ctgn-2(x)dx
ctgn-2(x)dx
-

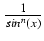 dx = -
dx = - 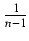
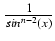 ctg(x) +
ctg(x) + 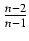

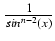 dx
dx
-

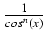 dx =
dx = 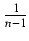
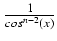 tg(x) +
tg(x) + 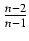

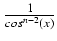 dx
dx
Wzorów tych łatwo dowodzi się z wykorzystaniem całkowania przez części i podstawowych tożsamości trygonometrycznych.
Przykład: Udowodnić wzór:
 sinn
sinn(
x)
dx = -
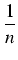 sinn-1
sinn-1(
x)
cos(
x) +
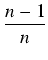
 sinn-2
sinn-2(
x)
dx.
Oznaczmy
In =  sinn(x)dx zapiszmy całkę w postaci:
sinn(x)dx zapiszmy całkę w postaci:
In =
 sinn-1
sinn-1(
x)
sin(
x)
dx.
Całkujemy przez części przyjmując:
u(x) = sinn-1(x),
v'(x) = sinx, skąd
u'(x) = (n - 1)sinn-2(x)cos(x),
v(x) = - sin(x).
Stąd:
| In |
= |
- sinn-1(x)cos(x) + (n - 1) sinn-2(x)cos2(x)dx = sinn-2(x)cos2(x)dx = |
|
| |
= |
- sinn-1(x)cos(x) + (n - 1) sinn-2(x)(1 - sin2(x))dx = sinn-2(x)(1 - sin2(x))dx = |
|
| |
= |
- sinn-1(x)cos(x) + (n - 1) sinn-2(x)dx - (n - 1) sinn-2(x)dx - (n - 1) sinn(x)dx sinn(x)dx |
|
co inaczej można zapisać jako:
In = - sinn-1(x)cos(x) + (n - 1)In-2 - (n - 1)In.
Po zredukowaniu wyrazu podobnego In i podzieleniu obydwu stron przez n otrzymujemy żądaną równość.
Zamiast stosować wzory rekurencyjne można czasem zastosować inne tricki:
Przykład: Obliczyć całkę
 sin17
sin17(
x)
dx.
Ośmiokrotne iterowanie wzoru nie wydaje się dobrym pomysłem; zamiast tego zapiszmy:
 sin17
sin17(
x)
dx =

(
sin2(
x))
6sin(
x)
dx =

(1 -
cos2(
x))
6sin(
x)
dx
i zastosujmy podstawienie
u = cos(x). Stąd
du = - sin(x)dx i otrzymujemy:
 sin17
sin17(
x)
dx = -

(1 -
u2)
6du,
a więc łatwą do policzenia całkę z wielomianu.
W przypadku stosowania wzorów rekurencyjnych w ostatnim kroku otrzymujemy bądź całkę z funkcji stałej,
bądź całkę elementarną z funkcji trygonometrycznej.
Całki postaci
 f (Ax)ng(Bx)mdx, gdzie f oraz g są sinusem i/lub kosinusem. W ogólnym przypadku
całki te sprowadzamy do sumy całek wcześniej omówionego typu stosując w tym celu odpowiednie tożsamości
trygonometryczne.
f (Ax)ng(Bx)mdx, gdzie f oraz g są sinusem i/lub kosinusem. W ogólnym przypadku
całki te sprowadzamy do sumy całek wcześniej omówionego typu stosując w tym celu odpowiednie tożsamości
trygonometryczne.
W pierwszym kroku redukujemy potęgi używając identyczności:
sin(
x)
cos(
x) =
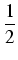 sin
sin(2
x),
sin2(
x) =
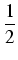
(1 -
cos(2
x)),
cos2(
x) =
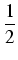
(1 +
cos(2
x)).
Najpierw eliminujemy iloczyny postaci
sin(Ax)cos(Ax) za pomocą pierwszego wzoru, a potem - przy pomocy
dwóch pozostałych - "zmniejszamy o połowę" występujące potęgi. Po tym procesie zostają nam iloczyny
postaci
f (Ax)g(Bx) gdzie A 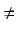 B. W drugim kroku rozbijamy je używając następujących wzorów:
B. W drugim kroku rozbijamy je używając następujących wzorów:
sin(
Ax)
sin(
Bx) =
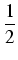
(
cos((
A -
B)
x) -
cos((
A +
B)
x)),
cos(
Ax)
cos(
Bx) =
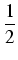
(
cos((
A -
B)
x) +
cos((
A +
B)
x)),
sin(
Ax)
cos(
Bx) =
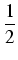
(
sin((
A -
B)
x) +
sin((
A +
B)
x)).
Przykład: Obliczyć całkę:
 cos2
cos2(2
x)
sin(
x)
dx.
Stosując powyższe uwagi mamy kolejno:
 cos2(2x)sin(x)dx cos2(2x)sin(x)dx |
= |
 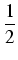 (1 + cos(4x))sin(x)dx = (1 + cos(4x))sin(x)dx = |
|
| |
= |
 ( (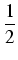 cos(4x) + cos(4x) + 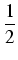 sin(x)cos(4x))dx = sin(x)cos(4x))dx = |
|
| |
= |
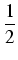  cos(4x)dx + cos(4x)dx + 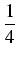  (sin(- 3x) + sin(7x))dx = (sin(- 3x) + sin(7x))dx = |
|
| |
= |
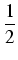  cos(4x)dx + cos(4x)dx + 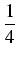  sin(- 3x)dx + sin(- 3x)dx + 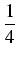  sin(7x)dx. sin(7x)dx. |
|
Pozostałe całki liczymy już bezpośrednio stosując oczywiste podstawienia u = 4x, v = - 3x i t = 7x
dla każdej z nich.
Czasem zamiast redukować wyrażenia postaci
sin(Ax)cos(Ax), można pójść krótszą drogą:
- Jeżeli w całce
 sinn(Ax)cosm(Ax)dx liczba m = 2k + 1 jest nieparzysta, to piszemy:
sinn(Ax)cosm(Ax)dx liczba m = 2k + 1 jest nieparzysta, to piszemy:
 sinn
sinn(
Ax)
cosm(
Ax)
dx =
 sinn
sinn(
Ax)(
cos2(
Ax))
kcos(
Ax)
dx =
 sinn
sinn(
Ax)(1 -
sin2(
Ax))
kcos(
Ax)
dx
i stosujemy podstawienie
u = sinAx.
- Jeżeli w całce
 sinn(Ax)cosm(Ax)dx liczba n = 2k + 1 jest nieparzysta, to piszemy:
sinn(Ax)cosm(Ax)dx liczba n = 2k + 1 jest nieparzysta, to piszemy:
 sinn
sinn(
Ax)
cosm(
Ax)
dx =

(
sin2(
Ax))
kcosm(
Ax)
sin(
Ax)
dx =

(1 -
cos2(
Ax))
kcosm(
Ax)
sin(
Ax)
dx
i stosujemy podstawienie
u = cosAx.
Przykład: Obliczyć całkę:
 sin5
sin5(
x)
cos2(
x)
dx.
Stosując się do powyższych uwag mamy kolejno:
 sin5(x)cos2(x)dx sin5(x)cos2(x)dx |
= |
 (sin2(x))2cos2(x)sin(x)dx = (sin2(x))2cos2(x)sin(x)dx = |
|
| |
= |
 (1 - cos2(x))2sin(x)dx = (1 - cos2(x))2sin(x)dx = |
|
| |
= |
-  (1 - u2)u2du. (1 - u2)u2du. |
|
Dalsze obliczenia łatwo doprowadzić do końca pamiętając o tym, że
u = cos(x).
Inny przykład pomysłowego tricku to całki z wyrażeń postaci
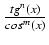 :
:
- Jeżeli w całce

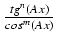 dx liczba m = 2k jest parzysta, to piszemy:
dx liczba m = 2k jest parzysta, to piszemy:

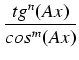 dx
dx =

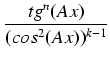 .
. 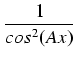 dx
dx =
 tgn
tgn(
Ax)
. (1 +
tg2(
Ax))
k-1 . 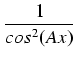 dx
dx
i stosujemy podstawienie
u = tg(Ax) (wykorzystaliśmy tu równość
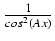 =
= 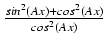 = tg2(Ax) + 1).
= tg2(Ax) + 1).
- Jeżeli w całce

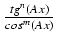 dx liczba n = 2k + 1 jest nieparzysta, to piszemy:
dx liczba n = 2k + 1 jest nieparzysta, to piszemy:

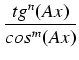 dx
dx =

(
tg2(
Ax))
k . 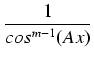 .
. 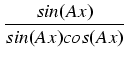 dx
dx =

(
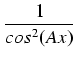
-1)
. 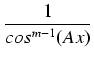 .
. 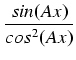 dx
dx
i stosujemy podstawienie
u = 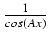 ; wówczas
du = -
; wówczas
du = - 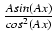 .
.
Przykład: Obliczyć całkę:

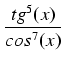 dx
dx.
Stosując się do powyższych uwag mamy kolejno:
 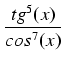 dx dx |
= |
 tg4(x) . tg4(x) . 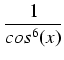 . . 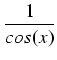 . tg(x)dx = . tg(x)dx = |
|
| |
= |
 ( (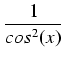 -1)2 . -1)2 . 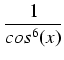 . . 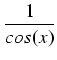 . tg(x)dx = . tg(x)dx = |
|
| |
= |
 (u2 -1)2u6du. (u2 -1)2u6du. |
|
Dalsze obliczenia łatwo doprowadzić do końca pamiętając o tym, że
u = 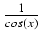 .
.
Całki postaci
 R(sin(x), cos(x))dx, gdzie R jest funkcją wymierną dwóch zmiennych. Podamy
ogólną metodę rozwiązywania całek z funkcji wymiernych od funkcji trygonometrycznych. Metoda ta jest
na ogół dość czasochłonna i o ile jest to tylko możliwe, wskazane jest używanie uproszczonych schematów
opisanych powyżej. O ile nie jest to możliwe, stosujemy podstawienie:
R(sin(x), cos(x))dx, gdzie R jest funkcją wymierną dwóch zmiennych. Podamy
ogólną metodę rozwiązywania całek z funkcji wymiernych od funkcji trygonometrycznych. Metoda ta jest
na ogół dość czasochłonna i o ile jest to tylko możliwe, wskazane jest używanie uproszczonych schematów
opisanych powyżej. O ile nie jest to możliwe, stosujemy podstawienie:
u =
tg(
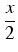
).
Wówczas funkcje trygonometryczne zmiennej x wyrażą się - poprzez proste tożsamości trygonometryczne -
następującymi wzorami:
-
sin(x) =
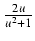 ,
,
-
cos(x) =
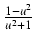 ,
,
-
tg(x) =
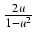 ,
,
-
ctg(x) =
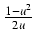 ,
,
-
dx =
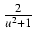 du.
du.
Przykład: Obliczyć całkę:

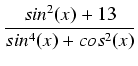 dx
dx.
Stosując uniwersalne podstawienie trygonometryczne otrzymujemy:
Dalsze obliczenia sprowadzają się do znalezienia całki z funkcji wymiernej.
Ćwiczenia:
-
 sin4(x)dx Odpowiedź:
-
sin4(x)dx Odpowiedź:
- 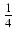 cos(x)sin(x)(sin2(x) +
cos(x)sin(x)(sin2(x) + 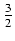 ) +
) + 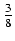 x + C
x + C
-

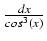 Odpowiedź:
Odpowiedź:
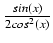 +
+ 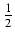 ln| tg(
ln| tg(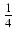
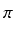 +
+ 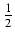 x)| + C
x)| + C
-
 ctg6(x)dx Odpowiedź:
-
ctg6(x)dx Odpowiedź:
- 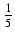 ctg5(x) +
ctg5(x) + 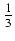 ctg3(x) - ctg(x) - x + C
ctg3(x) - ctg(x) - x + C
-
 cos(2x)sin(4x)dx Odpowiedź:
-
cos(2x)sin(4x)dx Odpowiedź:
- 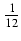 cos(6x) -
cos(6x) - 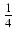 sin(2x) + C
sin(2x) + C
-
 sin(5x)sin(2x)dx Odpowiedź:
sin(5x)sin(2x)dx Odpowiedź:
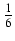 sin(3x) -
sin(3x) - 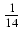 sin(7x) + C
sin(7x) + C
-
 sin(x)tg(x)dx Odpowiedź:
ln| tg(
sin(x)tg(x)dx Odpowiedź:
ln| tg(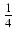 x +
x + 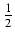 x)| - sin(x) + C
x)| - sin(x) + C
-
 sin5(x)cos2(x)dx Odpowiedź:
sin5(x)cos2(x)dx Odpowiedź:
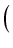 sin6(x) -
sin6(x) - 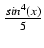 -
- 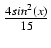 -
- 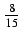
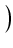
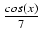 + C
+ C
-

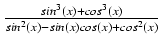 dx Odpowiedź:
sin(x) - cos(x) + C
dx Odpowiedź:
sin(x) - cos(x) + C
-

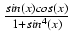 dx Odpowiedź:
dx Odpowiedź:
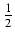 arctg(2tg2(x) + 1) + C
arctg(2tg2(x) + 1) + C
-

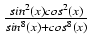 dx Odpowiedź:
dx Odpowiedź:
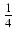
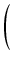
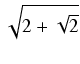 arctg
arctg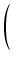
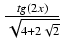
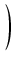 -
- 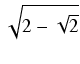 arctg
arctg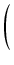
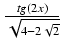
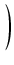
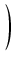 + C
+ C



Next: Całki funkcji zawierających pierwiastki
Up: Rachunek całkowy
Previous: Całki z funkcji wymiernych
Pawel Gladki
2006-01-30
![]() f (x)ndx, gdzie f jest funkcją trygonometryczną (lub jej odwrotnością) a n jest
pewną liczbą naturalną. Całki tego typu obliczamy stusując następujące wzory rekurencyjne:
f (x)ndx, gdzie f jest funkcją trygonometryczną (lub jej odwrotnością) a n jest
pewną liczbą naturalną. Całki tego typu obliczamy stusując następujące wzory rekurencyjne:
![]() f (Ax)ng(Bx)mdx, gdzie f oraz g są sinusem i/lub kosinusem. W ogólnym przypadku
całki te sprowadzamy do sumy całek wcześniej omówionego typu stosując w tym celu odpowiednie tożsamości
trygonometryczne.
f (Ax)ng(Bx)mdx, gdzie f oraz g są sinusem i/lub kosinusem. W ogólnym przypadku
całki te sprowadzamy do sumy całek wcześniej omówionego typu stosując w tym celu odpowiednie tożsamości
trygonometryczne.
![]() :
:
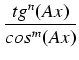 dx =
dx = 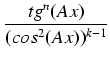 .
. 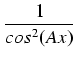 dx =
dx = 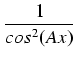 dx
dx
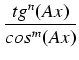 dx =
dx = 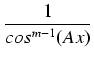 .
. 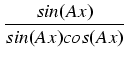 dx =
dx = 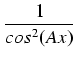 -1) .
-1) . 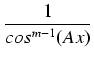 .
. 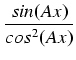 dx
dx
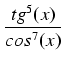 dx.
dx.
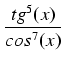 dx
dx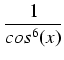 .
. 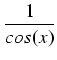 . tg(x)dx =
. tg(x)dx =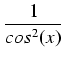 -1)2 .
-1)2 . 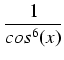 .
. 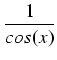 . tg(x)dx =
. tg(x)dx =![]() R(sin(x), cos(x))dx, gdzie R jest funkcją wymierną dwóch zmiennych. Podamy
ogólną metodę rozwiązywania całek z funkcji wymiernych od funkcji trygonometrycznych. Metoda ta jest
na ogół dość czasochłonna i o ile jest to tylko możliwe, wskazane jest używanie uproszczonych schematów
opisanych powyżej. O ile nie jest to możliwe, stosujemy podstawienie:
R(sin(x), cos(x))dx, gdzie R jest funkcją wymierną dwóch zmiennych. Podamy
ogólną metodę rozwiązywania całek z funkcji wymiernych od funkcji trygonometrycznych. Metoda ta jest
na ogół dość czasochłonna i o ile jest to tylko możliwe, wskazane jest używanie uproszczonych schematów
opisanych powyżej. O ile nie jest to możliwe, stosujemy podstawienie:
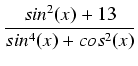 dx.
dx.
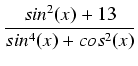 dx
dx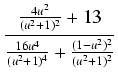 .
. 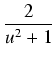 du =
du =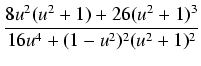 du.
du.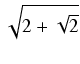 arctg
arctg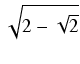 arctg
arctg