


Next: Niewymierność pierwiastków z liczb
Up: Liczby rzeczywiste
Previous: Jak obliczyć log35?
Liczbę e (tj. liczbę Eulera) można określić jako granicę pewnego ciągu liczbowego. Otóż można
udowodnię, że ciąg o wyrazie ogólnym
jest rosnący i ograniczony z góry, a więc ma granicę (Twierdzenie: Każdy ciąg liczbowy rosnący
i ograniczony z góry ma granicę) - dowód ten zwykle poznaje się na pierwszym kursie analizy
i znaleźć go można w prawie każdym podręczniku, na przykład W. Kołodziej, Analiza matematyczna,
PWN, Warszawa 1978, str. 41. Ją właśnie oznaczamy przez e. Symbol ten wprowadził w 1736 roku
L. Euler (1707-1783).
Liczba e jest niewymierna; jej niewymierność wykazał J. H. Lambert (1728-1777) w 1766 r.
Podamy prosty dowód J. Fouriera (1768-1830) z 1815 roku - wykorzystamy rozwinięcie liczby e
w szereg:
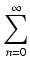
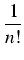
.
Załóżmy nie wprost, że
e = 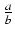 ,
NWD(a, b) = 1, a, b - naturalne. Niech N
,
NWD(a, b) = 1, a, b - naturalne. Niech N  b.
Oznaczmy:
Zauważmy, że b dzieli N! i że
b.
Oznaczmy:
Zauważmy, że b dzieli N! i że 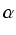 jest liczbą naturalną. Z drugiej strony:
jest liczbą naturalną. Z drugiej strony:
| 0 |
< |
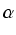 = N!( = N!(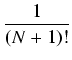 + + 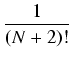 +...) = +...) = |
|
| |
= |
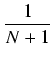 + + 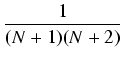 +...< +...< |
|
| |
< |
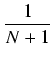 + + 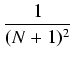 +...= +...= 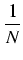 |
|
jako suma ciągu geometrycznego. Otrzymaliśmy sprzeczność: 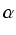 jest liczbą naturalną i zarazem:
jest liczbą naturalną i zarazem:
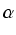
<
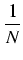
< 1.
Liczba e ma wartość przybliżoną ok. 2.718281828459 - została ona podana w 1728 roku przez Daniela
Bernoulli (1700-1782). Przybliżoną wartość liczby e moźna obliczyć z dowolną dokładnościa
według wzoru
Błąd bezwzględny tego przybliżenia nie przekracza liczby 3/n!. Na przykład aby
obliczyć e z dokładnością do 0,0001 musimy wziąć n = 8 (jest to najmniejsza liczba naturalna n,
dla której
3/n! < 0.0001) i obliczyć sumę:
Ogólniej, znany jest wzór:
Ponieważ 0! = 1, więc powyższe można zapisać jako:
ex =
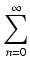
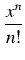
- jest to rozwinięcie funkcji wykładniczej
f (x) = ex w tzw. szereg Maclaurina (C. Maclaurin, 1698-1746).
Czasami stosuje się oznaczenie
ex = exp(x) (exponent to po angielsku wykładnik, po łacinie
wykładnik to exponens, exponentis). Funkcja wykładnicza
f (x) = ex ma pochodną równa sobie
samej, tzn.
f'(x) = ex - to również fakt znany z podręczników, zob. np. W. Kołodziej, Analiza
matematyczna, PWN, Warszawa 1978, str. 150.
Jest też e liczbą przestepną, tzn. nie jest pierwiastkiem żadnego wielomianu o współczynnikach całkowitych.
Przestępność liczby e wykazał Ch. Hermite (1822-1901) w roku 1873 (Ch. Hermite, Sur la fonction
exponentielle, C.R. Acad. Sci. (Paris), 1873, 77, strony: 18-24, 74-79, 226-233, 285-293). Przytoczymy
prosty dowód tego faktu pochodzący od Hurwitza z 1892 roku.
Przypuśćmy nie wprost, że e jest liczbą algebraiczną, a więc że istnieją liczby całkowite
i względnie pierwsze
C0,..., Cn takie, że:
Cnen +...+ C1e + C0 = 0.
Niech p będzie liczbą pierwszą większą zarówno od C0 jak i od n.
Zdefiniujmy wielomian f wzorem:
f (
x) =
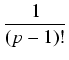 xp-1
xp-1(1 -
x)
p(2 -
x)
p...(
n -
x)
p.
Ponieważ zero jest p - 1-krotnym pierwiastkiem f, więc
f(s)(0) = 0
dla
s = 0, 1,..., p - 2. Podobnie, ponieważ każda z liczb k (
k = 1, 2,..., n) jest p-krotnym
pierwiastkiem f, więc:
f(s)(k) = 0
dla
s = 0, 1,..., p - 1,
k = 0, 1,..., n. Ponadto:
f(p-1)(0) = (n!)p.
Jasne jest, że współczynniki s-tej pochodnej wielomianu o całkowitych współczynnikach są podzielne
przez s!, a więc w szczególności współczynniki pochodnej rzędu s wielomianu:
xp-1(1 - x)p(2 - x)p...(n - x)p
są podzielne przez s!. Stąd wynika, że
f(s)(x) ma dla s  p współczynniki całkowite,
podzielne przez p. Niech teraz:
p współczynniki całkowite,
podzielne przez p. Niech teraz:
F(x) = f (x) + f'(x) + f''(x) +...+ f (N)(x)
gdzie
N = deg f. Zatem:
F(0) jest całkowite i niepodzielne przez p
oraz
F(k) jest całkowite i podzielne przez p dla k = 1, 2,..., n.
Istotnie, mamy
N = np + p - 1. Wówczas:
F(0) =
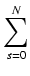 f(s)
f(s)(0) =
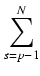 f(s)
f(s)(0) =
f(p-1) +
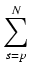 f(s)
f(s)(0) = (
n!)
p +
pA
gdzie A jest pewną liczbą całkowitą (każdy składnik sumy jest podzielny przez p), co dowodzi pierwszej równości.
Dla dowodu drugiej zauważmy, że:
F(
k) =
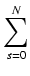 f(s)
f(s)(
k) =
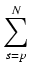 f(s)
f(s)(
k)
jest podzielne przez p, gdyż każdy składnik sumy jest podzielny przez p.
Zauważmy, że
(e-xF(x))' = e-xf (x). Niech
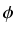 (x) = e-xF(x).
Wówczas - wobec tw. Lagrange'a o wartości średniej zastosowanego do przedziału [0, x] stwierdzamy,
że istnieje liczba
0 <
(x) = e-xF(x).
Wówczas - wobec tw. Lagrange'a o wartości średniej zastosowanego do przedziału [0, x] stwierdzamy,
że istnieje liczba
0 < 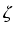 < 1 taka, że:
< 1 taka, że:
e-xF(
x) -
F(0) = -
xe-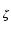 xf
xf (
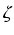 x
x)
tzn.
F(
x) -
exF(0) = -
xe(1-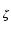 )xf
)xf (
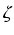 x
x).
W równości tej podstawmy
x = 1, 2,..., n. Otrzymujemy:
| F(1) - eF(0) |
= |
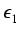 |
| F(2) - e2F(0) |
= |
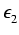 |
| |
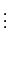 |
|
| F(n) - enF(0) |
= |
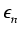 |
gdzie
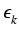 = - ke(1-
= - ke(1-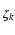 )kf (
)kf (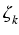 k) dla
k = 1, 2,..., n. Mnożąc pierwsze z powyższych równań
przez C1, drugie przez C2 itd. n-te przez Cn i dodając stronami otrzymujemy - w myśl naszego założenia:
k) dla
k = 1, 2,..., n. Mnożąc pierwsze z powyższych równań
przez C1, drugie przez C2 itd. n-te przez Cn i dodając stronami otrzymujemy - w myśl naszego założenia:
C0F(0) +
C1F(1) +...+
CnF(
n) =
C1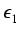
+...+
Cn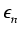
.
Lewa strona powyższego jest liczbą całkowitą różną od zera: p > C0, p nie dzieli F(0)
i dzieli pozostałe sładniki. Natomiast prawa strona dąży do zera wraz z p dążącym do nieskończoności.
Rzeczywiście, Ck jest stałe i nie zależy od p, zaś:
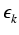 |
= |
- ke(1-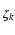 )kf ( )kf (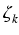 k) = k) = |
|
| |
= |
- ke(1-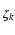 )k )k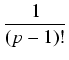 ( (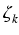 k)p-1(1 - k)p-1(1 - 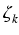 k)p...(n - k)p...(n - 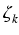 k)p = k)p = |
|
| |
= |
- 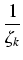 e(1- e(1-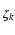 )k )k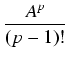 |
|
gdzie
A = 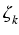 k(1 -
k(1 - 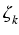 k)...(n -
k)...(n - 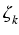 k), skąd wynika, że
k), skąd wynika, że
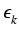 = stała .
= stała . 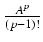 dąży do zera, gdy
p
dąży do zera, gdy
p 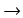
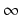 , dla
k = 1, 2,..., n. Niech p0 będzie taką liczbą pierwszą,
że dla każdej liczby pierwszej
p
, dla
k = 1, 2,..., n. Niech p0 będzie taką liczbą pierwszą,
że dla każdej liczby pierwszej
p  p0:
p0:
|
C1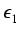
+...+
Cn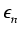
| < 1.
Liczba e "wzięła się" z logarytmów, a logarytmy wymyślono, żeby zamienić mnożenie na dodawanie.
Przez setki lat ta "cudowna własność" logarytmów, dzięki której z pomocą tablic (lub dwóch linijek
z logarytmiczna skala - skalę logarytmiczną wynalazł matematyk angielski E. Gunter w 1620 roku.
Suwak logarytmiczny wynalazł W. Oughtred około roku 1622) można było dodawać zamiast mnożyć (i mimo to uzyskiwać w rezultacie iloczyn)
ułatwiała ludziom zycie. Dziś, w epoce komputerów, to zastosowanie logarytmów ma mniejsze znaczenie
praktyczne. Logarytmy naturalne wzięły się stąd, że zostaly wymyślone jako "naturalny sposób"
owej zamiany mnozenia w dodawanie.
(1 + x)(1 + y) = 1 + x + y + xy
Dla małych x, y wyraz xy można pominąć i otrzymujemy
(1 +
x)(1 +
y)
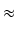
1 +
x +
y.
logarytm(1 +
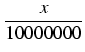
)
10000000 =
x
Zachodzi równość:
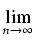
(1 +
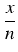
)
n =
ex.
Logarytmy, które po raz pierwszy pojawiły się na świecie w książce Johna Nepera
(albo - z francuskiego - Napiera, 1550-1617) "Mirifici logarithmorum canonis descriptio"
(Opis zadziwiających tablic logarytmów) z 1614 roku. Ta i druga jego ksiazka - "Mirifici logarithmorum canonis constructio"
(Budowa zadziwiających tablic logarytmów) z 1620 roku powstały przez stablicowanie wyrażeń
(1 + x/n)-n dla dużego n i x przebiegającego wyrazy ciągu arytmetycznego. Były więc
dobrymi przybliżeniami logarytmów przy podstawie e-1. Dziwna podstawa 1/e logarytmów Nepera
bierze się z faktu, że Neper obliczał przede wszystkim logarytmy sinusów posługując się "mechaniczną"
definicja funkcji odwrotnej do funkcji o wlasnosci
f'(x)/(1 - f (x)) = const.:
Mówimy, ze linia maleje proporcjonalnie, gdy punkt zakreślający takową w równych czasach
odcina części w stałym stosunku proporcjonalną do linii, od której zostały odcięte.
(tzn. gdy prędkość ruchu jest proporcjonalna do pozostałej części odcinka).
Jako że mogą być określone tak wolniejsze, jak i szybsze ruchy od dowolnie danego ruchu, wynika stąd
w konieczny sposób, że mogą być ruchy o równej chyżosci, co dowolny ruch (które określamy jako
nie szybsze i nie wolniejsze).
Zatem logarytm dowolnego sinusa jest liczbą najdokładniej wyrażającą linię, która przyrasta
równo w czasie, gdy linia [o długości] całego sinusa maleje proporcjonalnie, gdy oba ruchy są
równoczesne, i początkowo były równie szybkie.
Szwajcarski mechanik, zegarmistrz, astronom i matematyk J. Bürgi (1552-1632) odkrył logarytmy
wcześniej niż Neper, ale swoje tablice opublikował dopiero w 1620 roku pod tytulem
"Arytmetyczne i geometryczne tablice postępów". Bürgi obliczał (1 + x/n)n dla dużej
liczby n. W 1617 roku Henry Briggs (1561-1631) opublikował ułożone przez siebie tablice logarytmów
dziesiętnych liczb od 1 do 1000. Od 1617 roku Briggs (po spotkaniu z J. Neperem) w ciągu siedmiu lat
ułożył i wydał tablice logarytmów dziesiętnych liczb od 1 do 20 000 i od 90 000 do 100 000 z dokładnością
do 14 cyfr po przecinku. W książce "Brytyjska trygonometria" z 1633 roku Briggs zamieścił
logarytmy dziesiętne sinusów i tangensów z taką samą dokładnością. Z uwagi na ułatwienie obliczeń
mawiano, że Briggs wydłuzył dwukrotnie życie astronomom.
Felix Klein (1849-1925) definiował logarytm naturalny następująco:
ln
x =
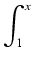
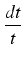
.
-
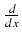 ln(xy) =
ln(xy) = 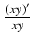 =
= 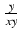 =
= 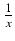
-
ln(xy) = ln x + c dla pewnej stałej c
-
ln(1 . y) = ln 1 + c = 0 + c
- ln y = c
-
ln(xy) = ln x + ln y.
Funkcje wykładnicze definiuje się wtedy tak:
ex =
y 
ln
y =
x
oraz
ax = exln a
dla a > 0.
Na koniec podamy przykład naturalnego pojawienia się liczby e. Jeśli złożyć w banku kwotę x
złotych na 10 procent rocznie na 10 lat, to po tym czasie mamy na koncie
(1 + 10 . 0, 10)x = (1 + 1)x = 2x.
Jeśli pilnujemy swoich interesów, to możemy sobie zażyczyć aktualizacji konta nie po całym okresie
lokaty, a co pół tego okresu - co 5 lat. Wtedy bank co 5 lat zwiększy nasze oszczędności o 50
procent (10 procent rocznie) i po 10 latach stan konta wyniesie
(1 + 0, 50)
2x = (1 +
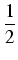
)
2x = 2, 25
x.
(1 + 0, 20)
5x = (1 +
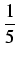
)
5x = 2, 48832
x.
(1 + 0, 10)
10x = (1 +
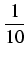
)
10x = 2, 5937424601
x.
(1 +
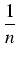
)
nx



Next: Niewymierność pierwiastków z liczb
Up: Liczby rzeczywiste
Previous: Jak obliczyć log35?
Pawel Gladki
2006-01-30
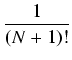 +
+ 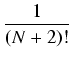 +...) =
+...) =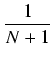 +
+ 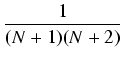 +...<
+...<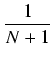 +
+ 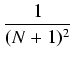 +...=
+...= 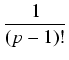 xp-1(1 - x)p(2 - x)p...(n - x)p.
xp-1(1 - x)p(2 - x)p...(n - x)p.
![]() (x) = e-xF(x).
Wówczas - wobec tw. Lagrange'a o wartości średniej zastosowanego do przedziału [0, x] stwierdzamy,
że istnieje liczba
0 <
(x) = e-xF(x).
Wówczas - wobec tw. Lagrange'a o wartości średniej zastosowanego do przedziału [0, x] stwierdzamy,
że istnieje liczba
0 < ![]() < 1 taka, że:
< 1 taka, że:
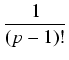 (
(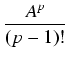
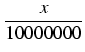 )10000000 = x
)10000000 = x