


Next: Pi-ematy, czyli jak zapamiętać
Up: Liczby rzeczywiste
Previous: Ułamek 0,(9)
Już Archimedes (ok. 287 - 212 pne.) OBLICZYŁ, że
czyli
3,(14084507042253521126760563380281690) <
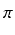
< 3, 142857(142857),
 z dokładnością do dwóch miejsc dziesiętnych po przecinku. Archimedes obliczył obwód
dziewiećdziesięciosześciokąta foremnego wpisanego w okrąg i opisanego na okręgu.
Pomiar obwodu koła sznurkiem daje wynik "przybliżony" 3,16 (takiej wartości używali starożytni
Rzymianie). Poniżej zamieszczamy obliczenie 1000 cyfr po przecinku w rozwinięciu dziesiętnym
z dokładnością do dwóch miejsc dziesiętnych po przecinku. Archimedes obliczył obwód
dziewiećdziesięciosześciokąta foremnego wpisanego w okrąg i opisanego na okręgu.
Pomiar obwodu koła sznurkiem daje wynik "przybliżony" 3,16 (takiej wartości używali starożytni
Rzymianie). Poniżej zamieszczamy obliczenie 1000 cyfr po przecinku w rozwinięciu dziesiętnym  ,
czyli
,
czyli  z błędem mniejszym od
10-1000. Błąd o jeden promień Bohra (najmniejszy możliwy
promień atomu wodoru) w pomiarze długości okręgu o promieniu jednego roku świetlnego to błąd rzędu
10-27, więc mówienie o pomiarach w tym kontekście jest bez sensu (promień Bohra =
5, 29 . 10-11 m, rok świetlny = 9 460 766 438 784 000 m).
z błędem mniejszym od
10-1000. Błąd o jeden promień Bohra (najmniejszy możliwy
promień atomu wodoru) w pomiarze długości okręgu o promieniu jednego roku świetlnego to błąd rzędu
10-27, więc mówienie o pomiarach w tym kontekście jest bez sensu (promień Bohra =
5, 29 . 10-11 m, rok świetlny = 9 460 766 438 784 000 m).
Najbardziej znaczącym osiągnieciem w zakresie bezpośredniego porównywania koła z wielokątem było
użycie przez Ludolfa van Ceulen (1540 - 1610), w 1582 r., wielokąta foremnego o 235 bokach, co
pozwoliło wyznaczyć 20 dokładnych cyfr rozwinięcia dziesiętnego liczby  . Swoje rezultaty
Ludolf van Ceulen opublikował w książce "O kole", wydanej w 1596, a po jego śmierci znaleziono
w jego zapiskach jeszcze 15 dalszych cyfr. Od połowy XVII w. znaleziono wiele szeregów, których
sumy wyrażają liczbę
. Swoje rezultaty
Ludolf van Ceulen opublikował w książce "O kole", wydanej w 1596, a po jego śmierci znaleziono
w jego zapiskach jeszcze 15 dalszych cyfr. Od połowy XVII w. znaleziono wiele szeregów, których
sumy wyrażają liczbę  , począwszy od szeregu Leibniza z 1673 r.:
, począwszy od szeregu Leibniza z 1673 r.:
opublikowanego w 1682 r. w "Acta Eruditorum".
Programiki, które NAPRAWDĘ liczą  (procedury do obliczania
(procedury do obliczania  z dowolną dokładnością) nie
korzystają z rozwinięć dziesiętnych liczb wymiernych, tylko z szeregów potęgowych. Dla obliczeń
z ograniczoną dokładnością (np. kalkulator) wystarczy rzeczywiście dobre przybliżenie wymierne,
np. każdy z ułamków:
z dowolną dokładnością) nie
korzystają z rozwinięć dziesiętnych liczb wymiernych, tylko z szeregów potęgowych. Dla obliczeń
z ograniczoną dokładnością (np. kalkulator) wystarczy rzeczywiście dobre przybliżenie wymierne,
np. każdy z ułamków:
przybliża  z błędem mniejszym, niż
1/(kwadrat mianownika), a ostatni z tych ułamków
gwarantuje, że żaden użytkownik kalkulatora w życiu nie natrafi na niedokładność. Takie przybliżenia
znajduje się za pomocą ułamków łańcuchowych. Przybliżenie liczby
z błędem mniejszym, niż
1/(kwadrat mianownika), a ostatni z tych ułamków
gwarantuje, że żaden użytkownik kalkulatora w życiu nie natrafi na niedokładność. Takie przybliżenia
znajduje się za pomocą ułamków łańcuchowych. Przybliżenie liczby  liczbami wymiernymi nie może
mieć "absolutnej" dokładności, bo liczba
liczbami wymiernymi nie może
mieć "absolutnej" dokładności, bo liczba  nie jest wymierna. Niewymierność
nie jest wymierna. Niewymierność  udowodnił
J. H. Lambert (1728 - 1777) w 1767 roku; jest nawet gorzej: Ferdynand Lindemann (1852 - 1939) udowodnił,
że żadna suma całkowitych wielokrotności potęg liczby
udowodnił
J. H. Lambert (1728 - 1777) w 1767 roku; jest nawet gorzej: Ferdynand Lindemann (1852 - 1939) udowodnił,
że żadna suma całkowitych wielokrotności potęg liczby  , w której występują inne potęgi niż
zerowa, nie jest liczbą całkowitą, tzn. że
, w której występują inne potęgi niż
zerowa, nie jest liczbą całkowitą, tzn. że  jest liczbą przestępną. Procedury obliczające
jest liczbą przestępną. Procedury obliczające
 podają przybliżoną wartość
podają przybliżoną wartość  z taką dokładnością, jakiej zażądano.
z taką dokładnością, jakiej zażądano.
Ile dokładnie wynosi liczba  ? Dokładnie, to jest równa stosunkowi długości okręgu do jego
średnicy. Nie wypiszemy tutaj pełnego rozwinięcia dziesiętnego
? Dokładnie, to jest równa stosunkowi długości okręgu do jego
średnicy. Nie wypiszemy tutaj pełnego rozwinięcia dziesiętnego  , bo nie mamy nieskończonego
czasu, ani nieskończonego miejsca. A Czytelnik nie ma nieskończonego czasu na czytanie nieskończonego
ciągu cyfr.
, bo nie mamy nieskończonego
czasu, ani nieskończonego miejsca. A Czytelnik nie ma nieskończonego czasu na czytanie nieskończonego
ciągu cyfr.
Jak obliczyć  z dowolną dokładnością? Liczbę
z dowolną dokładnością? Liczbę  najwygodniej przedstawić jako
najwygodniej przedstawić jako
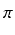
= 4 arctan 1
a następnie wykorzystać (odkryty w 1670 przez Jamesa Gregory) szereg Taylora dla funkcji
f (x) = arctan x:
arctan
x =
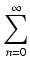
(- 1)
n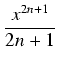
=
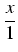
-
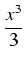
+
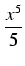
-
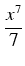
+...
Aby mieć wzór na  dający szybko dobre przybliżenie, korzystamy ze wzoru
dający szybko dobre przybliżenie, korzystamy ze wzoru
arctan
x + arctan
y = arctan
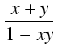
 0, xy < 1, który jest inaczej zapisanym wzorem (odkrytym przez J. Machina) na
tangens sumy. Metoda Johna Machina (1680 - 1751) polega na następującym wyborze kątów:
0, xy < 1, który jest inaczej zapisanym wzorem (odkrytym przez J. Machina) na
tangens sumy. Metoda Johna Machina (1680 - 1751) polega na następującym wyborze kątów:
2 arctan
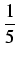
= arctan
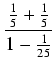
= arctan
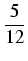
4 arctan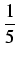 |
= |
2 arctan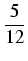 = arctan = arctan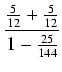 = arctan = arctan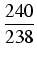 = = |
|
| |
= |
arctan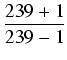 = arctan = arctan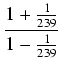 = arctan 1 + arctan = arctan 1 + arctan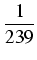 |
|
Stąd:
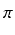 |
= |
4 arctan 1 = 4(4 arctan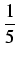 - arctan - arctan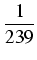 ) = ) = |
|
| |
= |
16 arctan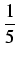 -4 arctan -4 arctan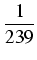 |
|
i stosując rozwinięcia w szeregi potęgowe:
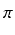 |
= |
16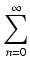 (- 1)n (- 1)n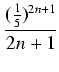 -4 -4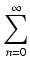 (- 1)n (- 1)n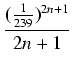 = = |
|
| |
= |
16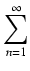 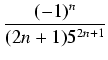 -4 -4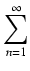 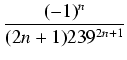 |
|
Żeby na przykład obliczyć 1000 dokładnych cyfr po przecinku w rozwinięciu dziesiętnym  trzeba
zsumować tyle składników, żeby błąd był mniejszy od
1/101000, to znaczy
dla pierwszego szeregu i
trzeba
zsumować tyle składników, żeby błąd był mniejszy od
1/101000, to znaczy
dla pierwszego szeregu i
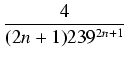
<
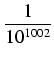
dla drugiego szeregu. Wystarczy uwzględnić np. 1001 składników pierwszego szeregu
(1/5 < 1/2) i 501 składników drugiego szeregu (
1/239 < 1/102). W rzeczywistości wystarczy
znacznie mniej składników, np.
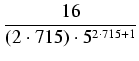
<
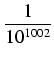
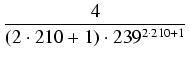
<
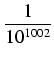
czyli wystarczy 714 składników pierwszego szeregu i 209 składników drugiego szeregu. Każdy ze składników
należy obliczać z błędem mniejszym od
1/101003, bo liczba skladników przekracza 1000.
Ostatecznie pierwszych tysiąc cyfr po przecinku w rozwinięciu dziesiętnym liczby  to pierwsze
tysiąc cyfr po przecinku liczby
Obliczenia wykonane za pomocą GP Pari dają w wyniku:
to pierwsze
tysiąc cyfr po przecinku liczby
Obliczenia wykonane za pomocą GP Pari dają w wyniku:
3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899
86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502
84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165
27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817
48815 20920 96282 92540 91715 36436 78925 90360 01133 05305 48820 46652 13841 46951 94151 16094
33057 27036 57595 91953 09218 61173 81932 61179 31051 18548 07446 23799 62749 56735 18857 52724
89122 79381 83011 94912 98336 73362 44065 66430 86021 39494 63952 24737 19070 21798 60943 70277
05392 17176 29317 67523 84674 81846 76694 05132 00056 81271 45263 56082 77857 71342 75778 96091
73637 17872 14684 40901 22495 34301 46549 58537 10507 92279 68925 89235 42019 95611 21290 21960
86403 44181 59813 62977 47713 09960 51870 72113 49999 99837 29780 49951 05973 17328 16096 31859
50244 59455 34690 83026 42522 30825 33446 85035 26193 11881 71010 00313 78387 52886 58753 32083
81420 61717 76691 47303 59825 34904 28755 46873 11595 62863 88235 37875 93751 95778 18577 80532
17122 68066 13001 92787 66111 95909 21642 01989 38
John Machin za pomocą tego szeregu ręcznie obliczył 100 cyfr dziesiętnych liczby  , a sam szereg
(bez wyprowadzenia) William Jones zamiescił w swoim "Synopsis palmariorum matheseos" w 1706 roku
(tam właśnie po raz pierwszy użyto symbolu
, a sam szereg
(bez wyprowadzenia) William Jones zamiescił w swoim "Synopsis palmariorum matheseos" w 1706 roku
(tam właśnie po raz pierwszy użyto symbolu  ).
).



Next: Pi-ematy, czyli jak zapamiętać
Up: Liczby rzeczywiste
Previous: Ułamek 0,(9)
Pawel Gladki
2006-01-30
![]() . Swoje rezultaty
Ludolf van Ceulen opublikował w książce "O kole", wydanej w 1596, a po jego śmierci znaleziono
w jego zapiskach jeszcze 15 dalszych cyfr. Od połowy XVII w. znaleziono wiele szeregów, których
sumy wyrażają liczbę
. Swoje rezultaty
Ludolf van Ceulen opublikował w książce "O kole", wydanej w 1596, a po jego śmierci znaleziono
w jego zapiskach jeszcze 15 dalszych cyfr. Od połowy XVII w. znaleziono wiele szeregów, których
sumy wyrażają liczbę ![]() , począwszy od szeregu Leibniza z 1673 r.:
, począwszy od szeregu Leibniza z 1673 r.:
![]() (procedury do obliczania
(procedury do obliczania ![]() z dowolną dokładnością) nie
korzystają z rozwinięć dziesiętnych liczb wymiernych, tylko z szeregów potęgowych. Dla obliczeń
z ograniczoną dokładnością (np. kalkulator) wystarczy rzeczywiście dobre przybliżenie wymierne,
np. każdy z ułamków:
z dowolną dokładnością) nie
korzystają z rozwinięć dziesiętnych liczb wymiernych, tylko z szeregów potęgowych. Dla obliczeń
z ograniczoną dokładnością (np. kalkulator) wystarczy rzeczywiście dobre przybliżenie wymierne,
np. każdy z ułamków:
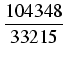 ,
,
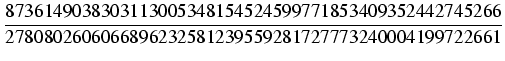
![]() ? Dokładnie, to jest równa stosunkowi długości okręgu do jego
średnicy. Nie wypiszemy tutaj pełnego rozwinięcia dziesiętnego
? Dokładnie, to jest równa stosunkowi długości okręgu do jego
średnicy. Nie wypiszemy tutaj pełnego rozwinięcia dziesiętnego ![]() , bo nie mamy nieskończonego
czasu, ani nieskończonego miejsca. A Czytelnik nie ma nieskończonego czasu na czytanie nieskończonego
ciągu cyfr.
, bo nie mamy nieskończonego
czasu, ani nieskończonego miejsca. A Czytelnik nie ma nieskończonego czasu na czytanie nieskończonego
ciągu cyfr.
![]() z dowolną dokładnością? Liczbę
z dowolną dokładnością? Liczbę ![]() najwygodniej przedstawić jako
najwygodniej przedstawić jako
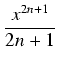 =
= ![]() dający szybko dobre przybliżenie, korzystamy ze wzoru
dający szybko dobre przybliżenie, korzystamy ze wzoru
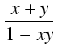
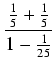 = arctan
= arctan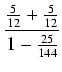 = arctan
= arctan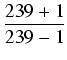 = arctan
= arctan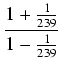 = arctan 1 + arctan
= arctan 1 + arctan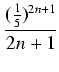 -4
-4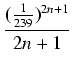 =
=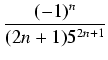 -4
-4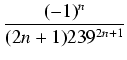
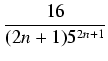 <
< 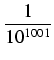 =
= 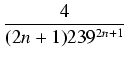 <
< 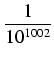
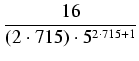 <
< 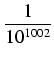
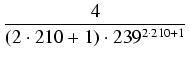 <
< 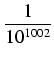
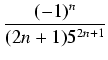 -4
-4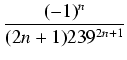
![]() , a sam szereg
(bez wyprowadzenia) William Jones zamiescił w swoim "Synopsis palmariorum matheseos" w 1706 roku
(tam właśnie po raz pierwszy użyto symbolu
, a sam szereg
(bez wyprowadzenia) William Jones zamiescił w swoim "Synopsis palmariorum matheseos" w 1706 roku
(tam właśnie po raz pierwszy użyto symbolu ![]() ).
).