


Next: Teoria liczb
Up: Rozwiązywanie równań
Previous: Wzory na pierwiastki dowolnego
Rozważmy wielomian
f (X) = a0Xn + a1Xn-1 +...+ an-1X + a0
w którym
a0 = an, a1 = an-1, a2 = an-2,...
i który nazywać będziemy wielomianem obustronnym.
Zauważmy, że wielomiany tego typu można scharakteryzować poprzez następującą własność:
Xnf (
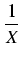
) =
f (
X).
Jeżeli teraz n jest liczbą nieparzystą, to oczywiście -1 jest pierwiastkiem równania f (X) = 0
i tym samym f (X) jest podzielny przez X + 1:
f (X) = (X + 1) . g(X).
Wielomian g(X) jest wielomianem stopnia n - 1 oraz:
Xn-1g(
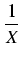
) =
Xn-1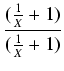 g
g(
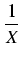
) =
Xn-1f (
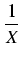
)
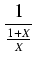
=
Xnf (
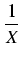
)
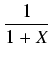
=
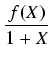
=
g(
X)
tak więc również wielomian g jest obustronny. Wobec tego przy badaniu wielomianów obustronnych wystarczy
ograniczyć się do przypadku wielomianów stopnia parzystego. Zanim pokażemy na czym polega ogólna sztuczka, rozważmy
konkretny przykład: rozwiążmy równanie:
6X4 = 35X3 +62X2 - 35X + 6 = 0.
Dzieląc przez X2 i odpowiednio porządkując składniki otrzymujemy:
6(
X2 +
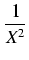
) - 35(
X +
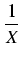
) + 62 = 0.
X +
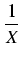
=
Z
wobec
X2 +
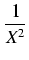
=
Z2 - 2
otrzymujemy
6(X2 - 2) - 35Z + 62 = 0,
a więc zwykłe równanie kwadratowe, które rozwiązujemy znanymi metodami.
Przejdźmy teraz do opisu ogólnej metody. Przed podaniem głównego twierdzenia sformułujmy lemat:
Lemat: Zachodzi równość:
Xk +
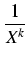
=
fk(
X +
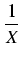
),
gdzie fk(X) są wielomianami otrzymanymi rekurencyjnie w następujący sposób:
f0(Z) = 2, f1(Z) = Z
oraz
fk+1(
Z) =
zfk(
Z) -
fk-1(
Z),
k 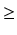
2.
Dowód: Faktycznie, dla k = 0 oraz k = 1 nie ma czego dowodzić - załóżmy więc, że równość zachodzi
dla liczb k - 1 i k. Ponieważ:
Xk+1 +
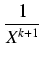
= (
Xk +
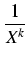
)(
X +
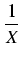
) - (
Xk-1 +
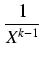
)
otrzymujemy:
Xk+1 +
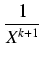
=
fk(
X +
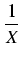
)(
X +
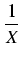
) -
fk-1(
X +
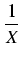
) =
fk+1(
X +
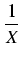
).
Z wykorzystaniem powyższego lematu udowodnimy następujące:
Twierdzenie: Jeśli n = 2m i
a0 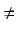 0, to pierwiastki wielomianu obustronnego:
0, to pierwiastki wielomianu obustronnego:
f (X) = a0Xn + a1Xn-1 +...+ an-1X + a0
można otrzymać rozwiązując równania kwadratowe:
X2 - ZjX + 1 = 0
dla
j = 1, 2,..., m, gdzie
Z1, Z2,..., Zm są rozwiązaniami równania:
a0fm(Z) + a1fm-1(Z) +...+ am-1f1(Z) + am = 0,
gdzie wielomiant
f1,..., fm są zdefiniowane tak, jak w poprzednim lemacie.
Dowód: Powiedzmy, że X0 jest jednym z pierwiastków rozważanego równania. Wówczac oczywiście
X0 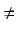 0, gdyż
an = a0
0, gdyż
an = a0 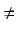 0. Dzieląc więc nasze równanie przez X0m otrzymujemy:
0. Dzieląc więc nasze równanie przez X0m otrzymujemy:
a0X0m +
a1X0m-1 +...+
am +...+
an-1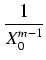
+
an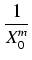
= 0.
Wobec tego, po wykonaniu niezbędnego uproszczenia powyższego wyrażenia, wykorzystując fakt, że wielomian f
jest obustronny, dostajemy:
a0fm(
X0 +
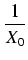
) +
a1fm-1(
X0 +
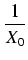
) +...+
am = 0.
Zatem liczba
Z0 = X0 + 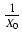 jest pierwiastkiem równania podanego w wypowiedzi twierdzenia,
zaś X0 jest pierwiastkiem równania
jest pierwiastkiem równania podanego w wypowiedzi twierdzenia,
zaś X0 jest pierwiastkiem równania
X2 - Z0X + 1 = 0.
W podobny sposób dowodzimy, że jeśli X0 jest pierwiastkiem odpowiedniego równania kwadratowego,
a Zj jest pierwiastkiem równania podanego w wypowiedzi twierdzenia, to X0 jest pierwiastkiem wyjściowego równania.
Powyższe twierdzenie orzeka zatem, że rozwiązanie równania obustronnego stopnia 2m sprowadza się
do rozwiązania równania stopnia m oraz m równań kwadratowych. Tym samym potrafimy napisać ogólne wzory
na rozwiązania równań obustronnych stopni do dziewiątego włącznie.



Next: Teoria liczb
Up: Rozwiązywanie równań
Previous: Wzory na pierwiastki dowolnego
Pawel Gladki
2006-01-30
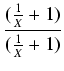 g(
g(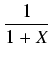 =
= 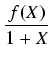 = g(X)
= g(X)
![]() 0, to pierwiastki wielomianu obustronnego:
0, to pierwiastki wielomianu obustronnego:
![]() 0, gdyż
an = a0
0, gdyż
an = a0 ![]() 0. Dzieląc więc nasze równanie przez X0m otrzymujemy:
0. Dzieląc więc nasze równanie przez X0m otrzymujemy: