Wzory na pierwiastki dowolnego wielomianu

To, że nie znamy ogólnej metody rozwiązywania równań wielomianowych przez pierwiastniki nie oznacza, że nie potrafimy podać innych metod ogólnych, przy pomocy których można wyrazić pierwiastki dowolnego wielomianu. Około 1858 roku Hermite, Kronecker i Brioschi rozwiązali równanie stopnia piątego przy pomocy modularnych całek eliptycznych. Nieco później, około roku 1870, Jordan udowadnia, że pierwiastki równania dowolnego stopnia daje się wyrazić poprzez funkcje modularne, a siedem lat później Felix Klein wyraża pierwiastki równania stopnia pięć przez funkcje hipergeometryczne. W latach 1884-1892 Lindemann podaje wzory na pierwiastki dowolnego wielomianu z użyciem funkcji $\theta$, a w 1915 roku Robert Hjalmal Mellin podaje analogiczne wzory, tym razem z wykorzystaniem tzw. całek Mellina. W latach dwudziestych XX wieku podobne rezultaty z użyciem funkcji hipergeometrycznych uzyskują Bierkeland, Capelli, Belardinelli, Pincherle, Appell i Kampe de Feriet. Podamy - za książką D. Mumforda, "Tata Lectures on Theta", Birkhäuser, Boston 1983 (t. I), 1984 (t. II) - jeden z takich rezultatów, wykorzystujący funkcję $\theta$.

Niech a₀, a₁,..., a_n będą liczbami zespolonymi, przy czym a₀ jest różne od 0 i wielomian

f (x) = a₀xⁿ + a₁x^n-1 + ... + a_n-1x + a_n

jest nierozkładalny nad ciałem $\mathbb {Q}$(a₀, a₁,..., a_n) oraz f (0), f (1) i (dla nieparzystego n) f (2) są wszystkie różne od 0. Niech $\alpha_{1}^{}$,$\alpha_{2}^{}$,...,$\alpha_{n}^{}$ będą wszystkimi zespolonymi pierwiastkami wielomianu f (x). W zależności od parzystości n rozważmy wielomian

w(x) = $$\left\{\vphantom{ \begin{array}{ll} x(x-1)(a_0 x^n + a_1 x^{n-1} ... ...{n-1} + ... + a_{n-1} x + a_n) & \mbox{ dla parzystego } n \end{array} }\right.$$$$\begin{array}{ll} x(x-1)(a_0 x^n + a_1 x^{n-1} + ... + a_{n-1} x ... ... + a_1 x^{n-1} + ... + a_{n-1} x + a_n) & \mbox{ dla parzystego } n \end{array}$$

Niech

x₁ = 0, x₂ = 1, x_i+2 = $$\alpha_{i}^{}$$

i, ewentualnie (dla parzystego n), x_n+3 = 2. Niech C będzie (zespoloną) krzywą hipereliptyczną o równaniu

y² = w(x).

Jako krzywą hipereliptyczną rozumiemy tu krzywą płaską, która w pewnym układzie współrzednych ma równanie y² = w(x), gdzie w(x) jest wielomianem rozdzielczym (tzn. bez pierwiastków wielokrotnych) stopnia większego od 4. Uwaga! Krzywa zespolona topologicznie jest powierzchnią! Zespolona (rzutowa) krzywa eliptyczna jest topologicznie równoważna z torusem (obwarzankiem z jedną dziurą), a krzywa hipereliptyczna - z "obwarzankiem" o g dziurach, gdzie

g = $$\left\{\vphantom{ \begin{array}{ll} (n-1)/2 & \mbox{ dla nieparzy... ...} n = \deg(w(x)),\\ (n-2)/2 & \mbox{ dla parzystego } n \end{array} }\right.$$$$\begin{array}{ll} (n-1)/2 & \mbox{ dla nieparzystego } n = \deg(w(x)),\\ (n-2)/2 & \mbox{ dla parzystego } n \end{array}$$

Liczbę dziur g nazywamy rodzajem krzywej.

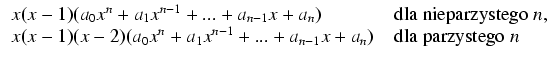
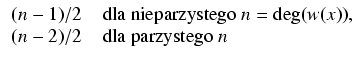
W następnej kolejności budujemy bazę grupy homologii H₁(C,$\mathbb {Z}$) krzywej zespolonej C o równaniu y² = (x - x₁) ^. ... ^. (x - x_2g+1) w taki oto sposób: Odwzorowanie p(x, y) = x przekształca krzywą C w dwulistne nakrycie prostej $\mathbb {C}$¹ (czyli płaszczyzny Gaussa), rozgałęzione w punktach x = x₁, x = x₂,..., x = x_2g+1 i w nieskończoności. Z dokładnością do równoważności topologicznej model krzywej C można zbudować, rozcinając $\mathbb {C}$¹ wzdłuż łuków łączących x₁ z x₂, x₃ z x₄, ..., x_2g-1 z x_2g, oraz x_2g+1 z punktem w nieskończoności. Następnie dwa egzemplarze takiej porozcinaniej płaszczyzny Gaussa sklejamy, łącząc ze sobą przeciwne brzegi każdego rozcięcia - ale z różnych egzemplarzy płaszczyzny Gaussa. Bazę standardową tworzy 2g konturów A₁,..., A_g, B₁,..., B_g takich, że:

• A_i obiega rozcięcie x_2i-1 - - - x_2i na pierwszym egzemplarzu płaszczyzny Gaussa,
• B_i wychodzi z nieskończoności na pierwszym egzemplarzu płaszczyzny Gaussa, przechodzi przez rozcięcie i sklejenie x_2i-1 - - - x_2i na drugi egzemplarz i wraca na nim do nieskończoności.

Baza standardowa wyznaczona jest przez kolejność pierwiastków wielomianu, wystepującego w równaniu krzywej hipereliptycznej.

Dla bazy standardowej A₁,..., A_g, B₁,..., B_g można utworzyć macierz okresów wybierając najpierw unormowaną bazę holomorficznych form różniczkowych

$$\omega_{i}^{}$$ = P_i(x)dx/y

spełniających warunki:

$$\int_{{A_i}}^{}$$$$\omega_{j}^{}$$ = $$\delta_{{ij}}^{}$$.

Macierz okresów

$$\Omega$$ = [$$\Omega_{{ij}}^{}$$]

ma elementy

$$\Omega_{{ij}}^{}$$ = $$\int_{{B_i}}^{}$$$$\omega_{j}^{}$$.

Niech zatem $\Omega$ będzie macierzą okresów krzywej C względem standardowej bazy grupy H₁(C,$\mathbb {Z}$) z numeracją zgodną z numeracją pierwiastków. Niech 2g + 1 będzie stopniem wielomianu w(x). Oznaczmy

$$\theta$$(z,$$\Omega$$) = $$\sum_{{n \in {\mathbb Z}^g}}^{}$$e^{$\pi$in$\Omega$nT+2$\pi$inzT}

jako funkcję $\theta$ wielu zmiennych oraz

$$\theta$$$$\left[\vphantom{ \begin{array}{c} a b \end{array} }\right.$$$$\begin{array}{c} a b \end{array}$$$$\left.\vphantom{ \begin{array}{c} a b \end{array} }\right]$$(z,$$\Omega$$) = e^{$\pi$ia$\Omega$a+2$\pi$ia(z+b)T}$$\theta$$(z + a$$\Omega$$ + b,$$\Omega$$)

jako funkcję $\theta$ wielu zmiennych z charakterystykami a, b.

$\theta$-funkcja wielu zmiennych $\theta$(z,$\Omega$) jest uogólnieniem klasycznej $\theta$-funkcji, funkcji analitycznej dwóch zmiennych

$$\theta$$(z,$$\tau$$) = $$\sum_{{n \in {\mathbb Z}}}^{}$$e^{$\pi$in2$\tau$+2$\pi$inz}

dla z $\in$ $\mathbb {C}$ i Im$\tau$ > 0.

Ponadto oznaczmy:

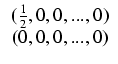
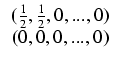
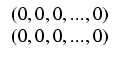
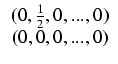
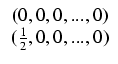
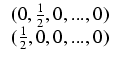
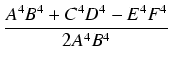A = $$\theta$$$$\left[\vphantom{ \begin{array}{c} (\frac{1}{2}, 0, 0, ..., 0) (0, 0, 0, ..., 0) \end{array} }\right.$$$$\begin{array}{c} (\frac{1}{2}, 0, 0, ..., 0) (0, 0, 0, ..., 0) \end{array}$$$$\left.\vphantom{ \begin{array}{c} (\frac{1}{2}, 0, 0, ..., 0) (0, 0, 0, ..., 0) \end{array} }\right]$$(0,$$\Omega$$),

B = $$\theta$$$$\left[\vphantom{ \begin{array}{c} (\frac{1}{2}, \frac{1}{2}, 0, ..., 0) (0, 0, 0, ..., 0) \end{array} }\right.$$$$\begin{array}{c} (\frac{1}{2}, \frac{1}{2}, 0, ..., 0) (0, 0, 0, ..., 0) \end{array}$$$$\left.\vphantom{ \begin{array}{c} (\frac{1}{2}, \frac{1}{2}, 0, ..., 0) (0, 0, 0, ..., 0) \end{array} }\right]$$(0,$$\Omega$$),

C = $$\theta$$$$\left[\vphantom{ \begin{array}{c} (0, 0, 0, ..., 0) (0, 0, 0, ..., 0) \end{array} }\right.$$$$\begin{array}{c} (0, 0, 0, ..., 0) (0, 0, 0, ..., 0) \end{array}$$$$\left.\vphantom{ \begin{array}{c} (0, 0, 0, ..., 0) (0, 0, 0, ..., 0) \end{array} }\right]$$(0,$$\Omega$$),

D = $$\theta$$$$\left[\vphantom{ \begin{array}{c} (0, \frac{1}{2}, 0, ..., 0) (0, 0, 0, ..., 0) \end{array} }\right.$$$$\begin{array}{c} (0, \frac{1}{2}, 0, ..., 0) (0, 0, 0, ..., 0) \end{array}$$$$\left.\vphantom{ \begin{array}{c} (0, \frac{1}{2}, 0, ..., 0) (0, 0, 0, ..., 0) \end{array} }\right]$$(0,$$\Omega$$),

E = $$\theta$$$$\left[\vphantom{ \begin{array}{c} (0, 0, 0, ..., 0) (\frac{1}{2}, 0, 0, ..., 0) \end{array} }\right.$$$$\begin{array}{c} (0, 0, 0, ..., 0) (\frac{1}{2}, 0, 0, ..., 0) \end{array}$$$$\left.\vphantom{ \begin{array}{c} (0, 0, 0, ..., 0) (\frac{1}{2}, 0, 0, ..., 0) \end{array} }\right]$$(0,$$\Omega$$),

F = $$\theta$$$$\left[\vphantom{ \begin{array}{c} (0, \frac{1}{2}, 0, ..., 0) (\frac{1}{2}, 0, 0, ..., 0) \end{array} }\right.$$$$\begin{array}{c} (0, \frac{1}{2}, 0, ..., 0) (\frac{1}{2}, 0, 0, ..., 0) \end{array}$$$$\left.\vphantom{ \begin{array}{c} (0, \frac{1}{2}, 0, ..., 0) (\frac{1}{2}, 0, 0, ..., 0) \end{array} }\right]$$(0,$$\Omega$$).

Wtedy zachodzi równość:

x₃ = $$\alpha_{1}^{}$$ = $${\frac{{A^4 B^4 + C^4 D^4 - E^4 F^4}}{{2 A^4 B^4}}}$$.