Co to jest wyróżnik wielomianu?

Słowo delta to nazwa czwartej litery alfabetu greckiego $\delta$, $\Delta$. Słowo delta jest również nazwą typu ujścia rzeki i typu płatowca samolotu. Natomiast - jak by się dziwne to nie wydawało, słowo delta nie jest nazwą wzoru na pierwiastki trójmianu kwadratowego ani metody obliczania tych pierwiastków. Nawet to, że wartość wyróżnika b² - 4ac trójmianu kwadratowego ax² + bx + c zwykle oznacza się literą $\Delta$ nie oznacza, że słowo delta jest nazwą wyróżnika.

Natomiast co to takiego jest wyróżnik? Rozważmy najpierw przypadek wielomianu unormowanego f (x) = xⁿ + a₁x^n-1 + ... + a_n-1x + a_n stopnia n > 1, a x₁, x₂,..., x_n są wszystkimi jego pierwiastkami (wiadomo, że istnieje ciało, w którym ten wielomian ma n pierwiastków - to znaczy, że f (x) = (x - x₁) ^. (x - x₂) ^. ... ^. (x - x_n) nawet, jeśli są pierwiastki wielokrotne), to iloczyn kwadratów różnic pierwiastków:

P_n = P_n(x₁, x₂,..., x_n) = $$\prod_{{i<j}}^{}$$(x_j - x_i)²

nie zależy od wyboru numeracji pierwiastków. Wyjaśnimy to na przykładach:

• dla n = 1 nie da się utworzyć ani jednej pary i < j, więc P₁ = 1
• dla n = 2 można utworzyć jedną różnicę x₂ - x₁, więc P₂ = (x₂ - x₁)². Jeśli oznaczyć y₁ = x₂, y₂ = x₁, to y₂, y₂ są również wszystkimi pierwiastkami wielomianu f (x) (w odwrotnej kolejności) i:
  (y₂ - y₁)² = (- (x₂ - x₁))² = (x₁ - x₂)²
  Wzory Viéte pozwalają obliczyć:
  P₂ = (x₂ - x₁)² = x₂² -2x₁x₂ + x₁² = x₁² +2x₁x₂ + x₂² -4x₁x₂ = (x₁ + x₂)² -4x₁x₂ = (- a₁)² -4a₂ = a₁² -4a₂.

• dla n = 3 można utworzyć trzy różnice: x₃ - x₂, x₃ - x₁, x₂ - x₁. Można też na sześć sposobów zmienić kolejność pierwiastków przed utworzeniem różnic. Dla każdej różnicy x_i - x_j i każdej zmiany kolejności pierwiastków są dwie możliwości: albo w nowym uporządkowaniu x_i występuje przed x_j i różnica się nie zmieniła, albo w nowym uporządkowaniu kolejność pierwiastków się odwróciła, różnica zmieniła znak na przeciwny, a kwadrat różnicy się nie zmienił. Zatem iloczyn kwadratów różnic pierwiastków pozostał niezmieniony. Użycie wzorów Viéte aby wyrazić P₃ przez współczynniki wielomianu zajmuje jednak dość dużo miejsca, więc je pomijamy.

Łatwo zauważyć, że zawsze iloczyn P_n nie zależy od kolejności pierwiastków. Wiadomo, że wyrażenie zbudowane z pierwiastków wielomianu za pomocą dodawania, odejmowania, mnożenia i stałych, które nie zależy od kolejności pierwiastków, można zapisać jako wielomian od współczynników wielomianu f (x) (jeden - "uniwersalny" - wielomian D(1, a₁,..., a_n) dla danego stopnia n). W ten sposób dotarliśmy do definicji wyróżnika: wyróżnikiem wielomianu unormowanego

f (x) = xⁿ + a₁x^n-1 + ... + a_n-1x + a_n = (x - x₁) ^. (x - x₂) ^. ... ^. (x - x_n)

stopnia n nazywamy wielomian D(f (x), x) = D(1, a₁, a₂,..., a_n) równy tożsamościowo iloczynowi

$$\prod_{{i<j}}^{}$$(x_j - x_i)²

kwadratów różnic pierwiastków tego wielomianu.

Wygodny sposób obliczania wyróżnika wykorzystuje macierz Vandermonde'a

V_n(x₁, x₂,..., x_n) = $$\left[\vphantom{ \begin{array}{ccccc} 1 & 1 & 1 & \ldots & 1 ... ... x_1^{n-1} & x_2^{n-1} & x_3^{n-1} & \ldots & x_n^{n-1} \end{array} }\right.$$$$\begin{array}{ccccc} 1 & 1 & 1 & \ldots & 1 \\ x_1 & x_2 & x_3... ...\vdots \\ x_1^{n-1} & x_2^{n-1} & x_3^{n-1} & \ldots & x_n^{n-1} \end{array}$$$$\left.\vphantom{ \begin{array}{ccccc} 1 & 1 & 1 & \ldots & 1 ... ... x_1^{n-1} & x_2^{n-1} & x_3^{n-1} & \ldots & x_n^{n-1} \end{array} }\right]$$

i jej wyznacznik, zwany wyznacznikiem Vandermonde'a (A. Mostowski, M. Stark, Elementy algebry wyższej, IV 4.3):

det V_n(x₁, x₂,..., x_n) = $$\prod_{{i<j}}^{}$$(x_j - x_i).

Jak widać,

Pn = (det V_n)² = det(V_n×V_n^T) = det[s_ij]

gdzie

s_ij = x₁^i+j-2 + x₂^i+j-2 + ... + x_n^i+j-2.

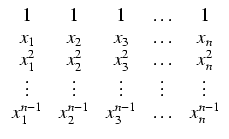
Sumy potęg pierwiastków wielomianu można wyrazić przez współczynniki tego wielomianu za pomocą wzorów Newtona.

Z definicji dla danego wielomianu f (x) jego wyróżnik jest równy zero wtedy i tylko wtedy, gdy ten wielomian ma pierwiastki wielokrotne. Dla każdej stałej t wielomian g(x) = f (x + t) uzyskany z f (x) przez podstawienie x + t za x ma ten sam wyróżnik, co wielomian f (x). Z tego, że zerowanie się wyróżnika jest równoważne temu, że wielomian ma pierwiastki wielokrotne, wynika, że wyróżnik jest - z dokładnością do znaku - rugownikiem wielomianu i jego pochodnej (A. Mostowski, M. Stark, Elementy algebry wyższej, X):

D(f (x), x) = (- 1)^n(n-1)/2R(f (x), f'(x)).

Wyróżnik wielomianu unormowanego f (x) stopnia n jest wielomianem stopnia 2n - 2 od współczynników wielomianu f (x). Ten wielomian D(1, a₁, a₂,..., a_n) ma całkowite współczynniki.

Przejdźmy teraz do definicji wyróżnika dla dowolnego wielomianu. Wyróżnikiem D(f (x), x) wielomianu

f (x) = a₀xⁿ + a₁x^n-1 + ... + a_n-1x + a_n = a₀(x - x₁)(x - x₂)...(x - x_n)

stopnia n nazywamy iloczyn a₀^2n-2 i wyróżnika wielomianu unormowanego proporcjonalnego do f (x)

D(f (x), x) = a₀^2n-2D($${\frac{{1}}{{a_0}}}$$f (x), x)

D(a0, a1, a2,..., an) = a₀^2n-2D(1,$${\frac{{a_1}}{{a_0}}}$$,...,$${\frac{{a_n}}{{a_0}}}$$)

Wyróżnik wielomianu jest wielomianem jednorodnym stopnia 2n - 2 od współczynników danego wielomianu. Ten wielomian D(a₀, a₁, a₂,..., a_n) ma całkowite współczynniki i jest wielomianem izobarycznym stopnia n(n - 1), tzn. jest on sumą jednomianów

t ^. a₀^{k(0) .} a₁^{k(1) .} a₂^{k(2) .} ... ^. a_n^k(n)

i dla każdego z nich

k(0) + k(1) + k(2) + ... + k(n) = 2n - 2

0 ^. k(0) + 1 ^. k(1) + 2 ^. k(2) + ... + n ^. k(n) = n(n - 1).

Jednorodność oznacza, że

D(tf (x), x) = t^2n-2D(f (x), x),

a izobaryczność - że

D(tⁿf ($${\frac{{x}}{{t}}}$$), x) = t^n(n-1)D(f (x), x).

Wyróżnik wielomianu wyraża się przez rugownik wielomianu i jego pochodnej:

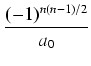D(f (x), x) = $${\frac{{(-1)^{n(n - 1)/2}}}{{a_0}}}$$R(f (x), f'(x))

Z własności rugownika pary wielomianów wynikają wzory:

• D(f (x), x) = (- 1)^n(n-1)/2a₀^n-2$\prod_{{i=1}}^{n}$f'(x_i), gdzie x₁, x₂,..., x_n są wszystkimi pierwiastkami wielomianu f (x);
• D(f (x), x) = (- 1)^n(n-1)/2nⁿa₀^n-1$\prod_{{i=1}}^{{n-1}}$f (y_i), gdzie y₁, y₂,..., y_n-1 są wszystkimi pierwiastkami pochodnej f'(x) wielomianu f (x);
• D(f (x)g(x), x) = D(f (x), x) ^. D(g(x), x)R(f (x), g(x))².

Korzystając z wzoru z iloczynem wartości pochodnej w pierwiastkach wielomianu i paru sztuczek, łatwo wyprowadzić wzór na wyróżnik trójmianu dowolnego stopnia:

D(xⁿ + px + q, x) = (- 1)^n(n-1)/2(nⁿq^n-1 + (1 - n)^n-1pⁿ)

Kilka przykładów:

• D(ax² + bx + c, x) = b² - 4ac.
• D(ax³ + bx² + cx + d, x) = 18abcd - 4ac³ +27a²d² + b²c² -4b³d.
• D(x³ + px + q, x) = - 4p³ -27q².
• 
  

  = 256a³e³ -192a²bde² -128a²c²e² +144a²cd²e

  - 27a²d⁴ +144ab²ce² -6ab²d²e - 80abc²de

  + 18abcd³ +16ac⁴e - 4ac³d² -27b⁴e² -4b³d³

  - 4b²c³e + b²c²d² +18b³cde.

  
  
• D(x⁴ + px² + qx + r, x) = - 4p³q² -27q⁴ +16p⁴r - 128p²r² +144pq²r + 256r³.
• 
  

  = 2000pr²s² -900p³rs² +144pq²r³

  + 16p⁴r³ -128p²r⁴ +256r⁵

  + 3125s⁴ +108p⁵s² +825p²q²s²

  - 4p³q²r² +16p³q³s - 3750pqs³

  + 560p²qr²s - 72p⁴qrs - 630pq³rs

  + 2250q²rs² -1600qr³s - 27q⁴r²

  + 108q⁵s

  
  

W teorii Galois rozszerzenie o pierwiastek kwadratowy z wyróżnika odpowiada podgrupie alternującej A_n grupy symetrycznej S_n, która jest grupą Galois wielomianu ogólnego stopnia n.