Rozważmy model przepływu krwi w naczyniu krwionośnym, takim jak żyła lub tętnica. Możemy przyjąć, że naczynie krwionośne ma kształt cylindrycznej rury o promieniu zewnętrznym R, promieniu wewnętrznym r, a następnie rozważyć odcinek naczynia o długości l. Z uwagi na lepkość krwi i opór stawiany podczas przepływu, prędkość przepływu krwi v jest największa blisko osi symetrii naczynia i zmniejsza się wraz ze zmniejszaniem się odległości r od ścianek naczynia, aby ostatecznie osiągnąć wartość zero. Związek między prędkością przepływu v i odległością od ściany naczynia r opisuje prawo przepływu krwi odkryte doświadczalnie przez francuskiego lekarza Jean'a-Louis'a-Marie Poiseuille'a w 1840 roku:
Chcąc teraz obliczyć ilość krwi przepływającej przez naczynię (ilość rozumiemy tu jako stosunek objętości do jednostki czasu), podzielmy przekrój naczynia za pomocą koncentrycznych okręgów o promieniach r1, r2,..., rn takich, że różnica pomiędzy kolejnymi dwoma promieniami jest stała. Pole powierzchni pierścienia wyznaczonego przez dwa sąsiadujące okręgi równa jest więc
![\includegraphics[width=12cm]{572-4.eps}](img896.gif)
Jeśli ![]() r jest odpowiednio małe, to prędkość przepływu jest w przybliżeniu stała na całej powierzchni
pierścienia i może być przybliżona przez wartość v(ri). Wobec tego objętość krwi przepływająca w jednostce
czasu równa jest w przybliżeniu
r jest odpowiednio małe, to prędkość przepływu jest w przybliżeniu stała na całej powierzchni
pierścienia i może być przybliżona przez wartość v(ri). Wobec tego objętość krwi przepływająca w jednostce
czasu równa jest w przybliżeniu
![\includegraphics[width=12cm]{573-5.eps}](img897.gif)
Oczywiście prędkość przepływu (a więc i ilość przepływającej krwi) jest tym większa, im bliżej osi symetrii
naczynia się znajdujemy. Przybliżenie otrzymane w powyższych obliczeniach będzie tym dokładniejsze,
im większe n przyjmiemy do obliczeń - nietrudno zatem zauważyć, że całkowita ilość przepływającej krwi
wyrazi się wzorem
| F | = | ||
| = | |||
| = | 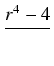 ]|r=0r=R = ]|r=0r=R = |
||
| = | 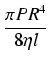 . . |
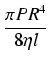
Zagadnieniem pokrewnym jest obliczanie wydajności serca, czyli ilości krwi F
(rozumianej jako stosunek objętości do jednostki czasu) pompowanej przez serce do aorty. Metoda mierzenia
wydajności serca jest następująca: do prawej komory serca wstrzykuje się kontrast, który razem z krwią
przepompowywany jest przez serce do aorty. Sonda umieszczona w aorcie mierzy stężenie kontrastu w krwi
opuszczającej serce w równych odstępach czasu w pewnym przedziale czasowym [0, T], dopóki kontrast przestaje
być wykrywalny. Niech c(t) oznacza stężenie kontrastu w krwi w momencie t. Jeśli podzielimy przedział
[0, T] na małe podprzedziały o równej długości ![]() t, wyznaczone przez momenty
t1, t2,..., tn, to ilość kontrastu przepływającego w ciągu podprzedziału
[ti-1, ti] równa
jest w przybliżeniu
t, wyznaczone przez momenty
t1, t2,..., tn, to ilość kontrastu przepływającego w ciągu podprzedziału
[ti-1, ti] równa
jest w przybliżeniu
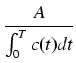 .
.