Wielkie twierdzenie Fermata

Zadanie 8 z drugiej księgi "Arytmetyki" Diofantosa ma następującą treść:

"Dany kwadrat rozłożyć na [sumę] dwa kwadraty."

Rozwiązanie ilustruje wzór a² = (${\frac{{2ak}}{{k^2 +1}}}$)² + (${\frac{{a(k^2 -1)}}{{k^2 +1}}}$)² (k dowolne) na przykładzie a = 4, k = 2 (Diofantosa interesowało rozwiązywanie równań w liczbach wymiernych; dziś równania diofantyczne rozwiązuje się w liczbach całkowitych).

W 1464 Regimontanus (Johannes Miller, 16 VI 1436 - 6 VII 1476), zamiłowany zbieracz i tłumacz greckich manuskryptów, odnalazł w Wenecji Arytmetykę Diofantosa. W 1575 po raz pierwszy Xilander wydał łaciński przekład Arytmetyki Diofantosa. Simon Stevin przetłumaczył ją na francuski. W 1621 roku G. C. Bachet de Meziriac wydał grecką i łacińską wersję sześciu znanych (z trzynastu napisanych) rozdziałów (ksiąg) Arytmetyki Diofantosa z komentarzami i uzupełnieniami.

Po śmierci Fermata na marginesie jego egzemplarza książki w tym właśnie miejscu znaleziono dopisek treści:

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.

co w tłumaczeniu oznacza:

Przeciwnie, nie można rozłożyć ani sześcianu na [sumę] dwa sześciany, ani bikwadratu na [sumę] dwa bikwadraty, i w ogóle żadnej potęgi większej niż druga na [sumę] dwie potęgi z takim samym wykładnikiem. Odkryłem naprawdę zadziwiający dowód tego [faktu]. Margines jest na to za mały.

Przypuszcza się, że dopisek pojawił się na marginesie w 1630 roku; jeśli to prawda, to z faktu, że Fermat nigdy więcej o tym "naprawdę zadziwiającym dowodzie" nie wspominał, wynikałoby, że znalazł w nim błąd. Teraz to twierdzenie formułuje się tak:

Twierdzenie: Jeśli n > 2, to równanie

Xⁿ + Yⁿ = Zⁿ

nie ma rozwiązań w liczbach naturalnych X, Y, Z.

i nazywa Wielkim Twierdzeniem Fermata (po angielsku z reguły nazywa się je Fermat Last Theorem i oznacza skrótem FLT). Zdanie "Dla danego wykładnika n równanie Xⁿ + Yⁿ = Zⁿ nie ma rozwiązań w liczbach naturalnych X < Y, Z" nazywamy Wielkim Twierdzeniem Fermata dla wykładnika n.

Warto w tym miejscu wspomnieć o autorze tego twierdzenia, które fascynowało matematyczny świat przez trzy stulecia. Pierre Fermat, francuski prawnik i matematyk-amator urodził się 17 siepnia 1601 a umarł 12 stycznia 1665. Największym jego sukcesem jako prawnika było miejsce w parlamencie Tuluzy; jako matematyk zdobył wieczną sławę:

• wraz z Kartezjuszem stworzył geometrię analityczną - jako pierwszy wprowadził prostokątny układ współrzędnych;
• był pionierem rachunku różniczkowego (znajdowanie ekstremów i stycznych, wzory na pochodną i całkę nieoznaczoną funkcji potęgowej z wymiernym wykładnikiem),
• wniósł wkład w rozwój rachunku prawdopodobieństwa;
• zbudował optykę geometryczną na zasadzie wariacyjnej (zasada najkrótszego czasu).

W dziedzinie teorii liczb Fermat:

• podał metodę rozkładania dużych liczb na czynniki pierwsze,
• znalazł metodę rozwiązywania równania diofantycznego ax² +1 = y² (wskutek pomyłki zwanego równaniem Pella),
• sformułował twierdzenie o przedstawialności liczb naturalnych jako sum czterech kwadratów,
• ogłosił, że udowodnił twierdzenie (zwane twierdzeniem Girarda), charakteryzujące liczby naturalne, które są sumami dwóch kwadratów,
• odkrył twierdzenia charakteryzujące liczby, które dają się przedstawić w postaci x² +2y² i x² +3y²,
• określił liczby Fermata F_n = 2^N + 1, N = 2ⁿ, wyrażając przypuszczenie (błędne) że są one wszystkie liczbami pierwszymi,
• udowodnił tzw. Małe Twierdzenie Fermata : jeśli p jest liczbą pierwszą i a jest liczbą całkowitą niepodzielną przez p, to liczba a^p-1 - 1 dzieli się przez p,
• udowodnił, że równania x⁴ + y⁴ = z² i x⁴ - y⁴ = z² nie mają rozwiązań w liczbach naturalnych x, y, z stosując jako pierwszy jedną z wersji zasady indukcji - zasadę regresji.

Prawie cały dorobek matematyczny Fermata ukazał się po jego śmierci, wydany przez jego syna jako "Varia opera mathematica", Tolosae 1679. Za życia swoje osiągnięcia matematyczne Fermat umieszczał w prywatnej korespondencji z innymi uczonymi.

* * *

W niniejszej nocie poza standardowymi oznaczeniami $\mathbb {Z}$, $\mathbb {Q}$, $\mathbb {R}$, $\mathbb {C}$, $\mathbb {F}$_p dla liczb całkowitych, wymiernych, rzeczywistych, zespolonych i ciała reszt modulo p, przyjmiemy także oznaczenie $\mathbb {A}$ dla ciała liczb algebraicznych, $\mathbb {Q}$_p dla ciała liczb p-adycznych, $\mathbb {Z}$_p dla pierścienia liczb całkowitych p-adycznych i $\zeta_{n}^{}$ dla n-tego pierwiastka pierowtnego z jedynki.

* * *

Jest jasne, że ze słuszności FLT dla pewnego wykładnika n wynika jego prawdziwość dla wszystkich wielokrotności n. Ponieważ każda liczba naturalna większa od jedności i nie będąca potęgą dwójki ma nieparzysty dzielnik pierwszy, wystarczy udowodnić twierdzenie dla wszelkich n będących liczbami pierwszymi nieparzystymi i dla n = 4. W tym ostatnim przypadku dowód został podany już przez Fermata - po śmierci matematyka jego notatki zostały wydane przez syna, w szczególności notki na marginesie ukazały się drukiem około roku 1670 (P. Fermat, Observationes Domini Petri de Fermat, Oeuvres, I, 289 - 342, Paris 1891). W swoim dowodzie Fermat zastosował swoją "metodę spadku", wykorzystując znany już wówczas opis wszystkich rozwiązań równania pitagorejskiego:

X² + Y² = Z²

w liczbach całkowitych: jeśli liczby X, Y, Z spełniają powyższe równanie, X, Y są względnie pierwsze, a Y jest nieparzysta, to istnieją względnie pierwsze liczby całkowite u, v takie, że X = 2uv, Y = u² - v² oraz Z = u² + v². Fermat w istocie udowodnił trochę inne twierdzenie, dowodząc nieistnienia trójkąta prostokątnego o całkowitych bokach i polu będącym kwadratem liczby naturalnej, ale po drodze jego rozumowanie daje następujący rezultat:

Twierdzenie: Równanie X⁴ + Y⁴ = Z² nie ma rozwiązań naturalnych.

Dowód: Załóżmy, że równanie

(X²)² + (Y²)² = X⁴ + Y⁴ = Z²

ma rozwiązanie naturalne i przyjmijmy, że Z > 0 jest minimalne. Bez straty ogólności możemy założyć, że X jest liczbą parzystą, a Y nieparzystą. Z opisu rozwiązań równania Pitagorasa wynika istnienie względnie pierwszych liczb naturalnych u > v takich, że X² = 2uv, Y² = u² - v² oraz Z = u² + v². Nietrudno spostrzec, że v musi być parzyste, a ponieważ u² = Y² + v², więc powtarzając poprzednie rozumowanie otrzymujemy istnienie względnie pierwszych liczb całkowitych a, b, spełniających v = 2ab, Y = a² - b² i u = a² + b². To daje:

X² = 2uv = 4ab(a² + b²),

skąd wynika, że liczby a, b, a² + b² są kwadratami, ponieważ są względnie pierwsze:

a = x²,    b = y²,    a^b + b² = z².

Ostatecznie:

x⁴ + y⁴ = z²

co stoi w sprzeczności z minimalnością Z, mamy bowiem 0 < z < Z.

Z uwagi na powyższe twierdzenie będziemy sie w dalszym ciągu zajmować równaniem

X^p + Y^p = Z^p

gdzie p jest nieparzystą liczbą pierwszą. Jako że (- 1)^p = - 1, równanie to wygodniej będzie zapisywać jako:

X^p + Y^p + Z^p = 0,

przy czym możemy dodatkowo założyć, że liczby X, Y, Z nie mają wspólnego dzielnika właściwego, w przeciwnym bowiem razie moglibyśmy podzielić obydwie strony równania przez p-tą potęgę tego dzielnika. Tradycyjnie rozróżnia się tu dwa przypadki:

• Pierwszy przypadek FLT: żadna z liczb X, Y, Z nie dzieli się przez p
• Drugi przypadek FLT: p nie dzieli XYZ.

* * *

W 1729 Ch. Goldbach w liście do mającego wówczas 22 lata Leonharda Eulera wspomniał o licznych hipotezach, zawartych w opublikowanych notatkach. W ten sposób zainteresował Eulera teorią liczb. Trzy lata później Euler pierwszą pracę z teorii liczb - obalił hipotezę Fermata o tym, że tzw. liczby Fermata są pierwsze. W 1770 roku ukazał się "Wstęp do algebry" Eulera (L. Euler, "Vollständige Anleitung in die Algebra", St. Petersburg 1770, przedruk: "Opera omnia I.1", Teubner 1911), zawierający w paragrafie 242 dowód FLT w przypadku n = 3. Euler korzystał w nim z pewnych własności arytmetycznych formy kwadratowej x² +3y², nie podając ich uzasadnienia, tak więc przez długi czas uważano, że dowód ten jest niekompletny. Dopiero w ostatnich latach spostrzeżono (por. G. Bergmann, "Über Euler's Beweis des grossen Fermatschen Satzes für den Exponenten 3", Math. Ann. 164 (1966), 159 - 175) że brakujące uzasadnienie wynika bez trudu z jednej z wcześniejszych prac Eulera z 1760 roku. W 1800 roku Gauss udowodnił jednoznaczność rozkładu w pierścieniu $\mathbb {Z}$[$\zeta_{3}^{}$], z której prosto wynika dowód FLT dla wykładnika 3. Podamy wersję tego dowodu w oparciu o pracę Mann'a i Webb'a z 1978 roku.

Twierdzenie: W przypadku n = 3 równanie

Xⁿ + Yⁿ = Zⁿ

nie ma rozwiązań całkowitych.

Dowód: Niech liczby x, y, z będą całkowitymi rozwiązaniami naszego równania - możemy je przy tym wybrać w ten sposób, że liczba | xyz| > 0 jest możliwie najmniejsza. Wówczas liczby te są parami względnie pierwsze. Gdyby żadna z nich nie dzieliła się przez 3, to ich trzecie potęgi dawałyby reszty 1 lub 8 z dzielenia przez 9, a zatem mielibyśmy

x³ + y³ $$\nequiv$$ z³(mod9).

Możemy zatem bez straty ogólności założyć, że z dzieli się przez 3 oraz x $\equiv$ 1(mod3) i y $\equiv$ 2(mod3). Wówczas z³ $\equiv$ 0(mod27) i z uwagi na z³ = x³ + y³ = (x + y)(x² - xy + y²) oraz NWD(x + y, x² - xy + y²) = 3 otrzymujemy x + y = 9a³ oraz x² - xy + y² = 2b³ przy odpowiednio dobranych całkowitych a, b, gdzie 1$\nmid$b.

Teraz skorzystamy z kilku prostych własności pierścienia:

R = {u + v$$\zeta_{3}^{}$$ : u, v $$\in$$ $$\mathbb {Z}$$}.

Jest to pierścień z jednoznacznością rozkładu, a jego jedynymi elementami odwracalnymi są liczby $\pm$1, $\pm$$\zeta_{3}^{}$ i $\pm$$\zeta_{3}^{2}$. W R mamy następujący rozkład:

x² - xy + y² = (x + $$\zeta_{3}^{}$$y)(x + $$\zeta_{3}^{2}$$y),

a z uwagi na NWD(x + $\zeta_{3}^{}$y, x + $\zeta_{3}^{2}$y) = 1 - $\zeta_{3}^{}$ oraz (1 - $\zeta_{3}^{}$)² = - 3$\zeta_{3}^{}$ dostajemy:

x + $$\zeta_{3}^{}$$y = $$\alpha$$(1 - $$\zeta_{3}^{}$$)(u + v$$\zeta_{3}^{}$$)³,

gdzie $\alpha$ $\in$ R jest odwracalny, zaś u, v $\in$ $\mathbb {Z}$. Dzieląc przez 1 - $\zeta_{3}^{}$ otrzymujemy:

$$\alpha$$(u + v$$\zeta_{3}^{}$$)³ = c + 3a³$$\zeta_{3}^{}$$,

przy czym c = ${\frac{{1}}{{3}}}$(2x - y) jest liczbą całkowitą, nie dzielącą się przez 3. Stąd $\alpha$(u³ + v³) $\equiv$ c(mod3), a zatem $\alpha$ przystaje do pewnej liczby całkowitej wymiernej według modułu 3. Bezpośredni rachunek pozwala sprawdzić, że jest to możliwe tylko dla $\alpha$ = 1 i $\alpha$ = - 1. Zmieniając w razie konieczności znaki u i v możemy założyć, że $\alpha$ = 1. Wobec tego:

c + 3a³$$\zeta_{3}^{}$$ = u³ -3uv² + v³ + (3u²v - 3uv²)$$\zeta_{3}^{}$$,

a więc a³ = uv(u - v). Liczby u, v, u - v są parami względnie pierwsze, co daje ostatecznie u = k³, v = l³ oraz u - v = m³; widzimy więc, że k, l, m spełniają l³ + m³ = k³, co wobec 0 < | klm| < | xyz| daje sprzeczność.

* * *

W następnych latach dowodzono FLT dla poszczególnych małych wykładników. I tak, w roku 1816 Akademia Francuska ufundowała nagrodę za pracę o FLT. W latach 20-tych XIX wieku Sophie Germaine opublikowała dowód twierdzenia: jeśli p i 2p + 1 są liczbami pierwszymi, to równanie x^p + y^p = z^p nie ma rozwiązań takich, że p nie dzieli xyz (zachodzi I przypadek FLT). Wielkie Twierdzenie Fermata dla wykładnika 5 udowodnili w 1825 P.G. Lejeune-Dirichlet i A. M. Legendre, zaś w 1832 Dirichlet udowonił FLT dla wykładnika 14. Twierdzenie dla wykładnika 7 udowodnił w 1839 G. Lamé. 1 marca 1847 roku zaczęło się długie współzawodnictwo między Lamé i A. L. Cauchy o pierwszeństwo dowodu Wielkiego Twierdzenia Fermata z wykorzystaniem arytmetyki pierścienia $\mathbb {Z}$[$\zeta_{n}^{}$]. Żadnemu ze współzawodników nie udało się udowodnić, że w tym pierścieniu zachodzi jednoznaczność rozkładu na czynniki pierwsze. 15 marca P. L. Wantzel ogłosił, że udało mu się to wykazać, ale jego dwód obejmował tylko przypadki n = 2, 3i4 (tzn. pierścienie $\mathbb {Z}$, $\mathbb {Z}$[${\frac{{1+\sqrt{-3}}}{{2}}}$]) i $\mathbb {Z}$[i]). 22 maja 1847 J. Liouville opublikował list, który otrzymał z Wrocławia od E. Kummera: Kummer relacjonował swój artykuł sprzed trzech lat, w którym wykazał, że w pierścieniu $\mathbb {Z}$[$\zeta_{n}^{}$] ogólnie rzecz biorąc nie zachodzi jednoznaczność rozkładu na czynniki pierwsze. W tym samym liście Kummer zaproponował wykorzystanie rozkładu w pierścieniu $\mathbb {Z}$[$\zeta_{n}^{}$] nie na czynniki nierozkładalne, ale na tzw. dzielniki idealne. Był to znaczący krok naprzód.

Aby przybliżyć teorię stworzonych przez Kummera liczb idealnych musimy najpierw zdefiniować liczby pierwsze regularne. Używając terminologii algebraicznej teorii liczb można najprościej powiedzieć, że liczba pierwsza p jest regularna jeżeli liczba klas ideałów pierścienia $\mathbb {Z}$[$\zeta_{p}^{}$] nie dzieli się przez p. Mamy tu na myśli klasy równoważności następującej relacji: mówimy, że ideały I, J w pierścieniu przemiennym R są równoważne, jeśli istnieją niezerowe elementy $\alpha$,$\beta$ $\in$ R spełniające $\alpha$I = $\beta$J.

Klasyczna definicja liczb pierwszych regularnych wykorzystuje pojęcie liczb Bernoulliego: liczba pierwsza p jest regularna, jeśli licznik żadnej z liczb B₂, B₄,..., B_p-3 nie dzieli się przez p. Przypomnijmy, że liczby Bernoulliego B_n są zdefiniowane następująco:

$${\frac{{z}}{{e^z - 1}}}$$ = $$\sum_{{n=0}}^{{\infty}}$$$${\frac{{B_n}}{{n!}}}$$zⁿ.

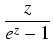Jeszcze inna definicja liczb pierwszych regularnych jest zupełnie elementarna: liczba pierwsza p jest regularna, jeżeli dla k = 1, 2,...,${\frac{{p-3}}{{2}}}$ suma

1 + 2^2k +3^2k +...+ (p - 1)^2k

nie dzieli się przez p².

Można sprawdzić - co uczynił już Kummer - że wśród liczb pierwszych mniejszych od 100 jedynie 37, 59 i 67 nie są regularne. W rzeczy samej, 67 dzieli licznik liczby B₅₈ równy

844836133488004186204675994036021,

59 dzieli licznik liczby B₄₄ równy

27833269579301024235023,

a 37 dzieli licznik B₃₂ równy

7709321041217.

W 1850 roku Kummer udowodnił następujące:

Twierdzenie: Jeśli liczba pierwsza p > 2 jest regularna, to FLT jest prawdziwe dla wykładnika p.

W 1857 roku Kummer zastosował swoją metodę do dowodu FLT dla niektórych liczb pierwszych nieregularnych, w szczególności dla p = 37, 59, 67, dowodząc tym samym FLT dla wszystkich wykładników pierwszych mniejszych od 100. Dowód ten miał pewne luki, które zostały uzupełnione w 1926 roku przez Vandivera.

W latach 80 XX wieku, dzięki rozwojowi komputerów, udało się zastosować metody Kummera i pewne ich wzmocnienia dla potwierdzenia FLT dla wykładników pierwszych mniejszych od czterech milionów. Nie wiadomo, czy istnieje nieskończenie wiele regularnych liczb pierwszych; wiadomo, że istnieje nieskończenie wiele nieregularnych liczb pierwszych (Jensen, 1915). Teoria idealnych dzielników Kummera rozwinęła się w dwie teorie: teorię ideałów i teorię dywizorów.

Około 1850 roku Francuska Akademia Nauk ufundowała drugą nagrodę, w wysokości 3 000 franków, za udowodnienie Wielkiego Twierdzenia Fermata. Nagrodę wycofano, a potem przyznano ją Kummerowi w 1857 roku. 50 lat później, w 1908 roku, miłośnik matematyki Wolfskehl zapisał w testamencie 100 000 marek temu, kto udowodni lub obali FLT. Setki tysięcy ludzi zaczęły bombardować towarzystwa i czasopisma naukowe rękopisami, zawierającymi "dowody" Wielkiego Twierdzenia Fermata. Samo Towarzystwo Matematyczne w Getyndze w ciągu trzech lat od ogłoszenia testamentu Wolfskehla otrzymało ponad tysiąc "dowodów". To, że zapisana suma straciła całkiem wartość wskutek inflacji po pierwszej wojnie światowej zmniejszyło ilość próbujących szczęścia, ale nie ugasiło emocji, które Wielkie Twierdzenie Fermata budzi do dziś.

W Polsce ostatnia afera, rozpętana przez dziennikarzy wokół szaleńca (nazywał się Zajączkowski), który odwiedzał matematyków oświadczając, że ma - złożony u notariusza - dowód Wielkiego Twierdzenia Fermata, ale nikomu go nie zdradzi i oburzał się, kiedy odpowiadano mu "Do widzenia", miała miejsce w 1975 roku. Obecnie, już po podaniu dowodu FLT przez Wilesa, śrenio raz na miesiąc na grupach dyskusyjnych pojawiają się kolejne "dowody" twierdzenia.

* * *

Kolejny krok naprzód został wykonany w 1909 roku przez Wiefericha. Udowodnił on, że jeśli I przypadek FLT jest fałszywy dla wykładnika p, to wtedy

2^p-1 $$\equiv$$ 1(modp²).

Znane są tylko dwie liczby pierwsze p spełniające powyższą kongruencję, a mianowicie 1093 i 3511. Lehmer sprawdził w 1984, że nie ma innych w przedziale [3512;6 ^. 10⁹]. W tym samym roku 1909 Mirimanoff pokazał, że jeśli FLT jest fałszywe w pierwszym przypadku dla wykładnika p, to wówczas nie tylko

2^p-1 $$\equiv$$ 1(modp²),

ale również

3^p-1 $$\equiv$$ 1(modp²).

Nie wiemy, czy istnieje choć jedna liczba pierwsza spełniająca jednocześnie obydwie powyższe kongruencje. Najlepsze wzmocnienie tego wyniku uzyskali w 1988 roku Granville i Monagan, którzy sprawdzili, że jeśli FLT jest fałszywe w I przypadku, to dla wszystkich liczb pierwszych q $\leq$ 89 musi być:

q^p-1 $$\equiv$$ 1(modp²).

Rezultat ten pozwolił potwierdzić FLT dla wszystkich wykładników pierwszych p < 7568 ^. 10¹⁷ (Coppersmith, 1990).

* * *

Warto tu wspomnieć także o innych rezulatach jakościowych. W 1953 Inkeri udowodnił, że jeśli X^p + Y^p = Z^p i X < Y < Z, to

• w I przypadku x > (${\frac{{2p^3+p}}{/}}$log 3p)^p;
• w II przypadku x > p^3p-4.

W 1971 Brillhart, Tonascia i Weinberger udowodnili - stosując powyższe twierdzenie oraz jego wzmocnienia - że I przypadek WTF zachodzi dla wszystkich wykładników pierwszych mniejszych od 3 ^. 10⁹.

* * *

Dalszy postęp w pierwszym przypadku FLT uzyskali w 1985 roku - na polu "arytmetycznym" - Adleman i Heath-Brown, którzy udowodnili prawdziwość FLT dla nieskończenie wielu wykładników pierwszych pewnej szczególnej postaci. Ich metoda była rozwinięciem idei, u których źródła leży następujące elementarne twierdzenie Sophie Germain z 1823 roku:

Twierdzenie: Jeśli p i q = 2p + 1 są liczbami pierwszymi, to dla wykładnika p FLT jest prawdziwe w pierwszym przypadku.

Twierdzenie to zostało wzmocnione przez Legendre'a w tym samym 1823 roku: okazuje się, że liczbę q = 2p + 1 można zastąpić przez q = 2kp + 1 dla k = 1, 2, 4, 5, 7, 8. Opierając się na pomyśle Wendta z 1894 roku Adleman i Heath-Brown pokazali, że jeśli k nie dzieli się przez 3, pierwszy przypadek FLT jest fałszywy dla wykładnika p oraz 2kp + 1 jest liczbą pierwszą, to p należy do pewnego skończonego zbioru T_k, mającego co najwyżej ck² elementów, gdzie c oznacza pewną stałą.

Niech A oznacza zbiór wszystkich liczb pierwszych, dla których FLT jest fałszywe w pierwszym przypadku. Wynik Adlemana i Heath-Browna natychmiast pociąga, że dla dowolnych liczb y < x liczba par:

{(p, q) : p $$\in$$ A $$\cap$$ (y, x] $$\wedge$$ q = 2kp + 1 $$\wedge$$ 3$$\nmid$$k}

nie przekracza c₁(${\frac{{x}}{{y}}}$)³ dla pewnej stałej c₁. W tym samym 1985 roku Fouvry pokazał, że dla y = x^$\vartheta$ przy pewnym $\vartheta$ > ${\frac{{2}}{{3}}}$ liczba N_$\vartheta$(x) takich par, przy opuszczeniu warunku p $\in$ A spełnia

N_$\vartheta$(x) $$\geq$$ c₂$${\frac{{x}}{{\log x}}}$$,

gdzie c₂ > 0 jest pewną stałą. Tym samym otrzymujemy istnienie pewnej liczby pierwszej p > x^$\vartheta$ nie należącej do A. Wobec dowolności x daje to nieskończenie wiele liczb pierwszych, dla których FLT jest prawdziwe w pierwszym przypadku.

* * *

Na tym etapie odejdziemy od referowania dalszych "arytmetycznych" rezultatów związanych z FLT, a skupimy się na aspekcie "geometrycznym". Twierdzenie Fermata zostało udowodnione metodami nowoczesnej geometrii algebraicznej - i teraz skupimy się na opisie kluczowych metod użytych w dowodzie. Pierwszym i zarazem milowym krokiem było udowodnienie w 1983 roku przez Gerda Faltingsa hipotezy Mordella, z której natychmiast wypływa następujący wniosek:

Twierdzenie: Dla każdej ustalonej liczby naturalnej n $\geq$ 4 równanie Fermata może mieć jedynie skończenie wiele względnie pierwszych rozwiązań całkowitych X, Y.

Twierdzenie to zgrabniej wypowiedzieć w języku geometrycznym:

Twierdzenie: Na krzywej o równaniu Xⁿ + Yⁿ = 1 może leżeć co najwyżej skończenie wiele punktów o współrzędnych wymiernych.

lub jeszcze inaczej:

Twierdzenie: Na krzywej o równaniu Xⁿ + Yⁿ + Zⁿ = 0 na płaszczyźnie rzutowej może leżeć co najwyżej skończenie wiele punktów o współrzędnych wymiernych.

O czym mówi hipoteza Mordella? Potrzebne nam będzie najpierw pojęcie rodzaju krzywej algebraicznej. Ograniczymy się przy tym do krzywych bez punktów osobliwych. Niech zatem $\Gamma$ będzie krzywą na zespolonej płaszczyźnie rzutowej daną równaniem f (X, Y, Z) = 0, przy czym f jest jednorodnym wielomianem trzech zmiennych o zespolonych współczynnikach. Punkt P = (x, y, z) $\in$ $\Gamma$ nazywamy punktem osobliwym, jeżeli:

$${\frac{{\partial f}}{{\partial x}}}$$(P) = $${\frac{{\partial f}}{{\partial y}}}$$(P) = $${\frac{{\partial f}}{{\partial z}}}$$(P) = 0.

Jeśli założymy, że $\Gamma$ nie ma punktów osobliwych, a zatem jest krzywą nieosobliwą, to jej rodzaj definiuje się wzorem

g($$\Gamma$$) = $${\frac{{1}}{{2}}}$$(n - 1)(n - 2)

gdzie n jest stopniem wielomianu f. Hipoteza Mordella - czy raczej twierdzenie Faltingsa - orzeka, iż:

Twierdzenie: Jeśli wielomian f ma współczynniki wymierne, krzywa $\Gamma$ jest nieosobliwa oraz g($\Gamma$) $\geq$ 2, to na $\Gamma$ leży jedynie skończenie wiele punktów o współrzędnych wymiernych.

Liczby wymierne można tu zastąpić dowolnym ciałem liczbowym.

Ponieważ rozważana w FLT krzywa jest nieosobliwa i dla n $\geq$ 4 jej rodzaj jest równy co najmniej 2, można do niej zastosować wynik Faltingsa. Niestety, żaden ze znanych obecnie dowodów twierdzenia Faltingsa nie daje efektywnej metody wyznaczenia punktów wymiernych na krzywej. Wszelako Parsin pokazał (stosując metody Mumforda i Arakelova), że dowód Faltingsa daje oszacowanie liczby takich punktów.

* * *

W latach 70-tych zauważono (Y. Hellegouarch, "Courbes elliptiques et équations de Fermat", Besançon, These 1972, G. Frey, "Rationale punkten auf Fermatkurven and getwisten Modulkurven", Crelle's Journal Reine Angew. Math. 331(1982), 185-191), że zaprzeczenie FLT ma dość dziwne konsekwencje w klasycznej dziedzinie matematyki - w teorii krzywych eliptycznych. Aby wyjaśnić bliżej te pojęcia musimy przytoczyć podstawowe fakty z teorii krzywych eliptycznych, form modułowych i reprezentacji Galois ciała $\mathbb {A}$.

Niech G będzie grupą Galois rozszerzenia $\mathbb {A}$ $\supset$ $\mathbb {Q}$, tj. grupą wszystkich $\mathbb {Q}$-automorfizmów ciała $\mathbb {A}$. W grupie G wprowadzamy tzw. topologię Krulla w następujący sposób: za bazę otoczeń jedności przyjmujemy rodzinę grup Galois rozszerzeń $\mathbb {A}$ $\supset$ K, gdzie K przebiega wszystkie skończone rozszerzenia $\mathbb {Q}$. W tej topologii G jest zwartą grupą topologiczną, zaś zasadnicze twierdzenia teorii Galois mają następujący, intuicyjnie jasny odpowiednik: istnieje wzajemnie jednoznaczne przyporządkowanie pomiędzy podciałami ciała $\mathbb {A}$ a domkniętymi podgrupami H $\subset$ G, dana wzorem:

H $$\mapsto$$ $$\mathbb {A}$$^H = {a $$\in$$ $$\mathbb {A}$$ : $$\forall_{{h \in H}}^{}$$h(a) = a}.

Potrzebna nam będzie też informacja, że dla każdej liczby pierwszej l istnieje w G pewna klasa elementów sprzężonych (tzw. automorfizmy Frobeniusa), złożona z wszystkich elementów g $\in$ G o następującej własności: jeśli l jest nierozgałęziona w rozszerzeniu K $\supset$ $\mathbb {Q}$ (tj. ideał generowany przez l w pierścieniu liczb całkowitych ciała K nie jest zawarty w kwadracie żadnego ideału maksymalnego tego pierścienia), zaś $\mathfrak{M}$ jest dowolnym ideałem maksymalnym pierścienia $\mathbb {Z}$_K liczb całkowitych ciała K, który zawiera l, to dla wszystkich x $\in$ $\mathbb {Z}$_K mamy:

g(x) - x^l $$\in$$ $$\mathfrak{M}$$.

Przez Frob_l oznaczać będziemy dowolny automorfizm Frobeniusa odpowiadający liczbie l.

* * *

Przejdziemy teraz do krzywych eliptycznych i rozpoczniemy od klasycznego przypadku krzywych zdefiniowanych nad ciałem liczb zespolonych. Krzywą eliptyczną będziemy nazywać nieosobliwą krzywą E $\subset$ $\mathbb {C}$² o równaniu

Y² = f (X),

gdzie f jest wielomianem trzeciego stopnia o współczynnikach zespolonych. Łatwo zauważyć, że w tym przypadku nieosobliwość oznacza, że wielomian f nie ma pierwiastków wielokrotnych. Przez nieosobliwe przekształcenie liniowe można każdą taką krzywą sprowadzić do postaci:

Y² = 4X³ + aX + b

przy czym a, b $\in$ $\mathbb {C}$. Jest to tzw. postać Weierstrassa krzywej eliptycznej. Do tak zdefiniowanej krzywej dołącza się na ogół punkt w nieskończoności, otrzymując tym samym krzywą zwartą na płaszczyźnie rzutowej.

Z klasycznej teorii funkcji eliptycznych wynika istnienie liniowo niezalażnych nad $\mathbb {R}$ liczb zespolonych $\omega_{1}^{}$,$\omega_{2}^{}$ takich, że jeśli $\Lambda$ = $\mathbb {Z}$$\omega_{1}^{}$ $\oplus$ $\mathbb {Z}$$\omega_{2}^{}$ $\subset$ $\mathbb {C}$² jest generowaną przez nie grupą addytywną, to związana z nią funkcja Weierstrassa:

$$\wp$$(z) = $${\frac{{1}}{{z^2}}}$$ + $$\sum_{{0 \neq \omega \in \Lambda}}^{}$$($${\frac{{1}}{{(z - \omega)^2}}}$$ - $${\frac{{1}}{{\omega^2}}}$$)

spełnia równanie różniczkowe:

$$\wp{^\prime}$$(z)² = 4$$\wp$$(z)³ + a$$\wp$$(z) + b,

a zatem dla dowolnego z $\in$ $\mathbb {C}$ $\setminus$ $\Lambda$ punkt P(z) = ($\wp$(z),$\wp{^\prime}$(z)) leży na E. Funkcja $\wp$(z) jest dwuokresowa z okresami podatawowymi $\omega_{1}^{}$ i $\omega_{2}^{}$, a więc można ją traktować jak funkcję określoną na grupie ilorazowej $\mathbb {C}$/$\Lambda$. Nietrudno sprawdzić, że układ

$$\wp$$(z) = z₁,    $$\wp{^\prime}$$(z) = z₂

ma przy dowolnych z₁, z₂ dokładnie jedno rozwiązanie z $\in$ $\mathbb {C}$/$\Lambda$, przeto odwzorowanie $\mathbb {C}$/$\Lambda$ $\rightarrow$ E dane przez z $\mapsto$ P(z) jest wzajemnie jednoznaczne.

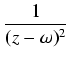Odwzorowanie to pozwala przenieść strukturę grupy abelowej z $\mathbb {C}$/$\Lambda$ na E. Grupa ta jest izomorficzna z torusem $\mathbb {R}$/$\mathbb {Z}$ $\oplus$ $\mathbb {R}$/$\mathbb {Z}$, a więc jej podgrupa torsyjna E_tor, złożona z elementów rzędu skończonego, jest sumą prostą 2 egzemplarzy podgrupy torsyjnej grupy $\mathbb {R}$/$\mathbb {Z}$. Ponieważ $\mathbb {R}$/$\mathbb {Z}$ jest izomorficzna z multyplikatywną grupą liczb zespolonych o module 1, jej podgrupa torsyjna jest izomorficzna z grupą wszystkich pierwiastków z jedności, a stąd w szczególności podgrupa E_N grupy E złożona z elementów x $\in$ E spełniających Nx = 0 jest dla każdego naturalnego N izomorficzna z C_N $\oplus$ C_N.

Działanie na krzywej eliptycznej można wyrazić przez współrzędne, używając funkcji wymiernych. Pozwala to (po dodaniu punktu w nieskończoności) na wprowadzenie struktury grupy abelowej na zbiorach E = $\Gamma$ $\cup$ {$\infty$}, gdzie $\Gamma$ jest nieosobliwą krzywą w k² (gdzie k oznacza dowolne ciało), zdefiniowaną przez równanie postaci:

Y² + a₁XY + a₃Y = X³ + a₂X² + a₄X + a₆,    a_i $$\in$$ k,

gdzie $\infty$ jest zerem E. W przypadku ciał o charakterystyce różnej od 2 i od 3, równanie to łatwo sprowadzić do równania w postaci Weierstrassa.

Ograniczymy się teraz do krzywych określonych przez równanie o współczynnikach wymiernych. Niech zatem E $\subset$ $\mathbb {C}$² $\cup$ {$\infty$} będzie taką krzywą, zadaną równaniem w powyższej postaci. Zdefiniujmy wyróżnik krzywej wzorem:

$$\Delta$$(E) = 0b₂b₄b₆ -27b₆² -8b₄³ - b₂²b₈

gdzie:

b₂ = a₁² +4a₂,

b₄ = a₁a₃ +2a₄,

b₆ = a₃² +4a₆,

b₈ = (b₂b₆ - b₄²)/4.

W przypadku, gdy E jest dana równaniem weierstrassowskim, nietrudno dostrzec związek $\Delta$(E) z wyróżnikiem wielomianu f. Odnotujmy też fakt, że nieco dziwaczna numeracja współczynników występujących w powyższych wzorach nie jest fanaberią autora, ale wynika z uwarunkowań historycznych i jest powszechnie przyjęta w literaturze.

Niech teraz l będzie liczbą pierwszą. Załóżmy, że sprowadziliśmy już naszą krzywą do postaci weierstrassowskiej (przypadek, w którym nie jest to możliwe - ze względu na ograniczoną objętość tego artykułu - pomijamy) i rozważamy ją jako krzywą rzutową, a więc krzywą E daną równaniem:

Y²Z = X³ + aXZ² + bZ³,

gdzie a, b $\in$ $\mathbb {Q}$ oraz - jak wcześniej wspomnieliśmy:

$$\Delta$$(E) = 4a³ +27b² $$\neq$$ 0.

Z pewnych względów, o których nie będziemy tu pisać, "poprawiliśmy" tu postać Weierstrassa tak, aby pozbyć się w niej współczynnika 4. Dokonujemy zmiany współrzędnych X $\mapsto$ X/c², Y $\mapsto$ Y/c³, gdzie c jest dobrane w ten sposób, aby ,,nowe współczynniki'' a i b były całkowite, a wartość bezwzględna |$\Delta$| była możliwie najmniejsza. Tak przerobioną krzywą nazywamy krzywą w postaci minimalnej (albo modelem minimalnym krzywej). Jeżeli teraz w postaci minimalnej krzywej współczynniki a i b zastąpimy ich obrazami w ciele $\mathbb {F}$_l, to tak otrzymane równanie E^(l) nazwiemy redukcją krzywej E modulo l. Rozróżniamy trzy przypadki:

• Redukcja dobra (good reduction). Jeżeli otrzymana krzywa (nad ciałem skończonym) jest nieosobliwa.

• Redukcja addytywna (additive reduction, cuspidal reduction). Otrzymana krzywa (nad ciałem skończonym) ma osobliwość - szpic (cusp). Można pokazać, że jest tak (w przypadku, gdy l $\neq$ 2, 3) gdy l| 4a³ +27b² oraz l| - 2ab.

• Redukcja multyplikatywna (multiplicative reduction, nodal reduction). Otrzymana krzywa (nad ciałem skończonym) ma osobliwość - węzeł (node). Można pokazać, że jest tak (w przypadku gdy l $\neq$ 2, 3) gdy l| 4a³ +27b² oraz p nie dzieli -2ab.

Redukcje addytywne i multyplikatywne nazywamy złymi redukcjami. Konduktor (przewodnik) definiujemy jako liczbę:

N_e = $$\prod_{l}^{}$$l^f_l

gdzie iloczyn przebiega po tych liczbach l, dla których krzywa ma złą redukcję, zaś wykładnik f_l jest zdefiniowany następująco:

f_l = 1 gdy E ma redukcję multyplikatywną dla l
f_l $\geq$ 2 gdy E ma redukcję addytywną dla l

Dokładniej, wartość f_l można wyliczyć z tzw. wzoru Ogg'a:

f_l = ord_l($$\Delta$$(E)) + 1 - m_l

gdzie ord_l oznacza wykładnik l-adyczny, $\Delta$(E) jest wyróżnikiem postaci minimalnej krzywej a m_l... jest liczbą składowych nierozkładalnych w modelu Nerona krzywej E. Czytelnika zainteresowanego bardziej precyzyjną definicją odsyłamy do podręczników - na przykład do ksiązki Hussemollera "Elliptic Curves".

Jeśli dla każdej liczby pierwszej krzywa E ma redukcję dobrą lub multyplikatywną, to mówimy, że jest to krzywa semistabilna.

* * *

Z tego, że równanie E ma współczynniki wymierne, wynika z łatwością, że współrzędne elementów rzędu skończonego grupy E są liczbami algebraicznymi i że grupa Galois G rozszerzenia $\mathbb {A}$/$\mathbb {Q}$ działa na grupie E_tor wszystkich takich elementów jak grupa automorfizmów. Przy tym grupy E_N $\subset$ E_tor są niezmiennicze, tj. dla dowolnego automorfizmu $\sigma$ $\in$ G mamy:

$$\sigma$$(E_N) = E_N.

Niech teraz p będzie nieparzystą liczbą pierwszą, dla której krzywa eliptyczna ma dobrą redukcję i rozważmy ciąg grup

E_p $$\subset$$ E_p² $$\subset$$...$$\subset$$ E_pⁿ $$\subset$$...

wraz z homomorfizmami E_pⁿ $\rightarrow$ E_p^n-1 wyznaczonymi przez mnożenie przez p. Otrzymujemy w ten sposób granicę odwrotną T_P(E) grup E_pⁿ. Iloczyn tensorowy V_p(E) = T_P(E) $\oplus_{{{\mathbb Z}_p}}^{}$ $\mathbb {Q}$_p, nazywa się modułem Tate'a krzywej E. Ponieważ grupa E_p^k jest izomorficzna z C_p^k $\oplus$ C_p^k, działanie $\sigma$ $\in$ G na E_p^k można opisać za pomocą pewnej macierzy z GL₂($\mathbb {Z}$/p^k$\mathbb {Z}$). Tym samym każdemu elementowi $\sigma$ $\in$ G daje się przyporządkować pewną macierz - przyporządkowanie takie jest homomorfizmem, a więc otrzymujemy rodzinę dwuwymiarowych reprezentacji nad pierścieniami reszt modp^k:

$$\phi_{{p^k}}^{}$$ : G $$\rightarrow$$ GL₂($$\mathbb {Z}$$/p^k$$\mathbb {Z}$$).

Nietrudno spostrzec, że odwzorowanie $\phi_{{p^k}}^{}$ jest ciągłe, a gdy k₁ $\geq$ k₂, to ponadto:

$$\phi_{{p^{k_1}}}^{}$$($$\sigma$$)modp^k₂ = $$\phi_{{p^{k_2}}}^{}$$($$\sigma$$)

dla dowolnego $\sigma$ $\in$ G. Ostatni warunek pokazuje, że grupa G działa na V_p jako grupa automorfizmów, przy czym grupę V_p traktujemy tu jak $\mathbb {Z}$_p-moduł. W ten sposób otrzymujemy ciągła reprezentację:

$$\pi_{p}^{}$$ : G $$\rightarrow$$ GL₂($$\mathbb {Z}$$_p),

która - złożona z redukcją modp - daje reprezentację:

$$\phi_{p}^{}$$ : G $$\rightarrow$$ GL₂($$\mathbb {F}$$_p).

* * *

Oznaczmy teraz przez E($\mathbb {Q}$) zbiór punktów krzywej E o współrzędnych wymiernych. Okazuje się (nie jest to trudne w dowodzie), że jest to podgrupa grupy E. Słynne twierdzenie Mordella z 1922 roku stwierdza, że grupa E($\mathbb {Q}$) jest postaci F $\oplus$ Z^r, gdzie r $\geq$ 0, zaś F jest grupą skończoną. O ile struktura grupy F jest dobrze znana, o tyle wielkość r pozostaje nadal tajemnicza. Nie wiadomo, na przykład, czy liczba ta może być dowolnie duża. Barry Mazur (matematyk amerykański, którego rodzice pochodzili z Galicji) pokazał w 1976 roku, że grupa E($\mathbb {Q}$) jest cykliczna rzędu m przy m $\leq$ 10 lub m = 12, lub też jest postaci C₂ $\oplus$ C_2m dla m $\leq$ 4. W szczególności nie zawiera ona elementów rzędu p, gdy p jest liczbą pierwszą większą od 7.

* * *

W zastosowaniu do twierdzenia Fermata fundamentalna rolę odgrywają krzywe eliptyczne E zdefiniowane równaniem postaci:

Y² = X(X - A)(X + B),

gdzie A, B są liczbami całkowitymi, przy czym A $\equiv$ 1(mod4) oraz B $\equiv$ 0(mod2⁵). Łatwo się przekonać, iż dla nieparzystych liczb pierwszych l krzywa E ma dobrą redukcję wtedy i tylko wtedy, gdy l nie dzieli AB(A + B), a jeśli warunek ten nie jest spełniony, to redukcja jest multyplikatywna. W przypadku l = 2 okazuje się także, że otrzymujemy redukcję multyplikatywną, a zatem krzywa jest semistabilna. Zobaczymy za chwilę, jak fakt ten decyduje o skuteczności pomysłu wykorzystania krzywych eliptycznych do dowodu FLT.

Przydatność opisywanych krzywych do zagadnienia Fermata zauważył Frey. W arytmetycznej geometrii algebraicznej znana jest nierówność Bogomołowa-Miyaoki-Yau wiążąca pewne niezmienniki krzywej określonej nad liczbami całkowitymi. Gdyby udało się wzmocnić nierówność Bogomołowa dla powierzchni arytmetycznych, to ze wzmocnionej nierówności wynikałaby (za pomocą twierdzenia Parsina) hipoteza Szpiro, o związku między minimalnym wyróżnikiem i konduktorem krzywej eliptycznej. Hipoteza ta, postawiona w 1982 roku, głosi w przypadku krzywych eliptycznych E zdefiniowanych nad ciałem liczb wymiernych, że dla każdego $\epsilon$ > 0 mamy:

$$\Delta$$(E) $$\leq$$ C($$\epsilon$$)N_E^6+$\epsilon$.

Z hipotezy Szpiro wynika, że FLT zachodzi dla prawie wszystkich wykładników pierwszych. W 1988 na wykładzie w Bonn Miyaoka ogłosił, że udało mu się wzmocnić nierówność Bogomołowa, ale jego dowód okazał się błędny. Jak pokazał Masser w 1990 roku, w powyższej nierówności nie można zastąpić wykładnika 6 przez mniejszą liczbę. Interesujące wnioski z hipotezy Szpiro podane są w książce Vojty (P. Vojta, "Diophantine approximations and value distribution theory", Lecture Notes in Mathematics 1239, Springer 1987). Z tejże pozycji dowiedzieć się można także o tzw. hipotezie Vojty o wysokościach względem klasy kanonicznej punktów na krzywych określonych nad pierścieniem $\mathbb {Z}$ liczb całkowitych, z której wynika i hipoteza Mordella, i FLT dla prawie wszystkich wykładników n.

Odnotujmy tu - dla dalszych potrzeb - że w przypadku omawianych krzywych konduktor równy jest AB(A + B).

* * *

Podamy teraz kilka informacji o formach parabolicznych. Oznaczmy przez $\Gamma$ grupę macierzy dwuwymiarowych o wyznaczniku równym jedności i współczynnikach całkowitych. Niech N będzie liczbą naturalną i niech

$$\Gamma_{0}^{}$$(N) = $$\left\{\vphantom{ \left[ \begin{array}{cc} a & b c & d \end{array} \right] \in \Gamma: N \vert c}\right.$$$$\left[\vphantom{ \begin{array}{cc} a & b c & d \end{array} }\right.$$$$\begin{array}{cc} a & b \\ c & d \end{array}$$$$\left.\vphantom{ \begin{array}{cc} a & b c & d \end{array} }\right]$$ $$\in$$ $$\Gamma$$ : N| c$$\left.\vphantom{ \left[ \begin{array}{cc} a & b c & d \end{array} \right] \in \Gamma: N \vert c}\right\}$$.

Niech $\mathcal {H}$ oznacza górną półpłaszczyznę zespoloną i niech k $\geq$ 2. Funkcję F regularną na $\mathcal {H}$ nazwiemy formą paraboliczną typu (N, k) (cusp form, Spitzenform, forme parabolique), jeśli:

1. F(z) jest przedstawialna jako suma szeregu
   F(z) = $$\sum_{{n=1}}^{{\infty}}$$A_nqⁿ
   dla wszelkich z $\in$ $\mathcal {H}$, gdzie q = e^2$\pi$iz;
2. Dla każdej macierzy $\gamma$ = $\left[\vphantom{ \begin{array}{cc} a & b c & d \end{array} }\right.$$\begin{array}{cc} a & b c & d \end{array}$$\left.\vphantom{ \begin{array}{cc} a & b c & d \end{array} }\right]$ $\in$ $\Gamma$ funkcja
   (cz + d )^-kF($${\frac{{az + b}}{{cz + d}}}$$)
   da się przedstawić w postaci szeregu:
   $$\sum_{{n=1}}^{{\infty}}$$A_n($$\gamma$$)e^{${\frac{{2 \pi i n z}}{{N}}}$};

3. Dla z $\in$ $\mathbb {H}$ i dla każdej macierzy $\left[\vphantom{ \begin{array}{cc} a & b c & d \end{array} }\right.$$\begin{array}{cc} a & b c & d \end{array}$$\left.\vphantom{ \begin{array}{cc} a & b c & d \end{array} }\right]$ $\in$ $\Gamma_{0}^{}$(N):
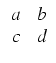
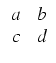
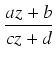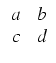
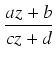   F($${\frac{{az + b}}{{cz + d}}}$$) = (cz + d )^kF(z).

Pierwsze dwa warunki można też zapisać tak: grupa $\Gamma_{0}^{}$(N) działa przez homografie na zbiór $\mathcal {H}$ i ma tam spójny obszar fundamentalny D, który nie jest zwarty, ale który można uzwarcić przez dodanie punktu w nieskończoności oraz skończenie wielu punktów parabolicznych (cusp, Spitzenpunkt), czyli takich punktów rzeczywistych r, dla których istnieje homografia $\gamma$ $\in$ $\Gamma_{0}^{}$(N), w której r jest jedynym punktem stałym (tj. - co łatwo sprawdzić - gdy $\pm$$\gamma$ nie jest macierzą jednostkową, a ślad $\gamma$ jest równy $\pm$2). Bazą otoczeń takiego punktu jest rodzina zbiorów złożonych z r i z wnętrz okręgów leżących w $\mathcal {H}$ i stycznych do prostej rzeczywistej w punkcie r. W ten sposób otrzymujemy zwartą przestrzeń topologiczną X₀(N) o pewnych własnościach analitycznych. Pierwsze dwa warunki orzekają więc, że funkcja F(z) przedłuża się w sposób ciągły na X₀(N) i jest równa zeru w każdym punkcie zbioru X₀(N) $\setminus$ D.

Zbiór S(N, 2) form parabolicznych typu (N, 2) jest przestrzenią liniową nad ciałem liczb zespolonych i - jak obliczył Shimura w 1971 roku:

dim_{$\mathbb {C}$}S(2, 2) = 0.

* * *

W przestrzeni form parabolicznych S(2, 2) działa rodzina

{T_p : p - pierwsze , p$$\nmid$$N} $$\cup$$ {U_p : p - pierwsze , p| N}

tzw. operatorów Heckego, zdefiniowanych dla form danych powyższymi wzorami przez

T_p(F) = $$\sum_{n}^{}$$A_pnqⁿ + p$$\sum_{n}^{}$$A_nq^pn

oraz

U_p(F) = $$\sum_{n}^{}$$A_pnqⁿ.

Niech teraz f będzie taką niezerową formą paraboliczną typu (N, 2), dla której A₁ = 1 i która jest wektorem własnym dla wszystkich operatorów Heckego T_p. Załóżmy ponadto, że wszystkie współczynniki A_n są całkowite. Znany wynik Deligne z 1974 roku stwierdza, że istnieje wtedy ciągła reprezentacja

$$\rho_{f}^{}$$ : G $$\rightarrow$$ GL₂($$\mathbb {Z}$$_p)

grupy G, która spełnia następujące warunki:

• jest półprosta;
• jeśli l$\nmid$pN, to ślad macierzy $\rho_{f}^{}$(Frob_l) równy jest współczynnikowi a_l, a jej wyznacznik równa się l.

Każdą taką reprezentację nazywamy reprezentacją modułową. Jeżeli zastąpimy elementy macierzy reprezentacji modułowej $\rho_{f}^{}$ przez ich reszty modp, to otrzymamy nową reprezentację R_p nad ciałem p-elementowym $\mathbb {F}$_p.

Słynna hipoteza Taniyamy-Weila orzeka, że jeśli E jest krzywą eliptyczną, l jest liczbą pierwszą, a reprezentacja $\pi_{l}^{}$ opisana wcześniej jest nieprzywiedlna, to jest ona reprezentacją modułową, odpowiadającą pewnej formie parabolicznej typu (N, 2), gdzie N jest konduktorem krzywej E, przy czym forma ta nie zależy od l. Krzywe, dla których zachodzi hipoteza Taniyamy-Weila nazywamy krzywymi modułowymi.

* * *

Wyjaśnimy teraz, jak opisane pojęcia wiążą się z twierdzeniem Fermata.

Niech X = a, Y = b, Z = c będą liczbami naturalnymi, bez wspólnego dzielnika większego od 1, dla których spełnione jest równanie:

X^p + Y^p + Z^p = 0,

przy czym p $\geq$ 5. Zamieniając ewentualnie liczby kolejnością możemy założyć, że a $\equiv$ 1(mod4) oraz b $\equiv$ 0(mod2). Niech E_p(a, b, c) będzie krzywą eliptyczną o równaniu:

y² = z(x - a^p)(x + b^p).

Jej konduktor równy jest iloczynowi liczb pierwszych dzielących abc.

Twierdzenie: Krzywe E_p(a, b, c) nie są krzywymi modułowymi.

Szkic dowodu: Załóżmy, że krzywa taka jest modułowa i niech reprezentacja $\phi_{p}^{}$ będzie zadana wzorem

$$\phi_{p}^{}$$ : G $$\rightarrow$$ GL₂($$\mathbb {F}$$_p).

opisanym szczegółowo powyżej. W 1987 roku Serre pokazał, że jej przywiedlność prowadziłaby do istnienia krzywej eliptycznej mającej punkt rzędu p o współrzędnych wymiernych, co nie jest możliwe dla p > 7 w świetle twierdzenia Mazura. Istnieje zatem forma paraboliczna F $\in$ S(N, 2) o tej własności, że $\phi_{p}^{}$ pokrywa się z reprezentacją F_p związaną z F. Okazuje się, że istnieją formy paraboliczne o tej samej własności, należące do S(M, 2), gdzie M jest właściwym dzielnikiem N. Mazur i Ribet pokazali w 1990 roku, że jeśli

R_l : G $$\rightarrow$$ GL(2,$$\mathbb {2}$$, F_l)

jest ciągła reprezentacją modułową odpowiadającą pewnej formie parabolicznej f typu (2, N), p jest liczbą pierwszą dzielącą N, a p² nie dzieli N, wówczas przy pewnych technicznych założeniach o R_l, jeśli p $\nequiv$ 1(modl ) lub NWD(l, N) = 1, to istnieje forma paraboliczna w S(2, N/2), której odpowiada ta sama reprezentacja R_l. Spełnienie tych założeń twierdzenia w przypadku nieparzystych liczb pierwszych p i reprezentacji związanej z krzywą E_p(a, b, c) wynika ze wspomnianych prac Serre'a. Teraz widać, że $\rho_{p}^{}$ odpowiada pewnej formie parabolicznej typu (2, 2) i wystarczy sobie przypomnieć, że skoro dim_{$\mathbb {C}$}S(2, 2) = 0, to forma ta musi być zerowa, co nie jest możliwe, gdyż jest ona nietrywialna.

* * *

Ponieważ krzywe E_p(a, b, c) są semistabilne, do dowodu twierdzenia Fermata pozostaje wykazać, że każda semistabilna krzywa musi być modułowa. 23 czerwca 1993 roku światową prasę i Internet obiegła wiadomość, że prof. Andrew Wiles udowodnił Wielkie Twierdzenie Fermata. Na zakończenie cyklu trzech wykładów w ramach warsztatów o teorii Iwasawy, formach automorficznych i reprezentacjach p-adycznych w Instytucie I. Newtona w Cambridge, w Anglii, Wiles ogłosił, że udowodnił hipotezę Shimury-Taniyamy-Weila dla semistabilnych krzywych eliptycznych. Po pewnym czasie okazało się, że dowód zawiera lukę.

In view of the speculation on the status of my work on the Taniyama-Shimura conjecture and Fermat's Last Theorem I will give a brief account of the situation. During the review process a number of problems emerged, most of which have been resolved, but one in particular I have not yet settled. The key reduction of (most cases of) the Taniyama-Shimura conjecture to the calculation of the Selmer group is correct. However the final calculation of a precise upper bound for the Selmer group in the semistabular case (of the symmetric square representation associated to a modular form) is not yet complete as it stands. I believe that I will be able to finish this in the near future using the ideas explained in my Cambridge lectures.

The fact that a lot of work remains to be done on the manuscript makes it still unsuitabular for release as a preprint . In my course in Princeton beginning in February I will give a full account of this work.

Andrew Wiles.

W 1995 roku ukazały się dwa artykuły (A. Wiles, "Modular Elliptic Curves and Fermat's Last Theorem", Annals of Mathematics 141(1995) No. 3, str. 443-551; A. Wiles, R. Taylor, "Ring Theoretic Properties of Certain Hecke Algebras", Annals of Mathematics 141 (1995) No. 3, str. 553-572), datowane na 7 października 1994, zawierające poprawiony dowód hipotezy Shimury-Taniyamy-Weila (drugi z nich podaje nowy dowód tego, co w 1993 było luką w dowodzie). Wielkie Twierdzenie Fermata zostało tym samym udowodnione.